双摆臂履带式移动机器人侧倾稳定性分析
杨忠炯,江艳蕊,周立强
(1.中南大学 机电工程学院,长沙 410083;2.中南大学 高性能复杂制造国家重点实验室,长沙 410083)
0 引言
移动机器人的诞生是为了代替人类完成某些特定的任务,例如进入废墟等狭小的空间寻找生命、灾后矿山环境探测、排爆等[1]。常见的移动机器人有足式、轮式、履带式等,而在未知环境中执行任务的时候,地面环境通常是非平整的,履带式移动机器人因其良好的地面适应能力被广泛应用于地形条件比较复杂的地方[2~4],如日本千叶大学研制的“木槿”机器人在地震废墟中执行搜救任务,美国Warwick大学研制的“warwick”机器人被用来执行城市搜救任务。由于履带式移动机器人工作环境较为复杂,虽然自身具有良好的稳定性,但在废墟、矿山、战场等恶劣环境中也会存在失稳的情况,机器人的摆臂运动对车身稳定性的影响直接关系到机器人能否实现越障[5]。现如今已有不少研究者对关节式履带机器人在某些经典地形的越障性能和动作规划做了相关研究[6~8],但是这些研究中对障碍的模拟都局限于爬楼梯、跨越沟壕两种经典障碍,这两种障碍的分析都是在满足机器人仰俯稳定性的情况下进行的,然而为了保证机器人的行走特性,机器人结构设计时其长度往往大于宽度,因此机器人的侧倾稳定裕度明显低于机器人的仰俯稳定裕度。因此,在研究机器人姿态控制时,机器人的侧倾稳定性也是不可忽略的一个重要因素[9]。而且对机器人爬越台阶和沟壑的分析都是建立在机器人左右履带同时越过同样障碍的前提下,但机器人在实际运行时左右履带的状态往往不会处于相同的状态,即障碍在机器人的一侧[10],所以单纯的仰俯地形无法充分反应实际的复杂地形,其研究结果存在一定局限性。
本文着重研究双摆臂履带式移动机器人在左右高低不平的地面上运行时的状况,以单侧台阶为例,首先对摆臂系统收起时的普通双履带移动机器人进行稳定性判定,然后对摆臂系统工作时的机器人进行稳定性分析,得出静态稳定性条件[11],建立摆臂系统和机器人姿态的联系,再结合摆臂系统对机器人姿态的影响设计了在侧倾情况下的自主越障规划。研究表明:此种越障控制,可以增大双摆臂履带式移动机器人在左右不平道路上的运动平稳性能。
1 双摆臂履带式移动机器人机械结构设计
本文的研究对象为双摆臂履带式移动机器人,在没有障碍的情况下,摆臂收回状态如图1所示,此种状态机器人的几何尺寸为800×600×254mm,摆臂长度为400mm。

图1 履带式移动机器人结构图
双摆臂履带式移动机器人的行走动力由两条主履带提供,转向系统采取原地转向。为了提高履带式移动机器人的越障性能,在机器人机身上增加了摆臂结构,摆臂系统可以实现360度旋转。通常的双摆臂机器人,两侧摆臂系统均采用一个电机驱动,即双侧摆臂的运动时刻保持一致,但是针对左右不平的地面,采用同一个电机驱动会存在很大的局限性,常常会导致另一侧摆臂支撑点悬空,从而更加不利于机器人的平稳运行,本文中双摆臂履带式移动机器人的摆臂系统采用双电机进行驱动,使得两侧的摆臂系统可以实现旋转不同的角度,从而提高机器人对不同障碍的适应性能。
2 机器人越障规划
本文中采用单侧台阶进行模拟能导致机器人在左右方向上产生侧倾的地形,这也是现有研究中所采用的经典地形之一,现实中所有的复杂地形都是前后不平或左右不平或者由两种状态叠加而成,本文则重点分析机器人在左右不平地形上运行时的运动规划,当机器人在斜坡上运行发生失稳时,需要调节摆臂系统,利用摆臂的支撑作用改变机器人的重心位置。双摆臂履带式移动机器人在斜坡上运行时,并不需要一直启动摆臂系统,当机器人在侧向台阶上稳定运行时,摆臂系统则不需要启动,处于收回状态,即相当于普通双履带式移动机器人行走,如图2(a)所示。机器人在执行任务过程中常常搭载三维扫描仪、摄像头等精密的探测仪器,所以在地形起伏严重的路面上,机器人的重心位置变化幅度较大,往往导致测量误差增大,此时可通过控制摆臂系统使机器人更加平稳的运行;当斜坡角度过大,传感器检测到机器人的侧倾角度越来越大并且有失稳的预兆时,机器人较低侧摆臂系统启动,但是与爬楼梯时状态不同,双摆臂履带式移动机器人在这种斜坡状态下,摆臂旋转方向不能使摆臂向前伸开,而应向后旋转使摆臂撑地,才能使支撑点在机器人中间区域,使机器人处于稳定状态,如图2(b)所示。
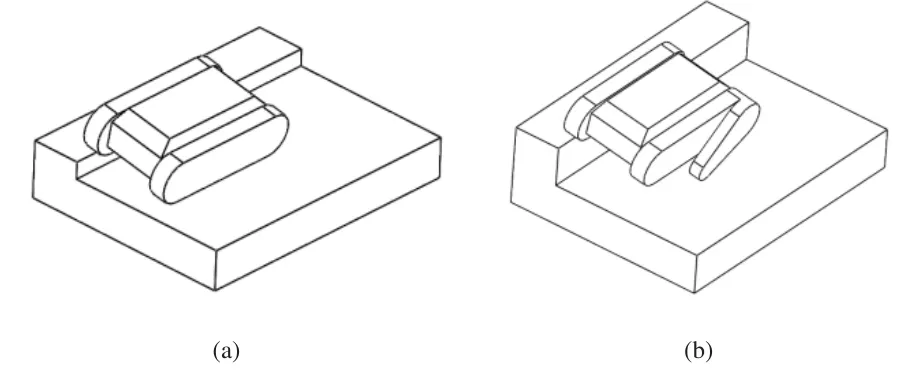
图2 履带式移动机器人斜坡运动规划示意图
3 机器人侧倾稳定性分析
3.1 固定双履带机器人侧倾稳定性分析
在对履带式移动机器人越障过程进行分析时,首先建立如下三点假设:
1)在对机器人进行越障分析时不考虑摆臂履带的宽度,整车宽度记为b;
2)机器人运行的地面为硬质地面;
3)机器人保持低速行驶。
当机器人在斜坡上进行缓慢移动时,对其稳定性的研究主要聚焦在静态稳定性分析上。对于固定双履带移动机器人而言,在斜坡上运行时,其所允许通过的最大斜坡角度与机器人最大横滚角相等,机器人在不发生侧倾时所允许的最大横滚角记为βmax。由图3可知,当重心M的投影在A'B'内时机器人会保持侧向的稳定性,当重心M的投影与接触点B'重合时为机器人发生侧倾的临界条件,此时机器人的最大横滚角为βmax满足:

式中:b为机器人总宽,h为重心到履带底部的高度。

图3 固定双履带机器人侧倾稳定性分析
3.2 单侧摆臂系统启动时稳定性分析
先通过建立稳定锥的方法直观判定机器人的稳定性,建立以重心M为原点的世界坐标系,各接触点A'ED'所构成的三角形为机器人的稳定三角形,空间椎体MA'ED'称为稳定锥,如图4(a)所示,β为机器人的横滚角,ϕ为机器人通过的斜坡角度,θ为摆臂旋转的角度,L为机器人的长度,如图4(b)、图4(c)所示。
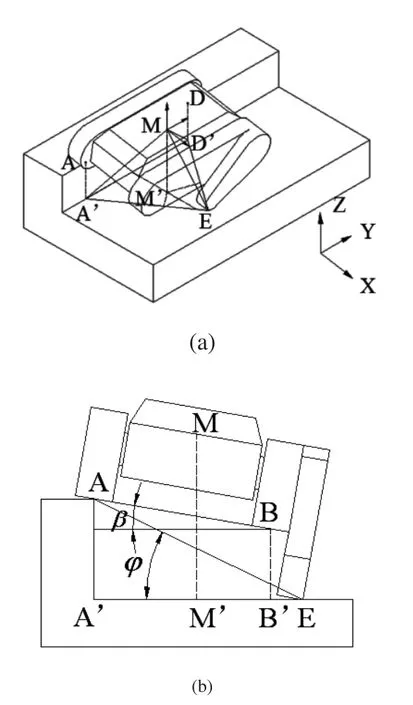

图4 单侧摆臂启动时的稳定性分析
当重心M的投影M'落在稳定三角形内时,则机器人是静态稳定的。由图可知,稳定三角形A'ED'的面积是:

投影三角形A'M'D'、三角形D'M'E'和三角形A'M'E的面积分别是:

以上建立稳定锥的方法可直观的表达机器人的稳定状态,但对机器人稳定性的控制需要对其进行量化计算,所以继而提出侧倾稳定裕度的方法。稳定裕度即机器人重心的投影到稳定三角形各边的最小距离,因本文只对机器人的侧倾稳定性进行分析,所以如图5所示,本文的侧倾稳定裕度为Xr=min{X1,X3}。由于所以X2可忽略不计。
对应的,可先求出稳定三角形三条边在水平面投影的方程为:
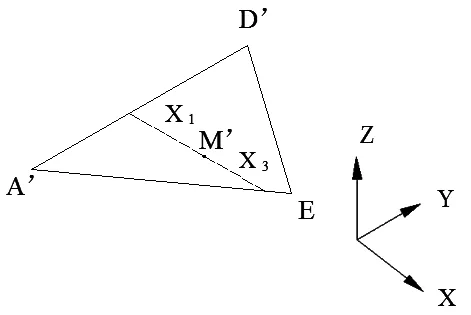
图5 侧倾稳定裕度示意图

其中A'坐标为:
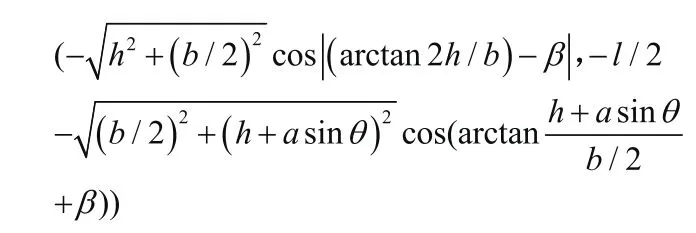
令:
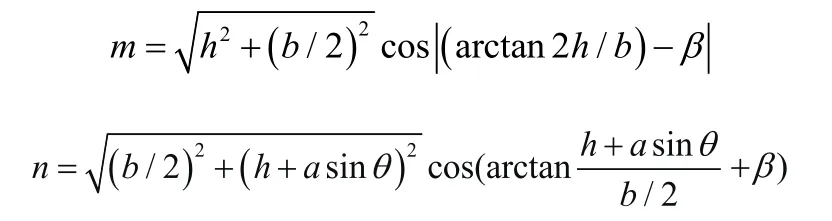
则A'的坐标记为(-m,-l/2-n);D'的坐标为(-m,-l/2-n);E的坐标为(-m,-l/2-a cosθ-n); M'的坐标为(0,0-n);将各点坐标带入方程可求出ai,bi,ci的值,从而求出稳定三角形三条边的方程。M'到各条边投影的距离是:
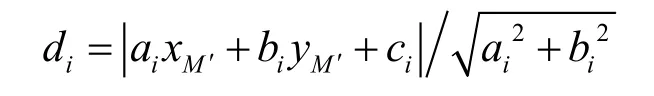
由图可知:
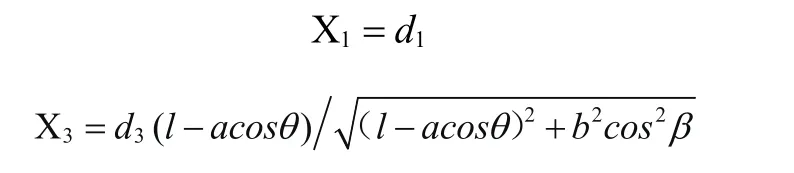
4 摆臂尺寸和摆臂角度对机器人侧倾稳定性的影响分析
由上节中机器人的侧倾稳定裕度可得:

当X3=0时机器人处于临界失稳状态,即机器人的横滚角达到最大值βmax,即:

机器人上方要搭载机械臂,所以重心高度为h=300mm,将各几何尺寸代入式中,可得出摆臂角度与所允许的最大横滚角的关系如图6所示。
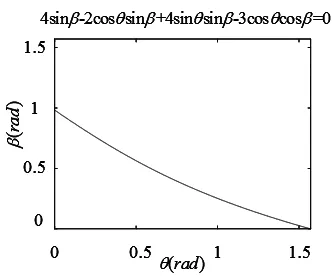
图6 摆臂角度与所允许的最大横滚角的关系图
5 结论
本文对双摆臂履带式机器人在斜坡行驶时进行了动作规划,分别用重心投影法和稳定裕度法分析了固定双履带机器人的稳定性以及启动单侧摆臂系统时的稳定性,重点研究了摆臂角度与机器人所允许的最大横滚角之间的关系,确定了机器人在斜坡运行时的越障性能。经研究可得出如下结论:
1)得出了双摆臂履带式移动机器人固定双履带和单侧摆臂撑起两种状态下的静态稳定条件,确定了相关约束条件。
2)双摆臂履带式移动机器人所允许的最大横滚角会随着机器人摆臂角度的增大而减小,依据机器人不同摆臂角度下的最大横滚角,约束控制机器人的越障,提高了机器人的越障稳定性。

