CoreXY机构3D打印机运动控制算法研究
(河北工业大学 机械工程学院 机械工程系,天津 300130)
0 引言
近年来3D打印机、激光雕刻机、激光切割机以及激光打标机等智能设备兴起,引发了科技爱好者的兴趣。CoreXY机构是广泛应用于这些设备中的机构之一,CoreXY结构相对紧凑,同样体积的情况下,可以实现相对较大的打印尺寸;对于CoreXY结构,在XY平面内运动的两个电机都固定,降低了运动部件的重量,这样也就降低了运动部件的惯性,同样驱动力的情况下,加速度更高,带来的效果就是运动更加敏捷。相对于笛卡尔直角坐标机构、Delta机构[1],CoreXY机构具有明显的优势。为了更加高效精确的控制它,目前比较流行的是广泛用于数控机床控制的插补算法,常用的插补算法有逐点比较法、最小偏差法、Bresenham直线生成算法(计算机图形学中绘制直线的一种经典算法[2])等。这些算法的优点是算法简单、插补计算速度快、插补误差较小,但同时也存在如下缺点:1)不能两轴联动,影响加工精度;2)插补次数多,执行时间长,影响生产效率[3]。所以为了提高机构的执行效率和加工精度,引入一种高精度高效率的算法尤为重要。
熔融沉积成型(Fused Deposition Modeling,FDM)是将丝状的热熔性材料加热融化,同时三维挤出机构在计算机的控制下,根据截面轮廓信息,将材料选择性地涂敷在工作台上,快速冷却后形成一层截面。一层成型完成后,机器工作台下降一个高度(即分层厚度)再成型下一层,直至形成整个实体造型[4]。对于CoreXY 结构的FDM型3D打印机来说,为了快速的打印出高精度的产品模型,需要对打印机的X轴、Y轴、Z轴以及E轴(挤出机构)的联动控制,四者密切配合运动、缺一不可。尤其是X、Y平面的运动对一台3D打印机的打印质量尤为重要;因此实现对平面机构的控制成为3D打印的核心。本文着重论述CoreXY平面机构的运动控制,Z轴和E轴的运动控制相对较为简单,不再详细论述。目前一些主流的3D打印机固件不开源、国内外相关研究资料较少,算法改进与移植困难,这给我们的研究带来困难。本文将数控技术应用于3D打印行业,这将会大大方便3D打印爱好者的开发,同时也降低了入门难度。CoreXY结构3D打印机由于其独特的传动方式,以及其较其他机构的鲜明优势,这种机构的应用前景将不可限量。
为了更准确高效地实现对CoreXY机构的运动控制,本文对CoreXY结构所独有的X、Y平面机构进行运动特性分析,将该机构与典型的直角坐标机构建立一定的数学转化关系,引入了一种比最小偏差法更优的算法。
1 机构特点与运动分析
CoreXY机构最大特点是步进电机都固定在机架一侧,无论运动机构沿X轴还是沿Y轴向运动,两个步进电机都不会随着机构运动,因此减轻了机器在运动过程中的负担,使运动机构的动作更加平稳。CoreXY机构的原理图如图1所示。整个机构的各种运动方式都是通过一根皮带的传动来实现的,这种传动方式可以有效减轻振动,且避免了安装丝杠、移动步进电机的负担,使整体结构更加简单,运动更加灵活,能够在一定程度上提高机构的工作效率。
机构运动位移ΔX,ΔY与步进电机M1、M2的线位移ΔA、ΔB之间的关系如式(1)和(2)所示:

解方程组可得:
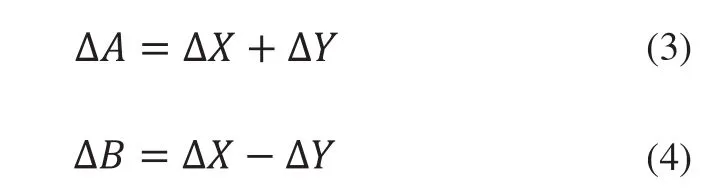
上式中:ΔX、ΔY 分别为3D打印机工料挤出机构所在的滑块分别沿X正方向和沿Y正方向的位移,ΔA、ΔB分别为步进电机M1、M2的线位移,为了方便以顺时针为负、逆时针为正来标记ΔA、ΔB的方向。
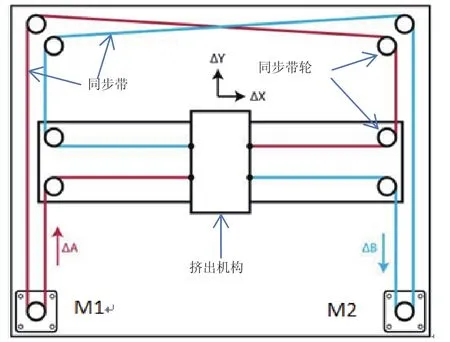
图1 CoreXY 机构传动原理示意图
当步进电机M1和M2以相同的速度顺时针或逆时针同向转动时,机构的滑块就会沿X轴方向水平运动,ΔA、ΔB的大小、方向相同;此时有:
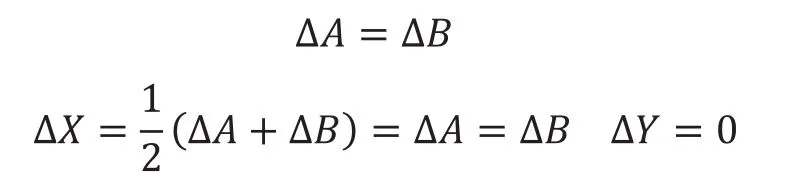
当步进电机M1和M2以相同的速度、相反的方向转动时,机构的滑块就会沿Y轴方向运动,此时:ΔA、ΔB的大小相同,方向相反;此时:
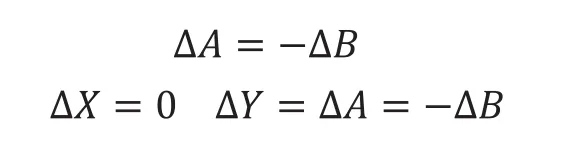
当步进电机M1转动,步进电机M2静止时,滑块将沿着Y=X方向移动;此时:

同理当步进电机M2转动,步进电机M1静止时,滑块将沿着Y=-X方向移动;此时:
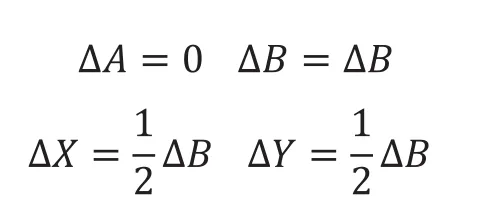
由上可知,CoreXY机构可以非常方便的实现滑块沿着X、Y轴方向和Y=X、Y=-X方向移动,这就为下文的控制算法引入埋下伏笔。
2 运动控制算法研究
2.1 逐点比较法
这里我们先引入逐点比较法,逐点比较法的广泛应用于数控领域,近来随着增材制造和激光加工的兴起,该算法也被应用于FDM型3D打印机的控制中。
要实现3D打印机的连续运动,需要将建立好的三维模型用切片软件进行切片,得到所需打印模型的G代码,代码中存放的是无数层切片的坐标值,要重复这些轨迹,就要实现挤出机构从当前点C(X0,Y0)到目标点D(X1,Y1)的插补运动[5]。
逐点比较法插补过程的每一步都要经过以下四个工作节拍。
1)坐标判断:计算挤出机构的当前位置C(X0,Y0)与目标位置D(X1,Y1)的差值Xe,Ye,并根据Xe,Ye的符号,判断进给方向。
2)坐标进给:根据当前偏差Fn判别的结果,控制机构沿相应的坐标轴进给一步,使挤出机构向模型轮廓靠拢。
3)偏差计算:挤出机构进给一步后,针对新的挤出机构位置,计算新的偏差值Fn+1。
4)终点判别:挤出机构进给一步后,需要判别挤出机构是否已经到达零件轮廓的终点。如果已经到达终点,则停止插补过程,目标位置赋值为当前位置;如果未到达终点,则返回到第1)步,重复上述四个节拍[6]。表1为打印机挤出机构各卦限的运动判断公式。
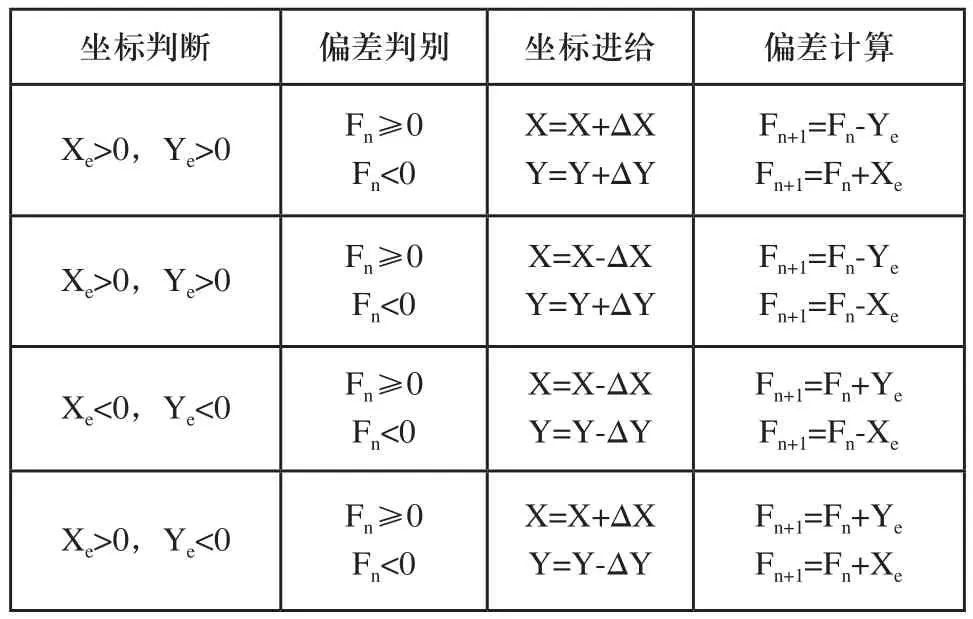
表1 逐点比较法插补公式表
挤出机构在具体卦限的具体进给方向和偏差判断如图2,偏差F≥0时,挤出机构沿着X轴运动,F<0时挤出机构沿着Y轴运动,步进电机M1和M2以相同的速度顺时针或逆时针同向转动时,就可以沿着X轴运动,步进电机M1和M2以相同的速度顺时针或逆时针反向转动时,就可以沿着Y轴运动。不妨假设步进电机的脉冲当量为0.1mm,当前点为C(0,0),目标点为D(0.5,0.7)或D(0.7,0.5),图3为经MATLAB仿真得到逐点比较法的运动效果图,图中的细线代表实际走过轨迹,粗线代表理想轨迹,由图3我们可以明显的看出,从一点到另一点,由于机构只沿着X或Y轴运动存在很大的误差,而且插补效率很低。
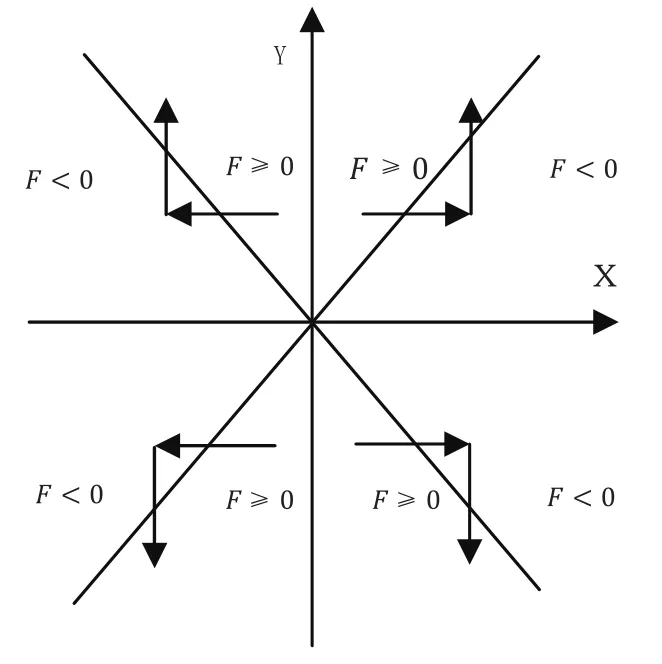
图2 逐点比较法运动判断图
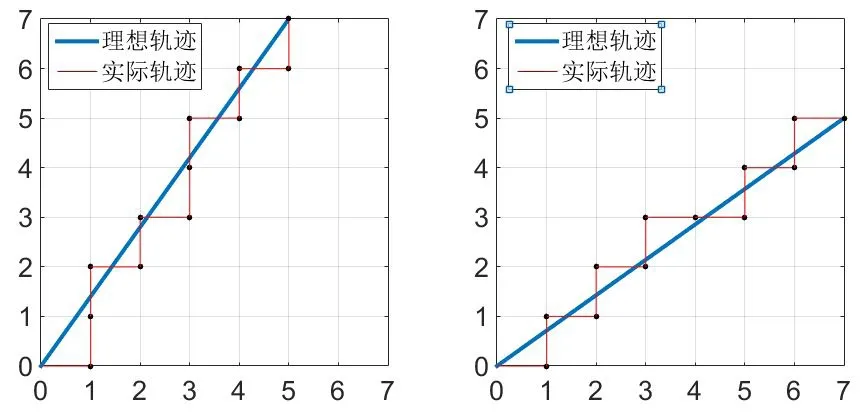
图3 逐点比较法运动效果
2.2 最小偏差法
最小偏差法和逐点比较法的执行步骤、判断依据基本一致,有所不同的是最小偏差法引入了不止沿着x轴和y轴插补,还引入了45度角插补,共把一个平面区域分成了八个卦限[7],其各卦限进给方向和偏差关系如表2所示,在具体卦限的具体进给方向和偏差判断如图4所示,F为偏差,F≥0时,挤出机构沿Y=X或Y=-X运动,F<0时挤出机构沿着X或Y轴运动,步进电机M1和M2以相同的速度顺时针或逆时针同向转动时,就可以沿着X轴运动,步进电机M1和M2以相同的速度顺时针或逆时针反向转动时,就可以沿着Y轴运动,当步进电机M1转动,步进电机M2静止时,滑块将沿着Y=X方向移动;当步进电机M2转动,步进电机M1静止时,滑块将沿着Y=-X方向移动。
同样以0.1mm为步进电机的脉冲当量,假设当前点为C(0,0),目标点为D(0.4,0.7)或D(0.7,0.4),经过MATLAB仿真得到最小偏差法运动效果图5,图中的细线代表实际走过轨迹,粗线代表理想轨迹,由图5可知,最小偏差法比逐点比较法在效率和精度上有了明显的提高,但依然存在着较大的误差,效率也并不高,所以现在就引入改进算法。以上两种算法只局限于沿着X轴、Y轴和45度方向进给,其他角度的直线只能靠插补来实现。我们不妨假设,可以沿着其他角度插补,这就需要两个步进电机同时以不同的速度运动,这样就可以实现各种角度的高精度、高效率运动。

表2 最小偏差法插补公式表
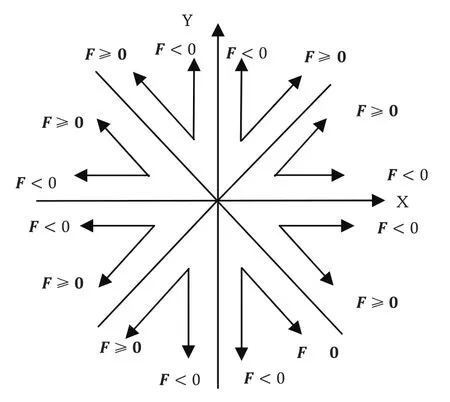
图4 最小偏差法运动判断
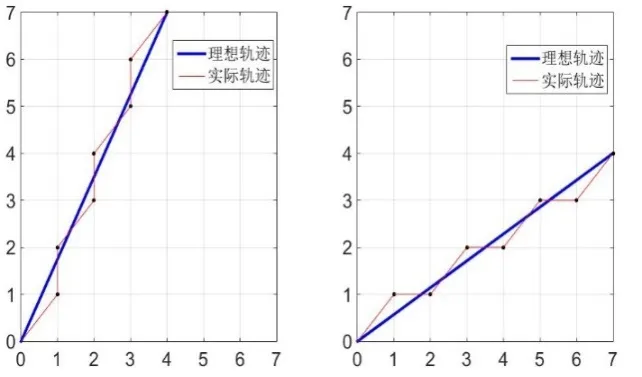
图5 最小偏差法运动效果图
2.3 改进算法
2.3.1 原理描述
为了实现机构X、Y轴的联动,需使电机M1和M2同时以不同速度运动,同时开始同时结束,其第一卦限运动示意图如6所示。

图6 改进算法运动示意图
由图6可知,对于任意方向的直线插补,ΔX和ΔY的大小并不一定相同,此时:
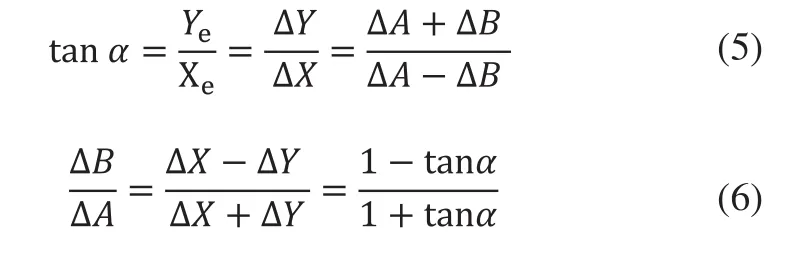
由此我们可以得到两个步进电机的转动的线位移的比例关系,两个电机需要在相同时间完成转动,所以电机的位移之比等于角速度之比,又由于步进电机的角速度ω1、ω2是由控制器输出的脉冲的周期T1、T2决定,所以可得:
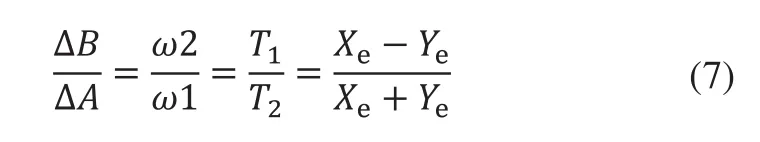
由式(7)可知我们可以通过控制其输出脉冲的周期以达到控制机构滑块沿着任意方向运动。
这种方法的难点在于周期大小选择,脉冲周期过大和过小都会无法驱动步进电机,所以我们可通过设置及极限值的方法来限制不合适的脉冲,步进电机可以平稳驱动的脉冲周期大约为10μ s~3ms,对于128细分的驱动器,最小的驱动周期可达3μs;对于普通的驱动器没有那么多细分,由式(7)可知,当直线方向接近Y=X时,驱动步进电机M2的脉冲周期则趋于无穷大,这样这种方法就会产生死区,为了解决这一缺陷我们可以采取和最小偏差法相结合的方法,在死区时采用最小偏差法,其他时候采用这种方法,这样就会大大提高机构的运动速度和精度。
2.3.2 算法实现步骤
对于算法的实现,需要确定CoreXY机构两个步进电机的旋转方向、驱动脉冲周期以及脉冲数目,因此可以分为以下3个步骤:

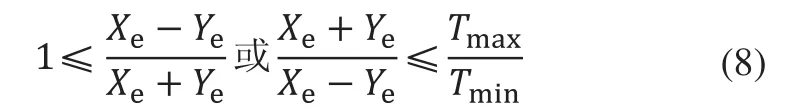
若符合要求,则适用改进算法;若不符合,则适用最小偏差法。
2)电机方向和步数确定:步进电机的转动方向和转动步数可以由下式确定:
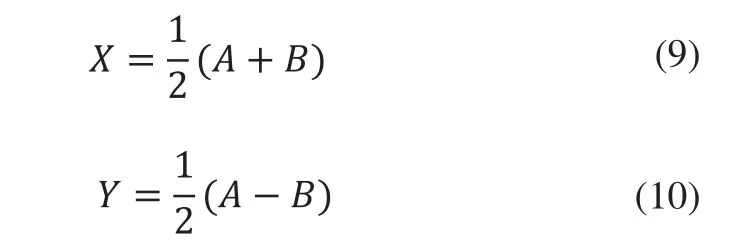
式中X、Y为挤出机构沿X轴和Y轴脉冲当量的数目,可以通过Xe,Ye分别除以脉冲当量得到,A、B分大小别为步进电机M1和M2所需转动的脉冲数,符号代表步进电机的转动方向。
3)电机脉冲周期确定:由式(7)可以确定步进两个步进电机脉冲周期之比,通常以周期较小者为基准周期,基准周期选用可平稳驱动步进电机的最小周期Tmin。
假设取当前点为C(11.3,-8.4),目标点为D(12.5,-8.7),脉冲当量为0.01mm,规定最小周期Tmin=0.5ms,最大周期Tmax=2.5ms,则易得Xe=1.2,Ye=-0.3,换算为脉冲当量数目为X=120,Y=-30,方向为第四象限。
(1)由式(8)知Xe,Ye在不等式范围内,适用改进算法。
(2)由式(9)、式(10)计算得A=90,B=150,步进电机M1的需要转动的脉冲数为90,方向为逆时针,步进电机M2的需要转动的脉冲数为150,方向为逆时针。
3 结束语
我们分析了CoreXY机构的运动特性以及基于该机构3D打印机的常用运动控制算法,对比的各种算法的优缺点,提出了一种改进算法,运用这种算法,配合数据校正算法,再配合步进电机的梯形加减速算法[8],PID算法控制挤出丝的温度,配合Z轴和E轴的运动,可以获得很好的打印精度和速度。

