多无人机对组网雷达系统的协同干扰*
张 哲,吴 剑
(南昌航空大学, 南昌 330063)
0 引言
在现代电子对抗中,组网雷达系统具有较强的抗干扰能力,其军事作战应用广泛。欺骗干扰是一种常用的干扰方式,如何对组网雷达实施行之有效的干扰,是当今电子对抗界面临的一个重大问题[1]。
文献[2]提出了一种基于最小识别概率的虚假航迹优化方法,文献[3]研究了飞行器协同控制问题,利用了最优控制算法对航迹进行了仿真,有一定的可行性。文献[4-10]对假目标和飞行器间运动模型的参数进行了优化,但协同干扰方面并未详细研究。文献[11]重点分析了组网雷达系统的发展现状以及相关技术,提出了实现干扰所需要解决的问题。文献[12]利用多变量间的耦合关系和勒让德伪谱法对单机欺骗单部雷达的模型求解,由于耦合变量间关系复杂,运动参数较多使得模型求解存在较大误差,在实际应用中较难实现。
文中在进行合理的假设分析后,提出了一种多无人机对组网雷达协同干扰的技术,利用无人机、雷达与假目标三者位置的几何关系,建立了多机协同飞行的运动模型。给定任意一条虚假航迹,结合PSO算法求解得到综合考虑无人机数量、航迹坐标以及运动参数的最佳方案,完成航迹欺骗的同时也满足了飞行速度约束,具有一定参考价值。
1 多机协同干扰的航迹优化模型
1.1 航迹欺骗原理
在多无人机协同飞行的过程中,无人机搭载的干扰设备对接收到的雷达信号处理后转发回对应雷达,组网雷达信息融合中心将干扰信号形成航迹点信息,基于一定的融合规则,得到多部雷达在统一坐标系下同一空间位置的多个目标航迹点,最终形成了目标的虚假航迹如图1。通过协同控制无人机的飞行航迹,可在敌方的组网雷达系统中形成一条或多条欺骗干扰航迹,迫使敌方加强空情处置,达到欺骗的目的。

图1 多机协同干扰组网雷达示意图
1.2 数学模型
1.2.1 模型准备
多架无人机对组网雷达系统的干扰问题,可先讨论单架无人机对雷达的干扰。由于组网内每部雷达的监测距离受限,即通常判断在某个时刻,若虚假目标信号能够同时被3部或3部以上的雷达监测,雷达组网系统则认为其为真实目标。通过不同时刻,检测到连续的合理目标点,构成一条虚假航迹。在定高飞行模式下,由电磁波传播特性,无人机、假目标和雷达三者相对位置在一条直线上,如图2所示。
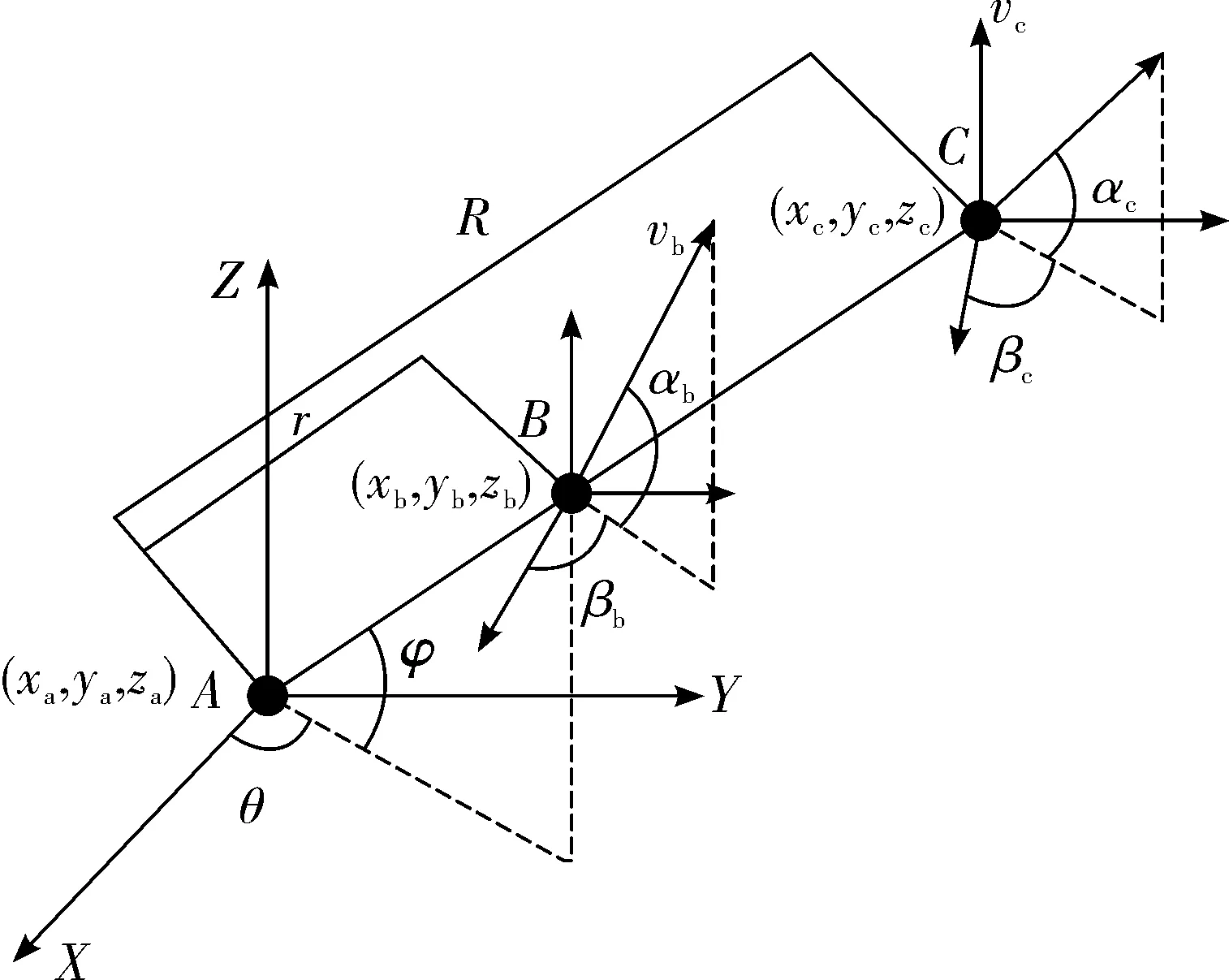
图2 雷达、无人机和假目标位置关系
在无人机飞行过程中,必然会受到外界环境和自身内部因素的影响。为了完成协同干扰,在建模之前做如下假设:1)无人机在空间区域做直线运动,给定初始航向、航速和飞行高度;2)无人机飞行时视为一个质点,不会受到天气、导弹攻击等因素的干扰且不考虑转弯、爬升和俯冲等;3)不考虑无人机产生的真实目标回波,每隔一定时间获取一批目标的空间状态数据。
1.2.2 单架无人机与假目标的运动模型
由图2知,在空间区域中,A表示雷达,B表示无人机,C表示假目标。假设假目标位置坐标为(xc,yc,zc),无人机坐标为(xb,yb,zb),雷达坐标为(xa,ya,za),s表示时刻,β为初始航向角,v为无人机飞行速度,r为两者之间的径向距离,θ为俯仰角,φ为方位角。由于高度h恒定,因此给出二维平面内雷达、无人机和假目标的位置关系表达式,通过几何关系,在直角坐标系下建立单架无人机与假目标的运动模型为:
(1)
(2)
(3)
由于模型假设飞行高度h恒定,即α=0,得到定高飞行下无人机与假目标的运动模型为:
(4)
为了更直观的反应雷达、无人机与假目标三者之间的运动关系,现将直角坐标系下的位置关系转化为以雷达位置坐标为原点的球面坐标系下的方程为:
xs=Rs·cosθ·cosφ
ys=Rs·cosθ·sinφ
zs=Rs·sinθ
(5)
进而对(5)式求导,得到:
(6)
将式(4)代入式(6),改写成矩阵形式,可得单架无人机与假目标在以雷达坐标为原点的球面坐标系下的运动方程:
(7)
联立式(4)、式(6)、式(7),得到:
(8)
将式(5)代入式(8),化简后解得运动参数:
1.2.3 多无人机协同干扰的运动模型
基于单架无人机与假目标运动模型,进一步研究多无人机协同飞行下的运动。
将n个雷达坐标与S时刻的虚假坐标相连,在平面内会产生n·S条直线,确定平面z=h与n·S的交点,即无人机可能出现的位置坐标。在研究多机协同运动时,每架无人机在平面上的位置如图3。

图3 xoy面无人机位置的时刻坐标
由于无人机做直线运动,将速度vs分解为水平方向vx和竖直方向vy,即
(10)
现每隔△t时间间隔从空间中获取一批目标的空间状态数据,对应的第2个时刻的无人机的位置坐标为:
(11)
在第3个时刻,无人机的位置坐标为:
(12)
同理,根据上述方法,可以计算得到在第S时刻,无人机的位置坐标为:
(13)
当多架无人机在一个拥有n部雷达的组网雷达系统干扰下飞行时,在以每部雷达坐标为原点的球面坐标系下,结合无人机与假目标的运动方程,在虚假航迹给定时,便可分别求得任一时刻无人机和假目标的位置坐标,进而能够更准确地分析无人机的运动状态,研究多机协同飞行干扰策略。
2 模型求解
2.1 约束条件
无人机与假目标在运动过程中,其速度应受到一定约束:vmin≤vs≤vmax,这里取vmin=120 km/h,vmax=180 km/h。由于是定高飞行模式,高度一般在2 000~2 500 m,这里取h=2 300 m。
2.2 粒子群算法
粒子群算法(PSO)是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中获得最优解。组网雷达系统每隔△t时间间隔从空间罗列出平面n·S的交点,即无人机可能出现的位置坐标如图4所示。根据上节所建立的运动模型求解出任意时刻无人机的运动状态,由速度约束条件,算出点与点之间可能的路线,即无人机可行路线。

图4 空中无人机的运动
2.3 求解步骤
假设i表示假目标的初始位置,j表示假目标经过路径中任意一点位置,设n部雷达同时作用假目标,由于假目标、无人机和雷达三者在同一直线,即雷达与假目标间有n条线段,无人机飞行高度h已定,与这些线段将产生n2个交点,若假目标可飞向另外的(S-1)个目标点,则产生n2·(S-1)条可行路径。同理,用Mij表示可行线,则S个目标点一共可以产生n2·S·(S-1)/2条可行线。具体求解步骤如下:
step1输入组网雷达系统中n部雷达的坐标(xam,yam,zam),其中m=1,2, ...,n。固定无人机飞行高度h。
step2求得z=h所在平面与假目标、n部雷达连线的交点,即无人机可能的飞行区域。
step3由模型中无人机速度的约束,即vmin≤vs≤vmax,根据r=v·△t判断两点之间是否为可行线。
step4若两点之间为可行线,则Mij+1,挑选并记录下该条飞行路线;否则剔除该条路线,保持Mij不变,重复step3。判断下一目标点。
step5遍历S个时刻内所有的目标点,生成所有的可飞行路线,并进行分配路线,由运动模型以及坐标公式求解位置坐标。
3 仿真分析
已知组网雷达系统中共有5部雷达,位置坐标分别为雷达1 (80,0,0),雷达2 (30,60,0),雷达3 (55,110,0),雷达4 (105,110,0),雷达5 (130,60,0),单位为km。组网雷达监测区域如图5。无人机飞行高度为2 300 m,利用首点迭代法[13]产生一条虚假航迹如图6。取△t为10 s,S=20 s,即飞行时间为200 s,假目标初始位置坐标为(60 600,69 982,7 995),单位:m。

图5 组网雷达扫描区域
根据无人机与假目标的运动模型,基于PSO算法结合上述求解步骤可算出多无人机对组网雷达协同干扰下的航迹生成如图7,进而解得至少需要17架无人机协同飞行才能实现所产生的虚假航迹,分别对17架无人机编号,限于篇幅有限,只给出了每架无人机起点和终点的位置坐标如表1。由式(4)、式(5)以及每架无人机的位置坐标,解出无人机与假目标的速度如图8和图9。

图7 无人机航迹生成图


图8 无人机飞行速度

表1 每架无人机的位置坐标

图9 假目标的运动速度
4 结束语
多无人机对组网雷达系统的协同干扰是一种十分有效的航迹欺骗方法。文中针对前人研究中的模型参数求解过程复杂,协同飞行效果不佳和不满足约束条件等问题,建立一种多无人机协同干扰的航迹优化模型,结合PSO算法求解得到综合考虑无人机数量、航迹坐标以及运动参数下的最佳协同方案,满足速度约束的同时优化了航迹,对实际应用具有参考价值。

