某型制导火箭子母弹弹道仿真与性能评估方法*

王海峰,王广伟,贾 波,邵庆新

(63850部队, 吉林白城 137000)

0 引言

某型制导火箭子母弹研制总要求中明确指出在不高于4 500 m的海拔高度上,最大射程不小于某一距离。回答这类指标要求的通常做法,是在极限边界条件下进行飞行试验,依据飞行试验数据给出评定结果。对于该型弹药至少需要分别在海拔0 m和4 500 m高度的阵地上进行不小于射程指标的射击试验。由于射程远,试验安全风险大,平原地区人员稠密,极限边界条件下试验场地选取难度非常大。为降低安全风险,试验场地只能选择在人烟稀少的西部,但西部地区普遍较高,处于海拔1 500 m以上,不能满足海拔0 m的试验条件。文中在全面掌握飞行机理,摸清弹道特性的基础上,采用理论计算与射击试验结合的模式,将其它海拔高度弹道性能试验数据与海拔0 m高度弹道性能联系起来,实现极限边界条件下的准确弹道仿真,科学、全面、客观、高效考核弹道性能。

1 弹道仿真模型

1.1 制导控制策略

某典型制导火箭弹制导舱采用全程三通道制导控制策略。滚转通道采用全程滚转稳定控制方案,如图1所示。

航向通道采用全程速度矢量控制方案,如图2所示，使火箭弹速度矢量在地面坐标系X-Z平面的投影始终对准目标。

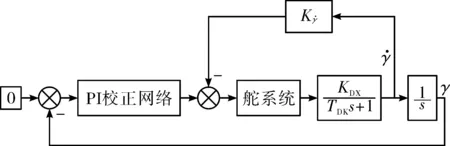
图1 滚转控制通道结构框图

俯仰通道以无控弹道为基准弹道分为两个阶段进行控制。

1)火箭弹出炮管后, 俯仰控制通道根据基准弹道给出的弹道倾角进行速度矢量控制,控制方案与航向通道相同;

2)火箭弹飞行到降弧段一定高度,俯仰控制通道引入带落角约束的比例导引控制,内回路为过载自动驾驶仪，如图3、图4所示。

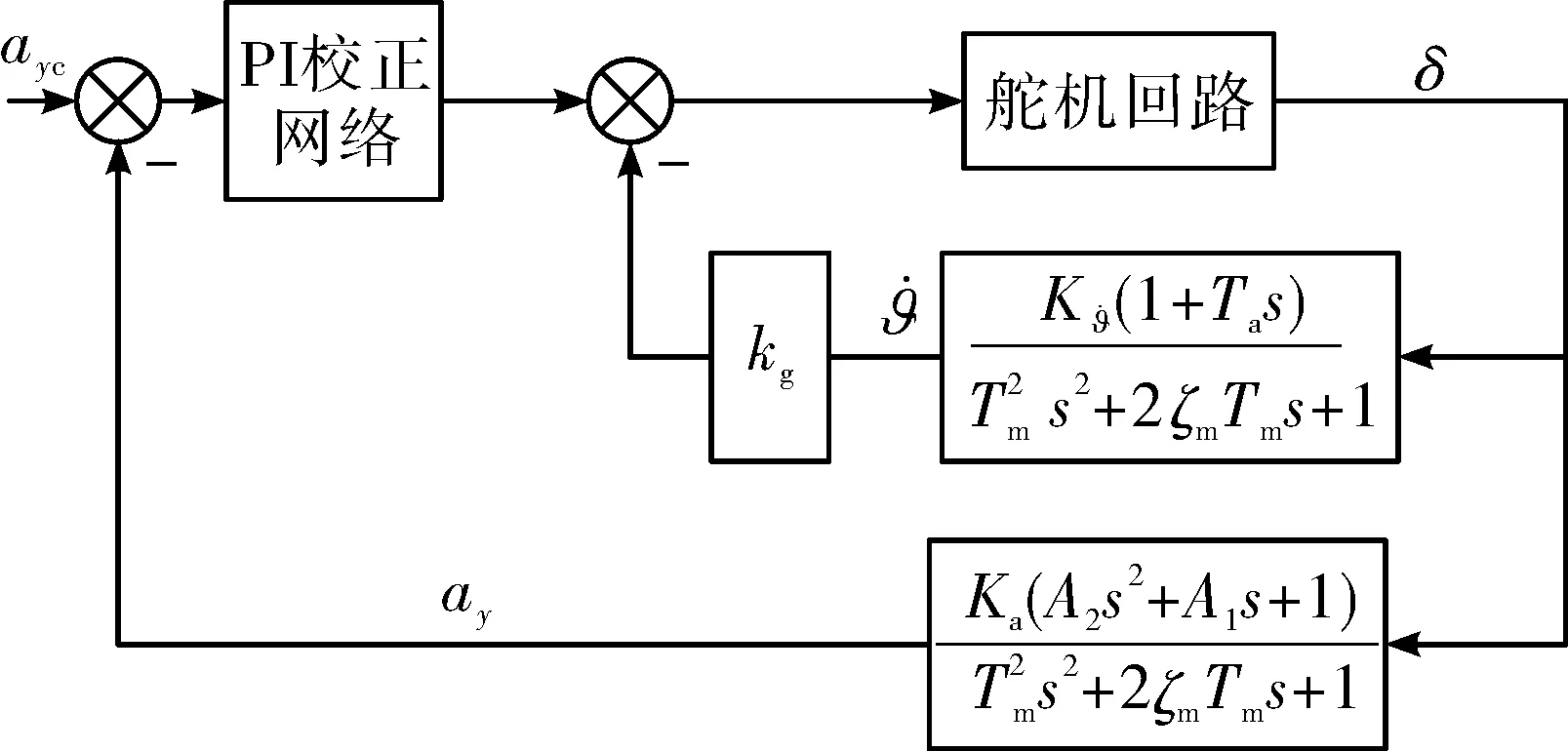
图4 俯仰通道过载自动驾驶仪结构框图

1.2 弹道模型

制导火箭子母弹飞行可分为滑轨段、母弹自由飞段、子弹飞行段。滑轨段包括静止期、约束期、半约束期的受力运动模型,此段箭体飞行需要考虑飞行中质量变化、发动机推力作用、重力及重力矩、滑轨槽阻力及导转力矩;母弹自由飞段包括火箭发动机工作时期的主动段和发动机关机后的被动段,这段飞行中控制系统工作,运动模型中不仅考虑飞行中质量变化、发动机推力作用、重力、科氏力、气动力及力矩,还要考虑控制系统产生的控制力及力矩;子弹飞行段是指子母弹战斗部从开舱到子弹着地的飞行过程,子弹外形近似为圆柱体,飞行阻力较大,开舱高度低,子弹段飞行距离较短,子弹飞行可近似为质点运动,只考虑重力和科氏力。

为提高模型的适用范围与精度,在正球体地球、地形及中心重力场假设下,建立弹箭弹道模型[1]。利用发射动力学、刚体动力学建立母弹刚体运动模型;不考虑子弹姿态变化对飞行阻力的影响,将子弹运动近似为质点运动,建立子弹质点运动模型,采用虚拟弹道方法,计算子弹弹着散布中心。

2 关键弹道特性参数的确定

弹道仿真模型涉及参数包括武器系统与箭体所固有的特性参数和地理气象环境参数,武器系统与箭体所固有的特性参数包括发射滑轨结构参数、弹体结构参数、发动机特性参数、控制系统参数、气动参数以及起始扰动参数。这些参数受环境条件影响较小,在不同的地理气象环境条件下获取到的这些参数基本上是一致的。因此,只要在某给定环境条件下获得武器系统与箭体所固有的特性参数后,就可以仿真不同地理气象环境参数下的弹道特性。武器系统与箭体所固有的特性参数的准确性很大程度上影响着仿真精度,这些参数可以通过地面试验和飞行试验手段获取。

2.1 通过地面试验获取的参数

通常情况下,可以通过静态测量方式获取发射滑轨结构参数、弹体结构参数;通过发动机推力台试验,获取常、高、低温条件下推力曲线与比冲;利用数值流场模拟与风洞试验,获取舵机不同偏转下的气动参数;利用地面半实物仿真验证控制系统模型参数的正确性。

2.2 通过飞行试验获取的参数

气动参数中阻力系数影响弹箭飞行最为显著,因此,起始扰动及阻力系数的准确性很大程度上决定了弹道仿真的精度。在弹道仿真及性能评估中,起始扰动及阻力系数准确获取成为弹道参数获取工作的重点。利用飞行试验数据,结合无控、有控弹道模型,采用离轨点速度、姿态参数求差方法确定下沉角,采用主动段终点弹道倾偏角符合的方法确定弹轴起始摆动速度,采用参数辨识方法从速度数据中辨识无控火箭零阻系数。

零阻系数辨识常用的是分段常值Chapman-Kirk算法[2](参数微分修正法)。这种算法的当前段辨识结果影响后续段辨识精度,局部误差会不断累积放大,辨识结果通常呈喇叭口形状离散,当速度测试误差大或需要辨识的马赫数范围宽时,甚至会出现辨识不收敛。

以经典参数微分修正算法为基础,结合样条拟合技术建立弹道参数整体辨识方法,扩展参数辨识范围,提高参数辨识精度。弹道参数整体辨识方法从待估参数、原始信息残差的全局最优出发,克服了分段常值算法的不足,有效地利用了全弹道速度信息,高精度地辨识出阻力特性参数。

自变量为飞行马赫数Ma,待辨识参数为无控火箭零阻系数Cx0(Ma),Cx0(Ma)可用(N+1)段的L阶样条函数表示为:

(1)

Bj(x)为L次B样条函数[3]第j项,αj为第j项系数,辨识Cx0(Ma)实质就是如何确定系数αj。Bj(x)定义为:在Ma∈[Mamin,Mamax]区间内选取N个内节点,将区间分成(N+1)份,分别以第1份、第(N+1)份的长度在区间两端各延伸L段,则共有(2(L+1)+N)个节点Mai,i=1,2,…,(L+1)+N,则

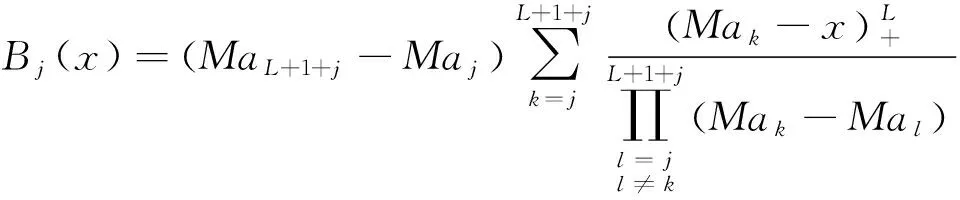
j=1,L+N+1

(2)

(3)

将Nt个速度实测值与计算值的残差平方和作为目标函数:

(4)

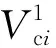
(5)

若使SSR最小,则

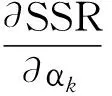
(6)

k=1,2,…,N+L+1

(7)

解微分修正方程(7)可求解出每次迭代修正量Δαj。

在地面坐标系中计算弹道直接得到的是3个坐标轴方向上的速度分量VX、VY、VZ,转换为和速度的公式为:

(8)

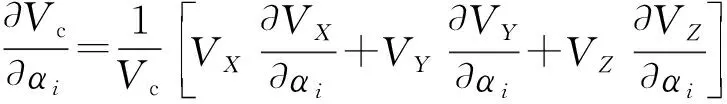
i=1,2,…,N+L+1

(9)

3 仿真计算与性能评定

3.1 某型弹道特性参数确定

通过地面静测、试验与流场模拟,确定该型制导火箭子母弹发射滑轨结构参数、弹体结构参数、发动机特性参数、控制系统参数、气动参数;利用不同试验阵地高度、不同药温条件下所做的命中精度、可靠性评估等飞行试验科目的速度、姿态、坐标、舵机偏转及气象数据,采用上述的弹道参数精确化方法,确定的下沉角为-1.4°,纵向初始摆动角速度为-0.15 rad/s。采用弹道参数整体辨识方法辨识零阻系数结果与数值模拟对比如图5示。

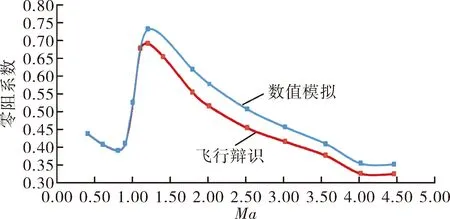
图5 无控零阻系数辨识结果与数值模拟结果对比

3.2 弹道性能评定的标准条件

1)地球、地形条件

a)地球为正球体,球径取6 371 110 m;

b)重力加速度g=9.80 m/s2,指向地心;

c)弹着点与炮口同高;

d)火箭炮俯仰轴水平,身管轴线与俯仰轴相垂直;

e)科氏加速度为零。

2)弹道条件

a)弹箭质量为表定值,且呈轴对称分布;

b)药温为15 ℃;

c)尾翼及舵机展开后,弹形符合定型图纸规定;

d)推力沿弹轴方向,发动机工作时间、装药质量、推力大小与设计吻合;

e)控制系统工作正常,方案弹道的确定原则与产品设计说明书一致。

3)气象条件

a)地面(海拔高0 m)标准气温为15 ℃,绝对湿度为846 Pa(相对湿度为50%),地面标准虚温为15.9℃(288.9 K),虚温随高度变化31 000 m下服从炮兵标准气象条件[4],31 000 m以上服从国际标准气象条件[5];

b)地面标准气压p0为1 000 hPa,气压随高度变化服从大气铅垂平衡条件:

c)在弹道所有高度风速为零。

3.3 子母弹射程指标评定

以某典型远程火箭子母弹为例,进行弹道性能评估,假定其射程指标为180 km。在海拔0 m高度,设定目标点在地面坐标系中坐标:X=180 000 m、Z=0 m、Y=-2 543 m(对应海拔高度0 m),对应的预定开舱坐标:X=179 340 m、Z=0 m、Y=-1 874 m(对应海拔高度650 m)。按型号设计的射击初始诸元解算方案,制导子母弹无控弹道射程小于理论射程,导引段通过滑翔增程达到实际射程并实现减速目的。采用无控弹道解算初始射击诸元和装订的方案弹道倾角,解算出的射角为52.336 7°。

利用上述建立的模型、获取的弹道参数在标准条件下进行弹道仿真,仿真计算得到的开舱坐标X=179 340 m、Z=0 m、Y=-1 874 m,开舱时刻弹道倾角为45.14°,开舱时刻飞行速度为560 m/s,弹着坐标Xc=180 004 m、Zc=0 m、Yc=-2 543 m,装订的方案弹道倾角与实际弹道倾角如图6,飞行速度变化如图7,舵机1、舵机2偏转如图8,舵机3、舵机4偏转如图9。

图6 子母弹方案弹道倾角与实际弹道倾角对比

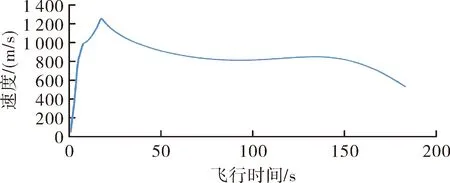
图7 子母弹飞行速度变化

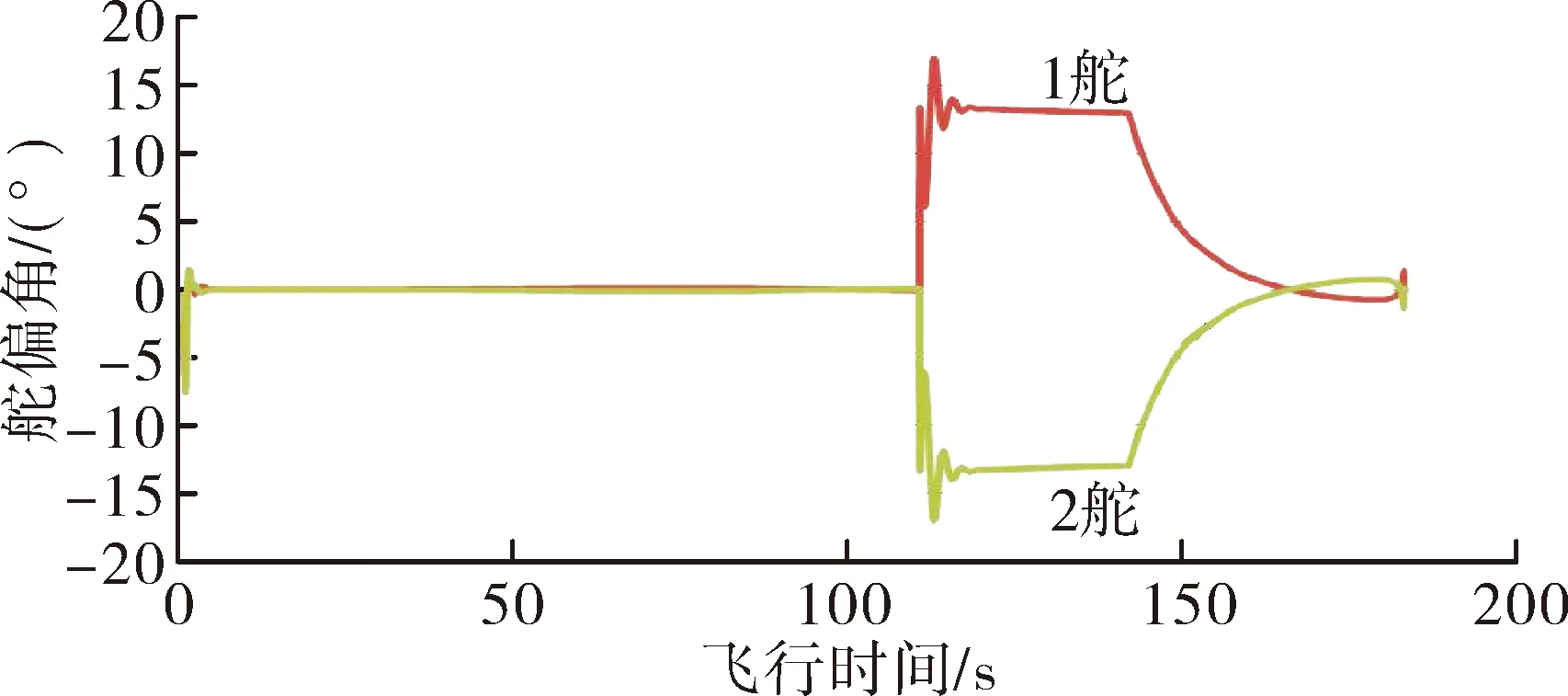
图8 子母弹舵机1、舵机2偏转变化

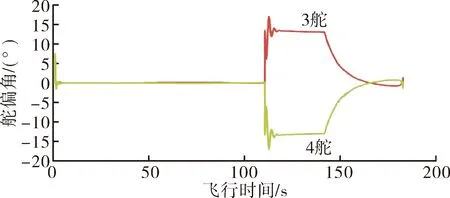
图9 子母弹舵机3、舵机4偏转变化

从标准条件下仿真结果可以看出,0 m海拔发射阵地,子母弹能够在预定位置开舱,命中180 km目标,且在比例导引前,舵偏较小,控制系统仍有较大修正余地,具备较好抵抗干扰的条件。因此该型弹药在0 m海拔发射阵地满足最大射程180 km的指标要求。

4 结论

文中建立制导火箭子母弹理论弹道模型,给出了关键参数的辨识方法,形成完整、科学、可行的制导火箭子母弹弹道仿真与性能评估技术,利用非边界极限条件下飞行试验数据完成了边界极限条件下的射程指标评定,为全面客观评估其弹道性能提供依据。