拉普拉斯变换在广义积分及微分方程求解中的应用

董姗姗，宫原野

（1.安徽科技学院 信息与网络工程学院，安徽 凤阳 233100；2.蚌埠学院 计算机工程学院，安徽 蚌埠 233000）

0 引言

拉普拉斯变换作为积分变换的重要内容，在通信类、控制类、电气类等专业课中有着广泛的运用［1-3］。如控制工程中研究阻尼振动需要用到狄利克雷积分，工程热物理中研究热传导需要用到泊松积分，理论光学中研究光的衍射需要用到菲涅尔积分等。高等数学运用传统的积分方法求解这类积分显得非常复杂，在运算中还需要特殊的运算技巧［4-6］。物理学与工程（电路、线性复杂网络等）方面的许多问题都可以归结为微分方程的定解来考虑［7-11］，通过拉普拉斯变换可以很方便地对微分方程进行求解。本文通过大量的例子，重点讨论拉普拉斯变换在广义积分与微分方程中的应用。

1 预备知识

定义［2-3］设函数f(t)在区间(0,+∞)上有定义，且积分在 Res ＞c时收敛，由此积分结果记为F(s)，称为函数f(t)的拉普拉斯变换，记为F(s)=L{f(t)}，即

式中，F(s)称为f(t)的象函数，f(t)称为F(s)的原函数。

根据式（1）可以得到如下结论：若象函数F(s)的所有奇点都位于y轴左侧，则

性质1设L{f(t)}=F(s)，若函数f(t)可导，则

性质2设L{f(t)}=F(s)，若函数f(t)可积，则

性质3设L{f(t)}=F(s)，若象函数F(s)可导，则

性质4设L{f(t)}=F(s)，若象函数F(s)可积，则

性质5设L{f(t)}=F(s)，则

2 利用拉普拉斯变换求解广义积分

例1计算。

解上述积分为傅汝兰尼积分的一个推广，利用拉普拉斯变换求解。

根据式（6）可知

再根据式（2）可知

例2计算狄利克雷积分。

解法一由于狄利克雷积分收敛，引入参变量t，使其成为t的函数。令，设L[f(t)]=F(s)，则有

再取F(s)的拉普拉斯反变换，则。

解法二根据根据其积分性质可知

再根据式（2）可得

解法三根据式（6）可知

例3计算。

解上述积分为狄利克雷积分的推广，由，根据式（7）可得

根据象函数积分性质可知

根据式（2）可知

例4计算。

解由积分，根据式（4）可知

例5计算欧拉-泊松积分。

解根据达朗贝尔判别法可知欧拉-泊松积分收敛，引入参变量t，使其成为t的函数。

根据F(s)的反变换，由可以推导出进而得出。

3 采用拉普拉斯变换求解微分方程

利用拉普拉斯变换求解微分方程的解题思路：

1）微分方程两端同时取拉普拉斯变换，将常系数的微分方程转化为象函数的代数方程；

2）求解象函数满足的微分方程，得到象函数；

3）对象函数进行拉普拉斯反变换，从而得到原方程的解。

例6求常微分方程y″(t)-3y′(t)+2y(t)=2e3t，满足初值条件y(0)=2 ，y′(0)=3 的解。

解设L{y(t)}=Y(s)，在方程两端取拉普拉斯变换可得

将初值条件代入，得到关于Y(s)的代数方程为

利用待定系数法将式（8）分解为3 个简单分式和的形式，即

再利用拉普拉斯变换的逆变换，可以得到满足初始条件方程的解为

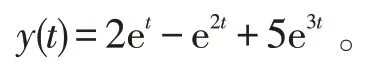
例7求解分段微分方程

其中y(0)=0，y′(0)=0。

解方程两边同时进行拉普拉斯变换得

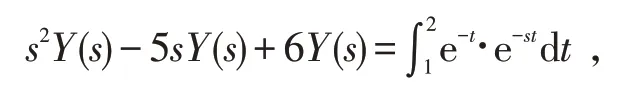
整理得

对式（9）求拉普拉斯反变换可以得到

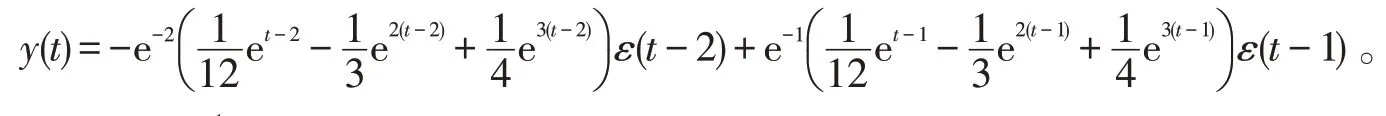
例8求微分方程组的解。

解在方程两边同时进行拉普拉斯变换得

取X(s),Y(s)拉普拉斯反变换可得。

4 结语

狄利克雷积分、欧拉-泊松积分等工程领域常用的广义积分计算有多重方法，本文通过引入参变量t构造新的函数，进而运用拉普拉斯变换的相关性质对这类积分的计算给出了详细的分析思路及计算方法。本文所提出的方法较为简单，可以在求解这类广义积分中进行推广。在微分方程求解过程中，巧妙地运用拉普拉斯变换，可以在一定程度上简化运算，丰富了微分方程求解的方法。