基于Workbench的液压联轴器振动研究

胡 斌,贾会星,何 凯

(滁州职业技术学院 汽车工程系，安徽 滁州 239000)

船舶、轧机以及大型化工机械等重型机械机器设备通常使用液压联轴器进行传动。液压联轴器通过控制注入油的压力，能较大幅度地调整传递的扭矩值[1]。由于液压联轴器在传动过程中靠着内轴和外套的接触碰撞传递扭矩[2]，在传递较大扭矩情况下液压联轴器会出现振动，甚至可能会发生共振的现象。目前国内很多学者只针对液压联轴器的应力分析或者抗冲击方面进行研究，并没有针对液压联轴器在高速环境下出现的振动问题进行研究。

本文对满足静力学条件下的液压联轴器进行振动分析。首先利用UG对液压联轴器进行三维建模，如图1；将三维建模导入有限元软件Workbench后进行模态分析，得到固有频率和振型图[3-4]；从中找出变形量最大的两处位置分别位于液压联轴器的内轴和外套，对内轴和外套进行有预应力的谐响应分析，得到相应的响应关系、结构的危险频率及动态特性。

图1 液压联轴器三维图Fig.1 Three-dimensional drawing of hydraulic coupling

1 模态分析

通常液压联轴器是通过联接内套与传动轴之间过盈配合来传递扭矩的，因此，本文选取应力分布更均衡的实心轴液压联轴器，将其三维模型导入Workbench后进行模态分析，得出其自身转速对振动的影响。

1.1 前处理

已知液压联轴器内轴材料为42CrMo、外套材料为40Cr，有限元前处理包括单元类型定义、材料属性选取、网格划分。经过Workbench网格处理，外套被划分为27 298个节点、5 400个单元，内轴被划分为个25 815节点、5 268个单元，划分网格后的联轴器几何模型如2所示。

图2 网格模型Fig.2 Grid model

模态分析理论公式如下[5]：

(1)

由公式1结构无阻尼自由振动方程可知在理论求解模态分析中没有力，则液压联轴器在Workbench软件中的加载方式如图3所示，即A端和B端分别约束X、Y、Z方向的转动和移动。

图3 模态约束模型Fig.3 Modal constraint model

1.2 模态分析结果

在Workbench中完成材料定义、网格划分、工况加载后，进行模态求解。模态算法有7种，对于该模型采用分块法可使其求解收敛速度更快。分块法求解该模型后得到各阶振型图，如图4所示。分块法同样可以用来求解特征值对称的大矩阵问题。

图4 模态分析振型图Fig.4 Mode diagram of modal analysis

根据模态分析结果绘制表1。

表1模态分析结果
Table1Modal analysis results

振型阶次固有频率/Hz振型描述最大变形量/mm1 2 155.0沿Z轴方向2.7922 155.1沿Y轴方向2.3832 966.2沿Z轴方向2.6243 818.8沿X轴方向2.6454 253.2沿X轴方向2.5064 253.5沿X轴方向2.64

2 谐响应分析

液压联轴器在通过内轴、外套的碰撞接触传递扭矩过程中很容易出现共振、疲劳以及其他受迫振动引起的有害效果。谐响应分析通常采用4种方法即完全法、缩减法、模态叠加法和时程分析法[6]计算模型在稳态情况下的受迫振动，而不考虑瞬态振动。由表1模态分析的前6阶结果可知：1、2两阶固有频率相差0.1 Hz，2、3阶固有频率相差811.1 Hz，3、4阶固有频率相差852.6 Hz，4、5阶固有频率相差434.4 Hz，5、6阶固有频率相差0.3 Hz。由于两阶固有频率相差越小，越容易出现破坏现象[7]，因此对液压联轴器的谐响应分析主要集中在1、2和5、6阶固有频率之间。

2.1 内轴的谐响应分析

由Workbench软件单独显示的内轴模态振型图可以看出1到5阶振型变化中内轴固有频率和振型最大，由表1可知液压联轴器固有频率范围在2 155～4 253.5 Hz，在谐响应分析中给定激振频率范围为2 000～4 500 Hz和20步的载荷步数，选取内轴的外表面作为响应面运用模态叠加法进行谐响应分析，得到内轴的应力—频率曲线、应变—频率曲线分别如图5、图6所示。

图5 内轴应力—频率曲线图Fig.5 Stress-frequency curve of the inner shaft

图6 内轴应变—频率曲线图Fig.6 Shows the strain-frequency curve of the inner shaft

从图5可以看出：内轴应力在X、Y、Z三个方向上的分量均在第1阶处于峰值，之后随着频率的增加而下降；三个分量在3 500～4 000 Hz时出现了小幅度的突变，但始终没有超过第1阶的峰值。因此，液压联轴器的内轴应力主要考虑低阶频率的影响。

图6中的应变在X、Y、Z三个方向上也出现了第1阶峰值，之后开始下降。但X方向上的应变在3 200～3 600 Hz、3 600～4 000 Hz之间出现了2次突变，且都大于初始时候的应变值；而Z方向的应变虽然也发生突变但是并没有超过初始的值。因此，液压联轴器的内轴应变在X方向上不仅要考虑低阶频率，也要考虑3 200～3 600 Hz和3 600～4 000 Hz高阶频率的影响；在Y、Z方向上的应变还是考虑低阶频率的影响。

液压联轴器内轴的谐响应分析表明低阶频率比高阶频率对系统振动变形的影响更大，但是对于X方向上的应变，不仅要考虑低阶频率，也要考虑高阶频率的影响。

2.2 外套的谐响应分析

由Workbench软件单独显示的液压联轴器外套的模态振型图可以看出，第5阶振型图中外套在高阶固有频率下出现最大变形，从而可能出现共振现象。现以外套为研究对象，按照内轴谐响应分析的设置方法，即激振频率为2 000～4 500 Hz、载荷步为20步，选取液压联轴器外套的外表面为响应面进行外套的谐响应分析，得到外套的应力—频率曲线、应变—频率曲线分别如图7、图8所示。

由图7、图8可知，与内轴相似，外套在初始激振2 000 Hz时曲线从峰值开始下降，中间出现一些小的波动但是都没有超过峰值；当激振到达4 500 Hz时，曲线出现了比2 000 Hz高的峰值。因此，对于液压联轴器的外套来说，高阶频率是主要影响要素，虽然图7中X方向外套应力在4 500 Hz时没有到达峰值，但是也有向上的趋势。

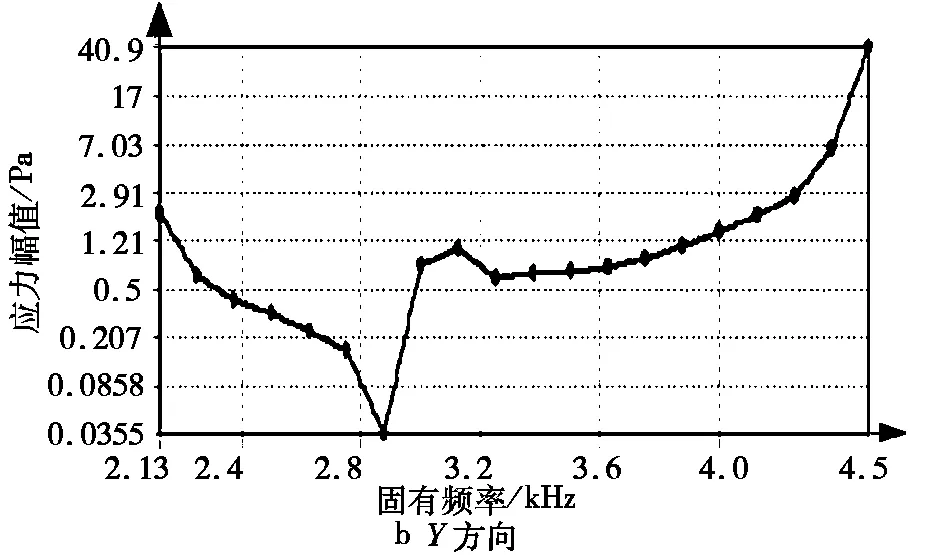
图7 外套应力—频率曲线图Fig.7 Stress-frequency graph of the jacket

图8 外套应变—频率曲线图Fig.8 Strain-frequency curve of the jacket

3 结论

通过对液压联轴器的模态与谐响应分析，可以得出如下结论：

(1)液压联轴器的内套主要受低阶频率影响，外套主要受高阶频率影响，因此液压联轴器的内套要尽力避开第1、2阶的低频，外套要避开第5、6阶的高频；但是对于内套来说，其X方向上的应变要同时避开低频和高频。

(2)液压联轴器的模态和谐响应分析，表明了液压联轴器的动态特性，可以以此为理论依据，以固有频率为设计变量，对液压联轴器的结构进行优化。但是谐响应分析是以稳态情况下的受迫振动为前提，对液压联轴器的瞬态振动并不适用。因此对液压联轴器瞬态振动的影响需要另外研究。