基于桩—土作用的滚石撞击双柱式桥墩动力响应分析

郭 森,孟园英,郭元凯,2,赵昌建，张桂通

(1． 长安大学公路学院，陕西西安710064;2． 贵州省质安交通工程监控检测中心有限责任公司，贵阳市 550000)

针对山区滚石撞击桥墩的问题，国内学者研究较少。国内学者展开对汽车、轮船撞击钢筋混凝土柱的研究较多，而考虑桩—土作用及上部结构约束下滚石撞击桥梁有限元精细化分析相关文献少有提及。

2002年刘建成等[1]运用LS-DYNA软件对一艘4万t级油轮与某斜拉桥桥墩的动态撞击作用进行了有限元仿真，得到了撞击过程中的船桥变形、桥梁的应力分布等随时间的变化时程曲线;曾靖[2]运用LS-DYNA仿真软件对山区预应力混凝土简支T梁进行了数值模拟，分析了不同因素工况下滚石撞击桥梁结构的动力响应;余志祥等[3]对落石冲击柱式桥墩进行仿真模拟，仿真考虑了不同落石直径、落石高度、落石速度、落石撞击角度等因素对撞击力的影响;连永庆[4]以山区某桥梁的桥墩结构为研究对象，对滚石撞击桥墩的撞击力、桥墩的应力分布和增设防撞措施后的桥墩动力响应分析进行研究，但未考虑桩—土的相互作用;Philipe Berther-Rambaud等[5]开展了数组落石冲击混凝土防护板实验，分析了混凝土防护板遭到落石冲击后的损伤破坏情况，并在此基础上提出了一种缓冲落石冲击的结构形式;Julien Lorentz等[6]展开落石撞击刚性墙的实验，并在试验的基础上得到了落石撞击力随着高度变化的关系曲线。

本文旨在基于考虑桩—土作用及上部结构约束作用复杂边界条件下，探讨不同结构形式桥墩(独柱墩、双柱墩)受滚石撞击时桥墩的动力响应：撞击力、关键部位节点位移、桥墩钢筋应力变化、结构损伤的规律。并借助已有实验数据对模拟中LS-DYNA所使用的各种单元及材料本构进行验证，确保本文滚石冲击桥墩的数值模拟结果真实有效。

1 滚石撞击桥墩动力学理论及数值实现方法

滚石撞击桥墩是一个复杂的多重非线性的碰撞动力学问题。当滚石撞击桥墩后桥墩材料和结构都会发生显著的变形，材料也会从线性进入非线性阶段。材料的力学特性在动荷载与静力荷载下有所区别，滚石撞击桥墩作用机理异常复杂，其中涉及材料非线性、几何非线性及边界非线性[7]。碰撞动力学问题与常规静力学问题有着本质不同，碰撞动力学过程不能忽略加载速率、材料应变率、质量惯性力等所造成的影响，因此要研究碰撞动力学问题就需要扎实的理论与深厚的数学功底，但近年来随着计算机技术的发展和有限元理论日趋成熟化，使得数值仿真越来越高效准确可靠。ANSYS/LS-DYNA是一款成熟可靠的非线性显式动力学软件，常常运用到碰撞动力学问题的数值仿真分析中，采用有限元仿真的方法来解决复杂的非线性碰撞问题，是一种相当简便、经济、可靠有效的办法。

1.1 碰撞动力学与静力学分析的差异

目前，针对碰撞动力学问题通常采用拟静力学的分析方法，往往得不到理想的结果。在动荷载作用下结构和材料会发生迅速变形，这一问题就涉及弹塑性及结构动力学的诸多问题。该问题与通常的静力学问题的差异可以从下面3个方面进行阐述：

1.1.1 材料和结构中的应力波

固体处于平衡状态时，当遭受到动荷载冲击打破其原来平衡状态的扰动时，结构中某一点的状态变化是以波的方式传递到其他位置，这种波称为应力波。结构的扰动比较小时产生的波是弹性波，这种情况下材料的变形处于弹性范围内；结构的扰动较大时产生的波是塑性波，这种情况下材料变形会进入到塑性变形阶段。

1.1.2 材料的动态行为

在动荷载作用下，材料的变形速率也会变大，由于材料的变形机制是由其微观结构决定的，材料强度与应变率有一定相关性，通常高变形速率下材料的抵抗能力高于低变形速率下材料的抵抗能力，该结论早已经被众多实验所证实，即所谓的材料动态行为。当材料处在较高速率变形的时候，材料进入塑性阶段发生塑性变形时的材料本构方程如下：

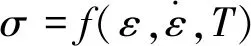
(1)

在较低应变率下，塑性变形的材料本构关系的经验公式符合指数关系的变化，其经验公式为：

σ=σ0+kεn

(2)

经验公式中，σ0为屈服应力，MPa；ε为σ对应的应变；k为硬化系数；n为硬化项系数。

1.1.3 惯性力的影响

当动力载荷超过了静态承载力的时候，此时结构便会产生加速度，由达朗贝尔原理可知，由此产生的惯性力可以承受外荷载，同时外载荷大小也决定加速度的大小，因此惯性力的大小也与之相关，故外载荷较大时，惯性力也就越大，结构短时间内的承载能力将会比静态时的承载能力提高许多。这个特点是结构动力响应分析和静力极限分析的本质区别。

在滚石撞击桥墩结构的撞击过程中，不仅存在弹性变形，也同时存在塑性变形，两种类型的变形以及它们之间的分界面也都随时间而变化。因此分析滚石撞击桥墩接触动力问题时，既要选择合理的动力材料本构模型，也需要恰当处理复杂多变的动力边界问题。

1.2 显式中心差分法数值分析介绍

LS-DYNA是一款成熟可靠的显式动力学分析程序备受世界各地研究者的青睐，由于其可以分析金属成型制造、快速碰撞以及爆炸等一系列非线性动力问题，同时该程序还可以进行传热递、流体问题及流固耦合问题等的求解分析，软件分析结果的准确性与可靠性已经被多次的试验所验证[8]。由于程序能够真实地仿真模拟各种复杂的动力学问题，在实际工程的应用中被广泛认可。ANSYS与LS-DYNA这两款软件是有两个公司分别开发的，1996年，两家公司展开合作才正式推出了ANSYS/LS-DYNA软件，该程序整合了LS-DYNA出色的显式动力学分析功能与ANSYS的可视化快速建模功能，因此使得软件操作使用时十分方便快捷，该软件也逐渐成了研究者最信任的辅助动力学仿真分析工具[9]。

本文拟选用ANSYS/LS-DYNA显式动力学软件进行数值分析，即采用ANSYS作为前处理软件进行APDL参数化有限元几何模型建立，然后让其输出K文件并编辑生成的K文件代码，最后调用ANSYS/LS-DYNA软件中的LS-DYNA子模块求解器进行求解分析，最后利用LS-PREPOST专业后处理程序。

LS-DYNA作为以显式积分求解为主非线性动力学求解软件，本小节将会对显式动力积分的方法给予介绍[10]。

LS-DYNA软件用的是中心差分时间积分的显式方法，计算模型结构中各节点当第n个时间步结束时刻的加速度向量为：

a=M-1[P(tn)-Fint(tn)]

(3)

上述公式中，P为施加的外力向量(包括体力经转化的等效节点力)；Fint为内力矢量，它由下面几项构成：

(4)

公式中的3项依次为：第1项为在当前时刻单元应力场等效节点力(此项对应于动力平衡方程中的刚度项，即单元刚度矩阵与单元节点位移的乘积)；第2项沙漏阻力(该项为克服单点高斯积分引起的沙漏问题而引入的黏性阻力)；第3项接触力矢量。

可以由下面两公式算出节点速度和位移适量：

V(tn+1/2)=V(tn-1/2)+0.5a(tn)(△tn-1+△tn)

(5)

U(tn+1)=U(tn)+V(tn+1/2)△tn

(6)

时间步和时间点的定义为：

△tn-1=(tn-tn-1),△tn=(tn+1-tn)

(7)

tn-1/2=0.5(tn+tn-1),tn+1/2=0.5(tn+1+tn)

(8)

下个增量新的几何构型由初始构型X0加上位移增量获得，即：

Xt+△t=X0+Ut+△t

(9)

上述积分方法是一种显式积分方法，它的基本特点有如下几个方面[11]：

(1)计算过程中不形成总体的整体刚矩阵，弹性项放在内力当中，进而由此避免了矩阵的求逆过程，这特点对非线性分析来说有非常大的意义，因为在计算过程中每个非线性增量步、结构的刚度矩阵都在时刻变化，这样一来减少了大量运算量，节省了时间。

(2)因为当质量矩阵为对角矩阵时，采用上面的递增公式来求解动力运动方程时，就不用进行质量矩阵的求逆运算，仅仅要运用矩阵的乘法进而获得右端的等效荷载向量，因此节省了大量运算，也节省大量计算时间。

(3)上面的中心差分方法是一种条件稳定的算法，若要保持稳定状态需要当前的积分时间步长小于结构计算的临界时间步长。

有关显式中心差分算法的计算稳定性条件，为了确保收敛的临界时间步，因此需要满足如下面的公式：

△t≤△tcr=2/ωn

(10)

公式中，△tcr为时步临界值，△t为每一时刻的时步，ωn为结构系统单元的，下面给出结构系统中最小单元的动力特征值方程：

|Ke-ω2Me|=0

(11)

其中Ke为结构的刚度矩阵，Me为结构的质量矩阵。由此方程便可以得到最大特征值即为ωn。为保证计算收敛，因此LS-DYNA选用变步长积分法，其中每一时刻的积分步长的大小均有当前结构网格中的最小单元尺寸的特征长度决定。

2 有限元建模

2.1 依托工程背景

本文以某山区高速公路三跨先简支后连续梁桥为例，该桥位于山区滚石地质灾害易发区域，上部结构为箱梁，跨径组合为(3×30 m)；滚石为花岗岩，滚石形状取方形滚石；桥墩形式为独柱式墩(或双柱式墩)，桥墩高度(含盖梁)15 m，圆形截面半径为1.0 m，混凝土保护层厚度5 cm，桥墩采用C30混凝土；桥墩纵向配置48根直径28 mm纵筋，螺旋箍筋采用直径为12 mm，钢筋强度等级为HRB335，桥墩顶部、底部加密区长度均为1 m，箍筋加密区间距为100 mm，非加密区间距150 mm；桥墩承台采用矩形承台尺寸(2.6 m×6.8 m×2.5 m)；桩基采用双柱桩基，桩基半径0.8 m，桩基深度20 m；基础土层参考工程地质的实际情况。所建立的模型如图1所示。

下面给出独柱墩、双柱式桥墩的有限元模型建模基本参数，如表1所示：

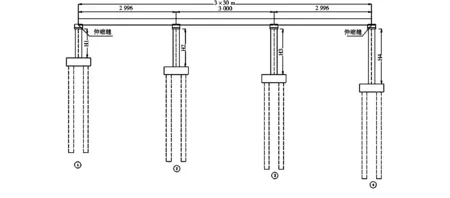
图1 桥型布置示意(单位：cm)Fig.1 The schematic diagram of bridge layout

桥墩高度/m桥墩直径/m纵筋直径/mm纵筋根数纵筋配筋率/%配箍率/%柱桩直径/m桩基深度/m桥墩形式15 2 28 480.930.121.6 20 独柱墩15 1.6 22 360.680.1691.7 20 双柱墩

2.2 有限元模型简化

滚石撞击桥墩的碰撞过程是非常复杂的非线性动力过程，在数值模拟过程中，如果按照实桥建模，则模型单元数太多、计算量过于庞大且计算时间过长、不经济可靠。况且滚石碰撞桥墩过程中，我们仅关心桥墩的动力特性，因此建立有限元模型时可以对模型进行简化处理，对重点研究部位网格精细化分(桥墩部位)，非重点部位的有限元网格可以适当放粗，建出主要部位构件，次要构件简化处理，以达到经济合理的目的。

(1)上部结构的简化处理

通过查阅文献[7,12]可知，在滚石撞击桥墩过程中，上部结构建出(上部结构未简化)、上部结构简化为质量单元附加到盖梁上(上部结构简化)，对比发现两个模型的撞击力变化规律相似，最大撞击力峰值数值上相差不到5.4%，墩顶处最大位移数值上相差不到10.8%，撞击最大深度相差不到2%，由此可知，将上部结构进行简化处理，对数值模拟结果有一定的影响，但影响可以接受，况且将模型进行简化处理之后计算时间大大缩短，因此本文的滚石撞击桥墩数值模拟均采用对上部结构简化处理方法来建模。

上部结构简化，采用MASS166质点质量单元，该单元为集中质量单元，是由一个质量节点和质量值定义，数值模拟仿真时将上部结构作为质量力附加到桥墩顶面，总共388.8 t。

(2)钢筋的简化处理

桥墩建模时，按图纸正常配筋，桥墩纵筋与混凝土采用共节点的连接方式，桥墩的螺旋箍筋，由于螺旋箍筋采用共节点处理工作量大，相对比较繁琐，在LS-DYNA中通过添加关键字，采用“CONSTRAINED_LAGRANGE_IN_SOLID”的方法，将钢筋单元耦合到混凝土单元，即钢筋单元所在从组耦合到混凝土所在主组中。在滚石撞击桥墩有限元仿真中，重点关心的部件是桥墩部件及撞击部位，因此建模时只对桥墩进行的配筋处理，桩基及桥梁承台均未考虑其配筋影响。

(3)桩—土作用及上部结构约束的简化处理

本文研究滚石撞击桥墩过程中，桩—土作用及上部结构约束均采用线性弹簧单元来模拟。文中滚石撞击桥墩有限元模拟时，桩—土作用及上部结构的约束作用均采用COMBI165弹簧阻尼单元来模拟，且采用线性弹簧模型，模拟桩—土作用时未考虑土的塑性变形。

2.3 有限元模型建立

滚石撞击桥墩过程中并不关心滚石的应力变化，因此将滚石定义为刚体，从而节省了计算时间消耗。滚石与桥墩初始间距为100 mm，为了提高有限元计算效率，对上部结构进行简化处理，上部结构以质量单元的形式施加到盖梁顶部；桩-土作用及上部结构约束作用均采用土弹簧来模拟，弹簧一端与桩共用节点，另一端全部约束(即固结)，土弹簧刚度按规范计算得出；由于实际工程中桩基底层为岩石层，因此桩基考虑为端承桩类型，边界条件为桩基底部固结约束；混凝土结构阻尼比取为5%;采用显式动力学软件ANSYS/LS-DYNA展开仿真分析，计算时间步长采用自动时间步长，计算时设置运算截止时间为0.1 s，为运算截止判断条件，有限元模型如下图2～图4所示。

图2 桥墩有限元模型Fig.2 The Bridge finite element model

图3 桥墩钢筋笼有限元模型Fig.3 The Finite element model of bridge reinforcement cage

图4 滚石有限元模型Fig.4 The Rolling Stone Finite Element Model

3 桥墩结构形式对撞击结果的影响分析

山区地形条件复杂，桥梁多建设在微坡、缓坡、陡坡、极陡坡的不同形式边坡上，下部结构不同墩型在西部山区均有广泛应用，但是由于双柱式桥墩整体刚度和抗倾覆稳定性好等优势，在山区的应用越来越普遍。为了探究双柱式桥墩的防滚石撞击性能，本节对山区滚石撞击单柱式、双柱式桥墩进行有限元仿真分析，探究桥墩结构形式受滚石撞击结构响应差异。

为探究滚石撞击不同结构形式桥墩所造成动力响应的差异，本节在保持滚石基本参数一致的前提下，研究因桥墩结构形式不同而造成滚石撞击桥墩动力响应的差异，桥墩结构形式具体参数如表2所示。

表2桥墩结构形式工况参数表
Table2The Parameter table of workingcondition of pier structure

工况滚石质量/t滚石速度/(m·s-1)撞击位置桥墩结构形式工况2510中部独柱墩工况13510中部双柱墩

3.1 撞击力分析

为了研究不同桥墩结构形式在滚石撞击桥墩时撞击力的变化规律。让滚石顺桥向撞击两种不同结构形式的桥墩，探究不同结构形式桥墩受到滚石撞击时，撞击力时程曲线的变化规律。下面给出不同结构形式桥墩滚石撞击力时程曲线及两种不同结构形式桥墩下撞击力峰值表。

图5 不同桥墩结构形式工况撞击力时程图Fig.5 The Time history diagram of impact force conditions of different pier structures

由不同桥墩结构形式工况撞击力时程图可知：由于滚石初始间隙相同，滚石与桥墩的接触碰撞时间相同；不同桥墩结构形式工况下撞击力F(t)随时间变化趋势一致，撞击力时程呈现一个类似三角形脉冲荷载，持续时间为t，该阶段荷载作用时间较短，但荷载峰值较大；滚石撞击双柱式桥墩时撞击峰值比撞击独柱式桥墩时稍低。

表3不同桥墩结构形式工况撞击力最大值表
Table3The Maximum value of impact force ofdifferent pier structures

工况撞击力峰值/MN 工况2(独柱墩)18.834 工况13(双柱墩)17.235 相对差值/%9.28

由不同桥墩结构形式撞击力最大值表3可知：工况2即独柱墩结构形式最大撞击力比工况13双柱式桥墩结构形式的最大撞击力稍大，相对差值为9.28%；不同桥墩结构形式工况受到相同滚石撞击时，由于独柱式桥墩比双柱式桥墩刚度更大，使得独柱式桥墩滚石的最大撞击力稍大。

3.2 位移分析

为了探究不同桥墩结构形式受到相同滚石参数撞击下结构动力响应，分析桥墩撞击处和桥墩顶部位置的位移时程变化规律。下面给出关键部位节点位移时程图及关键部位节点最大位移值表格。

附注8：7 906点为盖梁顶部左端节点；7 752点为盖梁顶部中间节点；7 699点为盖梁顶部右端节点；145 919点为撞击位置中心节点。

图6 关键节点位置示意图Fig.6 The Schematic diagram of key node locations

由墩顶节点位移时程图可知：双柱式桥墩墩顶部位7 699节点、7 752节点、7 906节点的节点位移在撞击发生后均先朝着撞击反方向增大后朝着撞击方向增大到最大值；盖梁顶部3个节点位移的最大值不同，由于7 699节点位于滚石所撞击侧桥墩的顶部，因此7 699节点位移最大；由于双柱式桥墩盖梁、底系梁的存在使整个桥墩结构形成一个框架，双柱式桥墩在滚石撞击一侧桥墩后，桥墩结构有横向扭转的现象，这与桥墩顶部3个节点位移的变化差异相符合；从桥墩撞击部位节点位移时程曲线可知，节点位移随着时间变化规律呈现周期交替趋势，由于阻尼的存在，其峰值逐渐衰减，由于计算时间受限变化规律并不是十分显著。

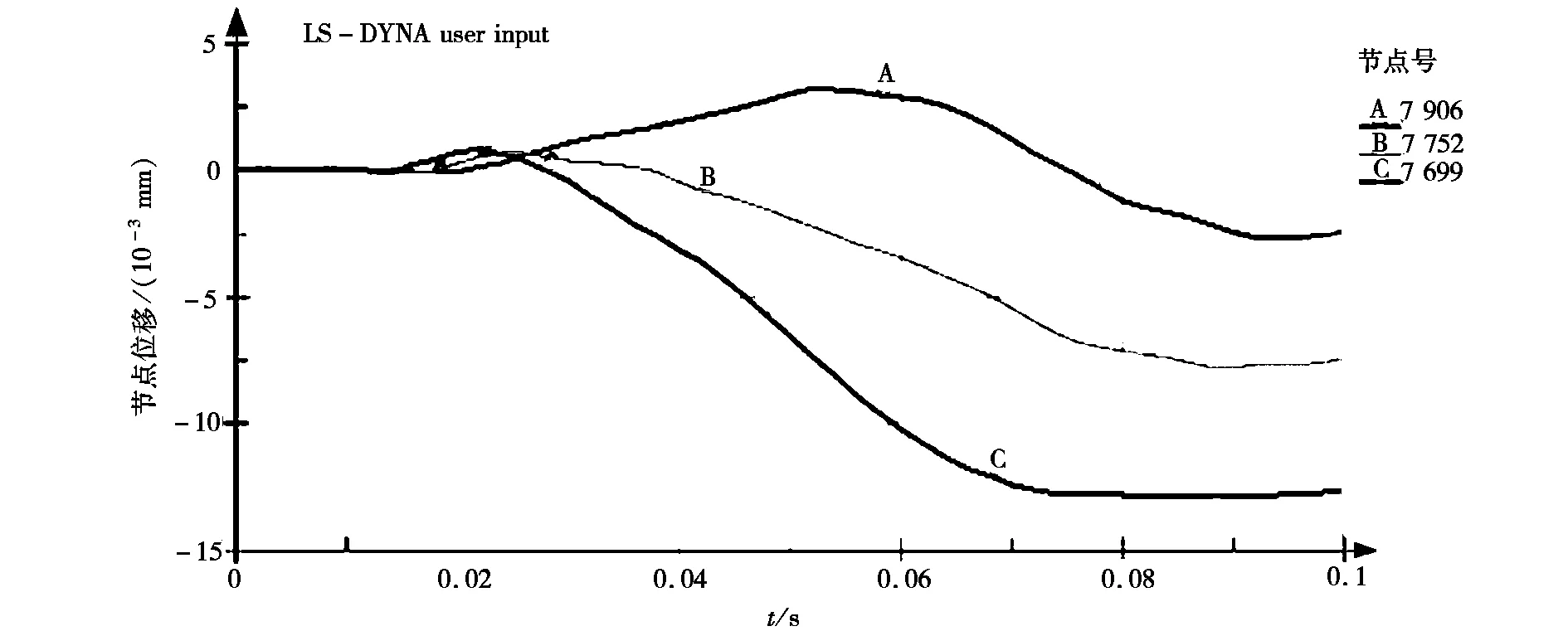
图7 墩顶部位节点位移时程图Fig.7 The Time history diagram of the displacement of the top node of the pier

图8 撞击部位(145 919节点)节点位移时程图Fig.8 The Time history diagram of the node displacement at the impact location (145 919 nodes)

下面列出双柱式桥墩结构滚石撞击下关键部位节点位移的最大值，如表4所示。

表4关键部位节点位移最大值
Table4The Maximum displacement of key parts mm

节点号 节点位移Y轴正向Y轴负向7 6990.862-12.9017 7520.723-7.7507 9063.236-2.691145 9190.796-20.841

由节点位移最大值表可知：滚石撞击双柱式桥墩时，滚石撞击侧桥墩顶部位置节点(7 699节点)位移值最大为12.901 mm，盖梁中间节点(7 752节点)及另一侧桥墩顶部节点(7 906节点)位移最大值依次减小，双柱式桥墩结构有扭转的趋势；由于双柱式桥墩结构的刚度较独柱式桥墩弱，在滚石撞击双柱式桥墩结构时，撞击部位最大节点位移为20.841 mm。

下面列出不同墩柱结构形式下工况2(独柱式桥墩)与工况13(双柱式桥墩)关键部位节点位移最大值对比表如表5。

表5关键部位节点位移最大值表
Table5The Maximum table of key node displacement mm

工况墩顶位置节点位移撞击位置节点位移Y轴正向Y轴负向Y轴正向Y轴负向工况20.615-7.034\工况130.862-12.9010.796-20.841

由不同桥墩结构形式工况下关键部位节点位移最大值表可知：由于双柱式桥墩结构较独柱式桥墩结构“柔”，在相同滚石参数下双柱式桥墩结构墩顶位移较大；由于独柱式桥墩结构刚度较大，在滚石撞击瞬间撞击部位中心处单元失效，其单元所属的节点也随之失效，而双柱式桥墩结构刚度较小表现的较“柔”撞击部位中心处单元并未失效，撞击部位中心处节点位移最大为20.841 mm。

3.3 桥墩钢筋应力分析

桥墩纵筋的应力集中出现在撞击侧桥墩的撞击处附近，纵筋的最大拉应力出现在撞击侧桥墩背部达到206.9 MPa，并未达到钢筋的屈服强度；螺旋箍筋的最大应力同样出现在撞击侧桥墩撞击处附近，螺旋箍筋的最大拉应力达到336.8 MPa，达到箍筋屈服强度，撞击处螺旋箍筋有一定的塑性变形；钢筋与混凝土仍能正常粘结，共同发挥作用。

下面列出不同桥墩结构形式工况下，桥墩纵筋及螺旋箍筋最大应力值表如表6。

表6不同桥墩结构形式桥墩钢筋最大应力表
Table6The Maximum stress table of bridge piers indifferent pier structures MPa

工况桥墩钢筋应力纵筋应力螺旋箍筋应力工况2137.2 148.6 工况13206.9 336.8

由桥墩钢筋应力表可知：在相同的滚石参数条件下，滚石撞击双柱式桥墩钢筋的应力较独柱墩大；由于双柱式桥墩结构比独柱式桥墩结构的刚度小，因此在滚石撞击时双柱式桥墩的混凝土保护层相对独柱式桥墩结构显得更薄弱些。

3.4 损伤分析

下面给出不同桥墩结构形式工况下桥墩损伤情况统计表如表7。

表7桥墩损伤情况统计表
Table7The Statistics on damage of bridge piers

工况混凝土损伤面积/cm2撞击最大深度/cm混凝土失效体积/cm3体积损失率/%工况24 055.835.21321 143.040.051 8%工况136 852.455.78639 648.270.147 2%

由不同桥墩结构形式桥墩损伤情况统计表可知：双柱式桥墩结构与独柱式桥墩相比，桥墩混凝土损伤面积、最大撞击深度、混凝土损失体积、体积损失率均随之增加；由于双柱式桥墩较独柱式桥墩刚度小，当滚石撞击双柱式桥墩时损伤更严重些；在工况13时，滚石撞击桥墩的最大撞击深度达5.786 cm，损伤已经达到核心混凝土部位，不过核心混凝土损伤较小，并未造成非常严重的损伤，但对钢筋混凝土桥墩的结构承载能力有所影响。

4 结论

本章通过有限元仿真对山区滚石撞击桥墩影响参数展开分析，研究探讨了滚石质量、滚石撞击角度对桥墩结构动力响应的影响，得出如下结论：

(1)通过对滚石撞击桥墩有限分析可知，山区滚石撞击桥墩对桥墩的损伤主要集中在滚石撞击区域范围内，以局部损伤破坏为主。

(2)在其它因素基本一致的前提下，通过改变桥墩的结构形式，探讨独柱式桥墩与双柱式桥墩的差异，发现滚石顺桥向撞击时独柱式桥墩的滚石撞击力比双柱式的撞击力大9.28%；

(3)通过分析可以发现，双柱式桥墩的位移响应、钢筋应力、桥墩损伤指标都比独柱式桥墩表现的显著。

本文仅对桥墩结构单一因素影响下的滚石撞击结构响应进行了分析，下一步可对滚石撞击桥墩时滚石参数进行分析，参考笔者分析方法进行研究。