平面关节型机械手的运动学求解与仿真研究

傅永建,张雪华,丘友青

(1.龙岩学院 机电工程学院,福建 龙岩 364012； 2.龙岩技师学院,福建 龙岩 364000)

平面关节型机器人[1-2]具有装配机器人需要的柔性关节手臂，表现为水平方向上具有较好的柔顺性，垂直方向上拥有较大的刚性，具有结构简单、动作灵活的优点，被广泛应用于装配作业活动[3]。对平面关节型机械手进行运动学分析，有助于其伺服电机的选择，为控制系统的设计和研发提供参考和决策依据。

1 平面关节型机械手结构

平面关节型机械手实物图如图1所示，由一个移动关节和两个旋转关节组成。移动关节主要控制机械手手腕的伸缩，旋转关节分别控制机械手的抓合和机械大臂和小臂的旋转[4]。其实物简化图如图2所示。

图1 平面关节型机械手实物图Fig 1 Physical map of plane joint manipulator

1—机械手机身；2—大臂电机；3—光电编码器；4—大臂； 5—小臂电机；6—同步带；7—小臂；8—手腕升降电机； 9—手爪电机；10—手抓；11—光电编码器。图2 平面关节型机械手简化图Fig 2 Schematic diagram of plane joint manipulator

平面关节型机械手的各关节均选择直流电机作为驱动装置，在两个旋转关节上装有增量式光电编码器，主要用来提供半闭环控制所需要的反馈信号。

2 机械手运动学方程

机器人机械手的运动学方程，就是机械手的每个组成杆件相对于基础坐标系在空间中的位置和姿态的方程[5]。为实现平面关节型机械手每个杆件空间位置的描述，采用杆件坐标系，将机座视为机械手臂首端杆，末端执行器视为末端杆。

若平面关节型机械手由n个杆构成，杆件编号依次为0，1，2，3，，n，那么机械手的变换方程[6]

(1)

(2)

公式(2)表示平面关节型机械手的运动学方程，描述了关节变量和末端杆的位置之间的关系。

2.1 运动学方程的正解

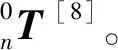
A矩阵的参数如表1所示，其中αi和ai分别为初始位置的角度和长度。

(3)

图3 平面三杆机械手坐标系Fig.3 Coordinate system of plane three-bar manipulator

表1机械手的结构参数表
Table1Structure parameter table of manipulator

杆件号i关节变量αi/(°)ai/mcos αisin αi100l1+xl102θ10l2103θ20l310

(5)

推出：

(6)

式中：c12=cos(θ1+θ2)；s12=sin(θ1+θ2)；c1=cosθ1；s1=sinθ1。

2.2 运动学方程的逆解

机械手运动学逆解问题，就是已知满足某工作要求时末端执行器的空间位置，求解关节变量[9]。

已知：

(7)

(9)

联合公式(8)、公式(9)，推导出公式(10)[10]：

(10)

当机械手工作时，其末端位置由公式(10)推出，机械手末端位置如图4所示。

图4 机械手末端位置图Fig 4 Terminal position map of manipulator

因θ1+θ2=90°，则c12=cos(θ1+θ2)=0；s12=sin(θ1+θ2)=1，故公式(10)变为：

(11)

则

(12)

3 实验仿真

为实现机械手的运动学求解，运用MATLAB机器人工具箱进行平面关节型机械手的运动学仿真。平面关节型机械手的仿真模型如图5所示。

图5 平面关节型机械手仿真模型(单位：m)Fig 5 Simulation model of planar articular manipulator

通过机器人工具箱控制面板，设置平面机械手的初始位置和旋转角度，结合图6设置关节变量参数和位置状态，实现图7机械手的位置、加速度和速度变化曲线的获取，为机械手的空间规划和平面布局提供参考依据。通过机械手正运动学和逆运动学分析，获得雅克比矩阵，进而通过雅克比矩阵实现当前位置、速度的正向分析和逆向分析；根据机械手手爪初始位置坐标和机械手空间参数，获得关节扭矩和角速度曲线，从而与当前位置、速度的正向分析和逆向分析一起为伺服电机的选择、控制系统的设计和研发等提供参考和决策依据。

图6 正运动学和逆运动学求解Fig 6 Solution of forward kinematics and inverse kinematics

图7 位置、加速度和速度曲线Fig 7 Position, acceleration and speed curves

4 结论

为实现平面关节型机械手伺服电机的合理选择，根据平面关节型机械手的结构特征建立其运动学模型；在机械手正运动学和逆运动学的数学模型基础上，建立平面关节型机械手模型并进行仿真，获得关节扭矩和角速度曲线，从而与当前位置、速度的正向分析和逆向分析一起为伺服电机的选择、控制系统的设计和研发提供参考和决策依据。