基于响应面法的基坑支护结构稳定可靠度分析

廖 瑛,樊伯旺

(苏州科技大学 土木工程学院，江苏 苏州 215011)

基坑工程是一项理论与实践相结合的岩土工程，也是一项风险大、难度大、投资高的基础性工程。为了确保基坑工程在施工过程中的稳定并将周围土体的变形控制在一定范围内，在场地受限的开挖范围内必须要对坑壁进行有效的支护和加固，因而基坑支护结构的稳定性研究是一项重要的课题。目前，基坑支护结构稳定性与变形的验算方法主要采用定值的安全系数法[1]，即将抗力效应与荷载效应的比值作为安全系数来衡量结构的安全程度。由于这种方法将土体视作均匀介质，没有考虑到如土体抗剪强度指标、地下水埋深、土层厚度及重度等都是随时空变化的、都不可避免地具有随机性和变异性等不确定性特点，因而安全系数法并不能客观、合理地反应基坑支护结构实际的安全程度。而基于概率论与数理统计的结构可靠度理论充分考虑了计算参数的不确定性特点，可以采用响应面法、一次二阶矩法、蒙特卡罗法、优化算法等方法计算结构的可靠指标及失效概率，利用概率定量地度量结构的可靠性[2-6]，较之于安全系数法可以做到更加科学、全面地对工程结构的可靠性作出判断。

1 响应面法

当基本随机变量对系统的响应不能建立明确的表达式反应它们之间的映射关系时，就需要利用响应面法拟合一个响应面来模拟实际问题的功能函数。响应面函数的建立是响应面法的关键，它应在描述真实情况的前提下做到尽可能的简单，在结构可靠度分析时一般常取为二次多项式形式：

(1)

式中，Xi为基本随机变量；a、bi、ci为(2n+1)个待定系数。该方法的计算步骤为：

(1)假设初始迭代点X=(X1,X2,,Xn)T，一般取基本变量的均值μX。

(2)通过数值方法计算功能函数值g(X1,X2,,Xn)以及g(X1,X2,,Xi±fσi,,Xn),其中系数因子f在第一步迭代中取为3，之后取为1。

(3)解线性方程组得到2n+1个待定系数，从而确定拟合的响应面函数。

(4)用一次二阶矩法求得验算点X*及可靠度指标β(k)。

(5)将可靠指标β(k)与上一次得到的可靠指标β(k-1)的差值取绝对值并控制在给定的精度范围之内，若精度不满足，则通过式(2)插值得到新的迭代点X，重新计算第2～第5步，直至满足精度要求为止。

(2)

2 基坑支护结构的稳定性验算模式

2.1 基坑支护结构抗倾覆稳定可靠度分析

悬臂式挡土桩、墙、单支撑式挡土墙及土钉支护往往需要做抗倾覆稳定性验算。当基坑开挖后，土体的一侧临空，基坑土体不能依靠自身材料的抗剪强度维持稳定，有向临空面倾覆的趋势。悬臂式基坑支护结构依靠坑底以下的嵌固深度，利用悬臂部分阻止临空土体向基坑方向的倾覆，承受了墙后的主动土压力。墙前被动土压力对转动点的抗倾覆力矩和墙后主动土压力对转动点的倾覆力矩构成了抗倾覆稳定性计算的功能函数：

g(R,S)=MR-MS

(3)

式中：MR为抗倾覆力矩,kN·m/m;MS为倾覆力矩,kN·m/m。

对于悬臂式基坑支护结构，转动点取在墙脚处；对单(多)支点式支护结构，转动点取在最下道支撑处。对于重力式基坑支护结构和土钉墙，还应考虑墙体自重对转动点的抗倾覆力矩。

2.2 基坑支护结构抗坑底隆起稳定可靠度分析

基坑抗坑底隆起稳定可靠度分析，在此采用同时考虑土黏聚力c和内摩擦角φ作用的抗隆起验算法。其抗隆起失稳的功能函数为：

g=γDNq+cNc-[γ(H+D)+q]

(4)

式中：γ为桩底土重度，kN·m-3;c为桩底土黏聚力,kPa;D为支护结构嵌固深度,m;H为基坑开挖深度,m;q为地面超载,kPa;Nq、Nc为地基承载力系数，可以按照Prandtl或者Terzaghi[7]公式确定，在此选择Prandtl公式：

(5)

(6)

式中，φ为土的内摩擦角，(°)。

2.3 基坑支护结构抗滑移稳定可靠度分析

按照传统的安全系数法，重力式水泥土桩墙抗滑移稳定性的安全系数可表达为：

(7)

式中:Ep为被动土压力,kN/m;Ea为主动土压力，kN/m;W为墙体自重,kN/m;μm为水泥土墙底面以上水压力,kPa(若水泥土墙在地下水位以上,取μm=0)，B为墙体宽度,m。

故此，根据结构可靠度理论，基坑支护结构抗滑移稳定性分析的功能函数可以取为：

g=Ep+(W-μmB)tanφ+cB-Ea

(8)

3 工程实例

3.1 工程概述

某基坑[7]开挖深度H=3.8 m，嵌固深度D=4.2 m，地面超载q=20 kPa，桩体自重γ=19 kN/m3，桩宽1.6 m。采用水泥土搅拌桩重力式支护结构，其计算简图及相关土层参数实测表如图1及表1所示。

图1 基坑支护结构计算简图Fig.1 The calculation diagram of the foundation pit supporting structure

表1相关土层参数实测表
Table1The measured table of the relatedsoil layer parameter

土层名称层厚/m重度/(kN·m-3)黏聚力/kPa内摩擦角/(°)粉质黏土317.81816淤泥质黏土318.21514淤泥质黏土218.21314

3.2 计算假定

鉴于工程实际情况的复杂性，在满足一定计算精度的前提下为简化计算，在可靠度计算中作了如下处理：

(1)对于几何尺寸，比如开挖深度H、嵌固深度D等视作常量；土体参数中，土重度γ的变异性较小，故视土体重度γ为常量，仅将土体黏聚力c、内摩擦角φ作为随机变量，并且假定它们均服从正态分布。

(2)对土层各参数均值做加权平均处理以简化可靠度计算过程，至于随机变量的变异系数，鉴于c、φ变异系数的取值范围通常在0.1～0.4[8]，本文取c的变系数为0.20、φ的变异系数为0.25，加权平均处理后的参数均值及随机变量的变异系数如表2所示。

(3)将变量视为独立的随机变量、即不考虑随机变量之间的相关性。

表2土层计算参数表
Table2Table of soil layer calculation parameter

黏聚力c/kPa内摩擦角φ/(°)土重度γ/(kN·m-3)均值μ15.6314.7518.05变异系数δ0.200.25—

(4)一般来说，基坑支护工程是临时性工程，不仅需要考虑基坑支护结构的安全性，还应在满足结构预定功能的前提下考虑工程的经济性，尽可能减少不必要的支出和浪费。通常是采用目标可靠指标来平衡可靠性与经济性这一对相矛盾的目标，因而目标可靠指标的确定是一个相当敏感的问题，在岩土工程中还没有统一的规定。根据文献[8]，当计算变形时规定目标可靠指标β0可取0.85；当计算地基承载力时规定可靠度β0可取0.95，鉴于此本文建议基坑支护结构稳定性验算的目标可靠指标取1.5，相应的目标失稳概率为6.68%。当然在基坑施工中还应充分运用各种现代的方法和手段对施工过程做到实时把控，当发现隐患和危险时更要及时处理以切实保证基坑工程的稳定性。

3.3 稳定可靠度计算结果及结果分析

根据响应面法，采用MATLAB编程计算该重力式基坑支护结构抗倾覆、抗坑底隆起、抗滑移的可靠指标及失稳概率，相关计算结果列于表3中。为便于比较，结构可靠度计算中另一种常用的一次二阶矩法的计算结果也如表3中所示。

表3稳定可靠性计算结果
Table3The calculation results of the stable reliability

稳定性验算模式抗倾覆抗坑底隆起抗滑移响应面法一次二阶矩法响应面法一次二阶矩法响应面法一次二阶矩法迭代次数446745可靠指标1.786 9961.786 9933.505 4213.505 7762.521 0972.521 099失效概率/%3.696 9053.696 9240.022 7940.022 7630.584 9460.584 943验算点坐标(c/kPa,φ/rad)(11.465 284,0.180 702)(11.459 899,0.180 827)(11.440 072,0.048 973)(12.579 936,0.039 197)(11.081 008,0.124 887)(11.071 216,0.125 030)

由表3计算结果可见，响应面法与一次二阶矩法两种计算方法的结果几近相等，在迭代次数上前者等于或少于后者，说明响应面法在重力式基坑支护结构的稳定可靠度计算方面还是比较高效的。由支护结构的3种稳定性验算模式的响应面法计算结果可见，抗倾覆模式的可靠指标最小、为1.786 996，相应的失效概率最大、为3.696 905%，但相较于目标可靠指标1.5及目标失稳概率6.68%，该基坑抗倾覆稳定性是符合要求的，此外抗坑底隆起和抗滑移稳定性也都能够满足目标可靠度的要求，说明该重力式基坑支护结构不会发生倾覆、坑底隆起和滑移破坏，这与工程实际情况是相吻合的。

结构可靠度计算中随机变量参数的变异系数、均值等对结果的影响很大，此外随机变量之间的相关性也会对结果产生影响，故以下对响应面法的计算结果作进一步的探讨以寻找相关规律。

3.3.1 随机变量变异性对可靠度计算结果的影响分析

随机变量变异性对于结构可靠度的计算结果会产生非常大的影响，根据响应面法计算，土体黏聚力c、内摩擦角φ变异系数对于3种基坑支护结构稳定验算模式可靠指标的影响如图2所示。

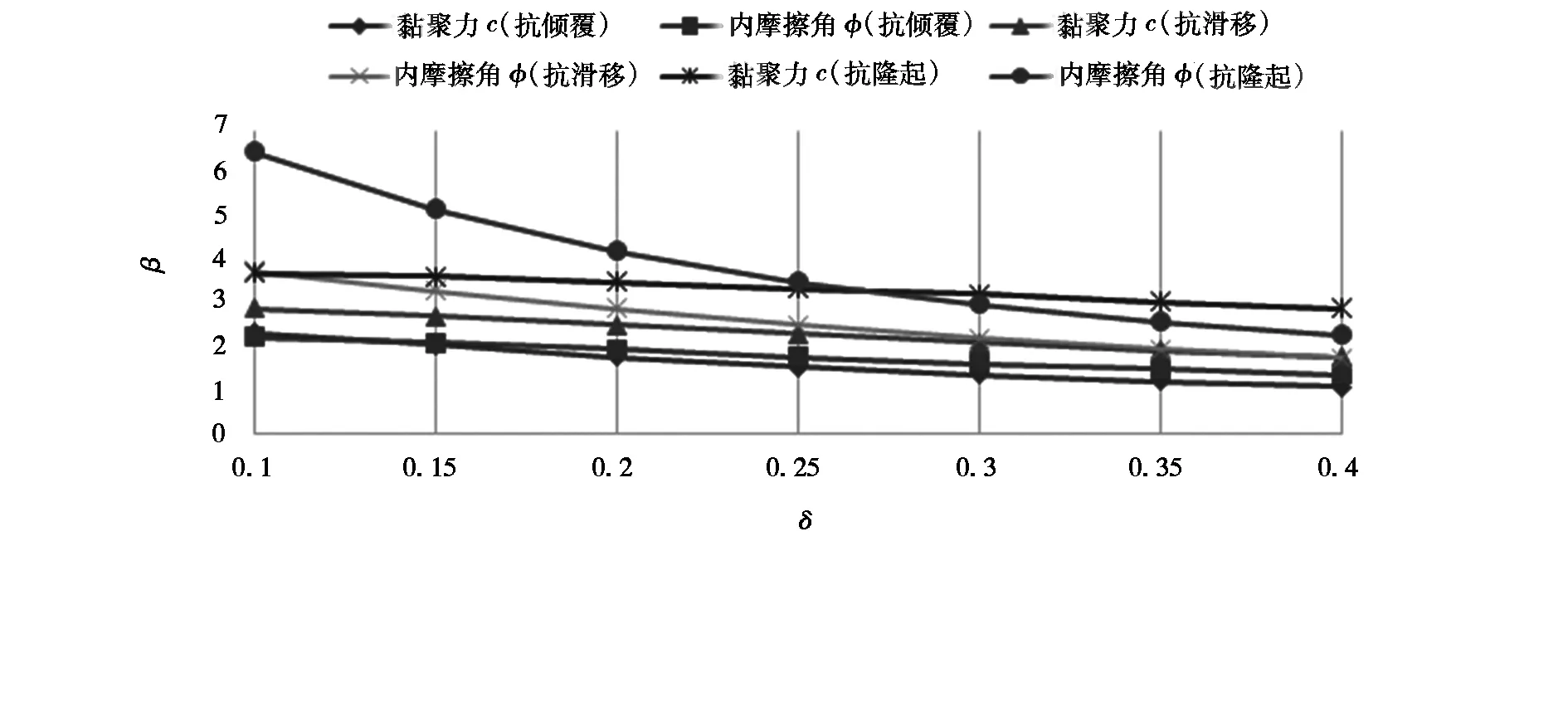
图2 可靠指标β与变异系数δ关系曲线Fig.2 The relation curve between reliability index β and variation coefficient δ

由图2可见，在该重力式基坑支护结构的3种稳定性验算模式中，可靠指标均随着变异系数的增大而减小；在抗倾覆稳定性模式中，c、φ变异系数对于可靠指标的影响相当；但在抗滑移和抗坑底隆起两种稳定性模式中，φ变异系数对于可靠指标的影响明显高于c变异系数对于可靠指标的影响，这种趋势在抗坑底隆起稳定性计算中更为明显，说明内摩擦角的变异性对于可靠度计算的影响甚大，在确定内摩擦角的变异系数时要谨慎。

3.3.2 随机变量均值对可靠度计算结果的影响分析

分别改变随机变量土体黏聚力c和内摩擦角φ的均值，计算三种稳定性验算模式的可靠指标，计算结果如图3、图4所示。

由图3、4可见，可靠指标均随着c、φ均值的增大而增大，其中可靠指标与c均值近似呈线性关系，而可靠指标与φ均值近似呈抛物线关系；此外，在3种稳定性验算模式中，c和φ的均值都对抗倾覆可靠指标的影响最大，鉴于前述计算中抗倾覆稳定性的可靠指标最小，随机变量的均值能极大地影响抗倾覆稳定可靠度的计算结果，故在确定随机变量的均值时尤需慎重。

3.3.3 随机变量相关性对可靠度结计算结果的影响分析

在以上计算中，都是将c、φ视为独立的随机变量进行分析，文献[9]指出，土的c、φ指标之间存在着较强的负相关性，且相关系数ρ通常在-0.8～-0.6变化。在此采用正交变换法[10]来处理相关随机变量，经过变换处理后得到独立的随机变量c′，φ′，它们的均值和均方差可按照式(9)计算。

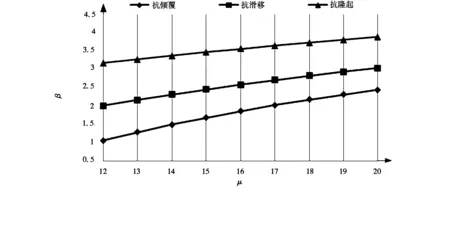
图3 可靠指标β与C均值μ关系曲线Fig.3 The relation curve between reliability index β and C′s mean value

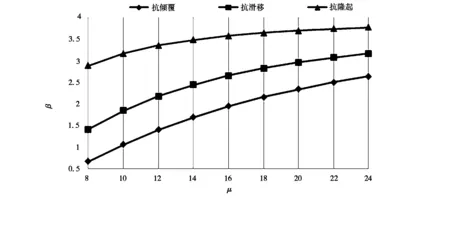
图4 可靠指标β与φ均值关系曲线Fig.4 The relation curve between reliability φ index β and φ′s mean value

(9)

式中，μc和μφ为相关随机变量的均值、σc、σφ为相关随机变量的均方差，ρ为相关系数，σtanφ、μtanφ可按式(10)计算。

(10)

考虑随机变量的负相关性，当将相关随机变量作如上处理变换成独立的随机变量c′，φ′后，即可按照前述响应面法计算结构的可靠指标及失稳概率。该重力式基坑支护结构3种稳定性验算模式的可靠指标与相关系数的关系曲线如图5所示。

图5 可靠指标β与相关系数ρ关系曲线Fig.5 The relation curve between reliability β index and correlation coefficient ρ

由图5可见，在考虑参数间的相关性后，3种稳定性验算模式的可靠指标均明显大于前述不考虑参数间相关性的可靠指标，即不考虑参数间的相关性是偏于保守和安全的，由此说明在实际计算中为简化计算过程，将随机变量视为独立的随机变量是可行的。此外，随着相关系数的增大，可靠指标均呈递减趋势。其中抗倾覆可靠指标受相关系数的影响最大、相关系数对抗滑移可靠指标的影响次之、对抗隆起可靠指标的影响最小。

4 结论

本文根据结构可靠度理论，采用响应面法对一重力式基坑支护结构进行了抗倾覆、抗滑移和抗坑底隆起稳定可靠度分析，并与结构可靠度计算中常用的一次二阶矩法的计算结果进行了比较，主要结论如下：

(1)采用响应面法计算基坑支护结构稳定可靠度是可行的，并且相较于一次二阶矩法，响应面法计算过程简单，收敛速度快，计算精度也能得到保证。

(2)在仅将土体黏聚力c和内摩擦角φ视作随机变量时，基坑支护结构的可靠指标均随着c、φ变异系数的增大而减小，且φ变异系数对于可靠指标的影响更为显著；随着c、φ均值的增大，可靠指标呈递增趋势，其中可靠指标与c均值近似呈线性规律变化、可靠度指标与φ均值近似呈抛物线型规律变化。

(3)当考虑随机变量之间的负相关性时，可靠指标明显大于不考虑变量之间相关性的可靠指标，并且随着相关系数的增大可靠指标逐渐减小。这说明在计算中将随机变量视作独立的随机变量进行可靠度分析既是简单的也是偏于保守和安全的。