需要添加辅助线求解吗？

江苏省南京金陵中学河西分校

李玉荣 (邮编：210019)

问题(2017武汉)如图，△ABC内接于⊙O，AB=AC,CO的延长线交AB于点D．

(1)求证：AO平分∠BAC；

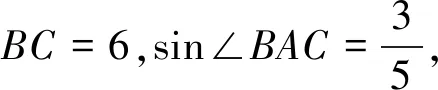
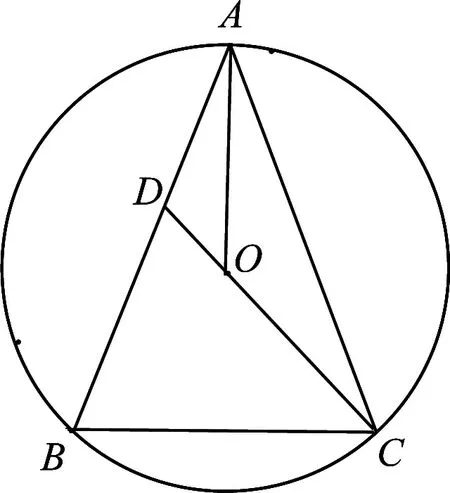
图1

解法1(1)如图1，延长AO交BC于点H，连接OB,

因为AC=AB，OB=OC，所以点A、O在BC的垂直平分线上，

所以OA⊥BC，又AC=AB，所以AO平分∠BAC；

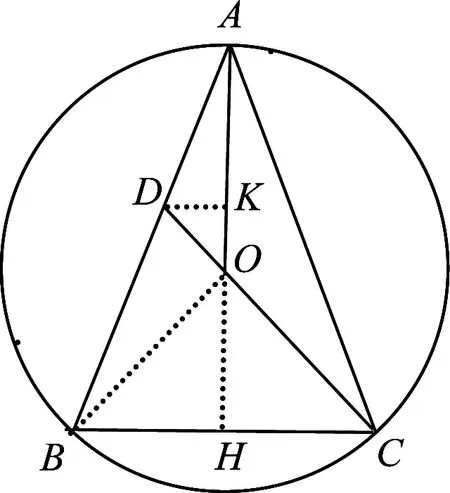
图2

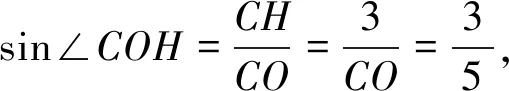
所以AH=AO+OH=9，

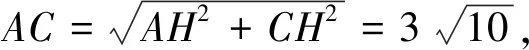
由(1)知，∠BAH=∠CAH，

设DK=3a，则AK=9a，

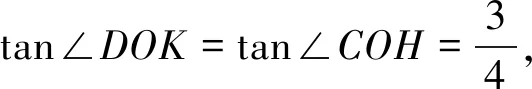
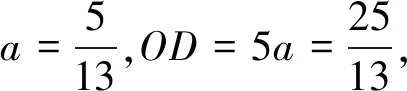
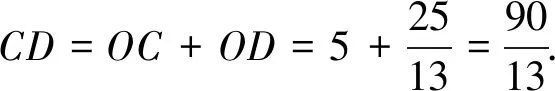
此题的难点是求CD的长，类似的，先给出求CD的第2种解法：

图3

解法2如图3，作DK⊥BC于点K，

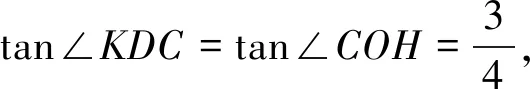
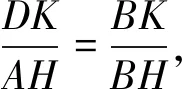
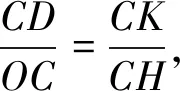
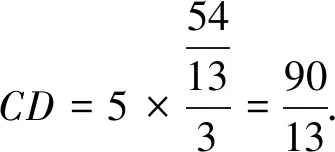
评注这两种解法添加的辅助线为DK⊥AH(DK⊥BC)，从本质上看是DK∥BC(DK∥AH)构造“A型”或“X型”相似三角形，但图中的点D是“未定点”(AD、BD、OD、CD均为未知数)，且所添的辅助线破坏了已知的AO(BH)，导致解题过程较为复杂，为何不从另外的五点A、B、H、C、O添加辅助线入手呢？

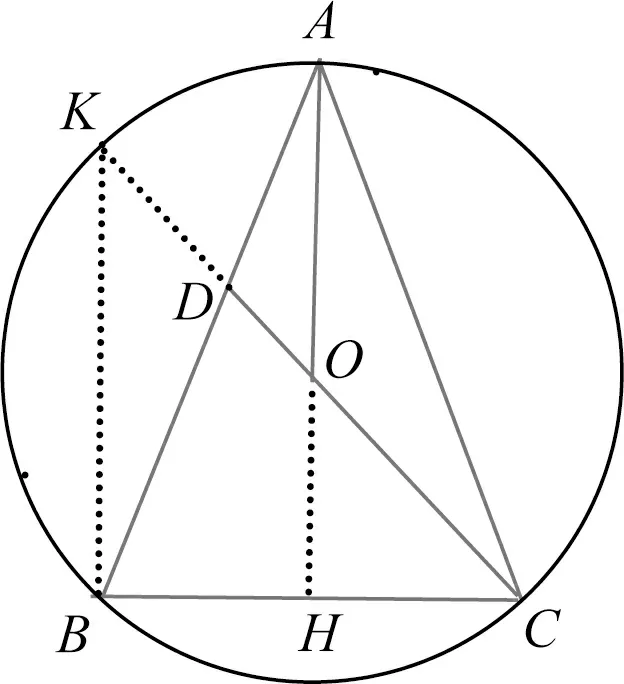
图4

解法3如图4，延长CO交⊙O于点K，连接BK，则BK=2OH=8，且BK∥AH，

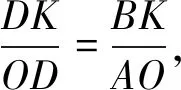
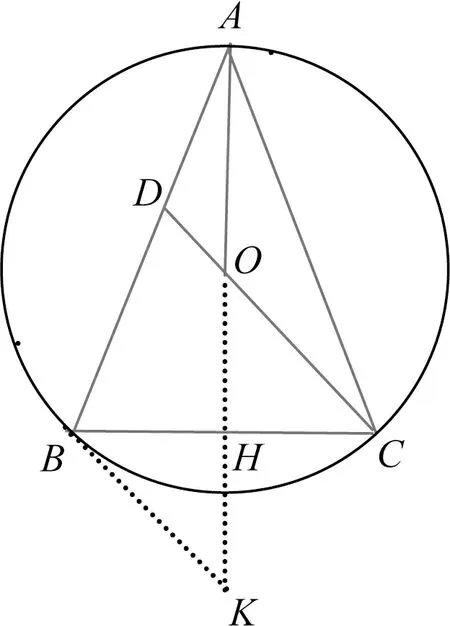
图5

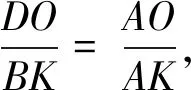
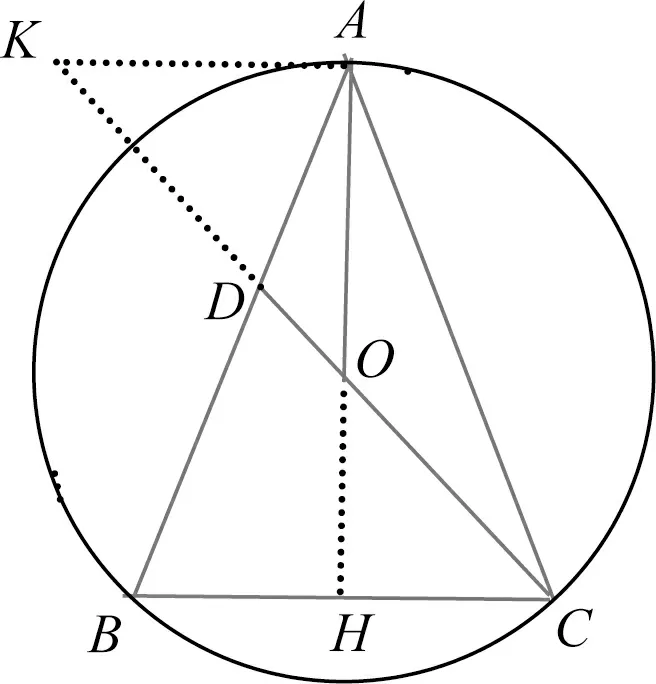
图6

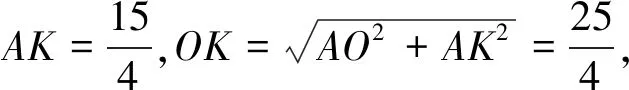
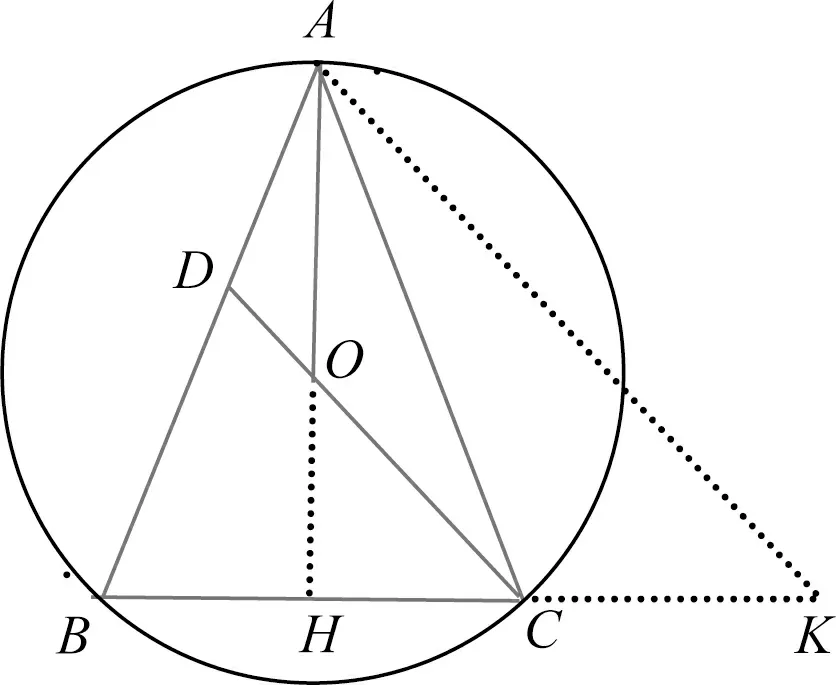
图7

解法6如图7，作AK∥DC交BC延长线于点K，因为AK∥OC，所以△AHK∽△OHC，

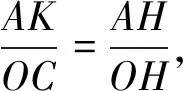
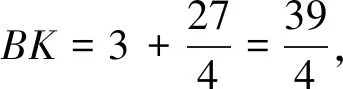
因为AK∥DC，所以△ABK∽△DBC，

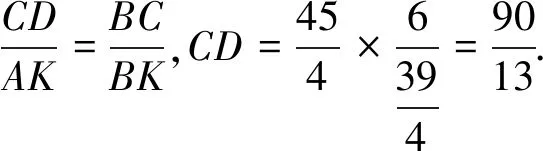
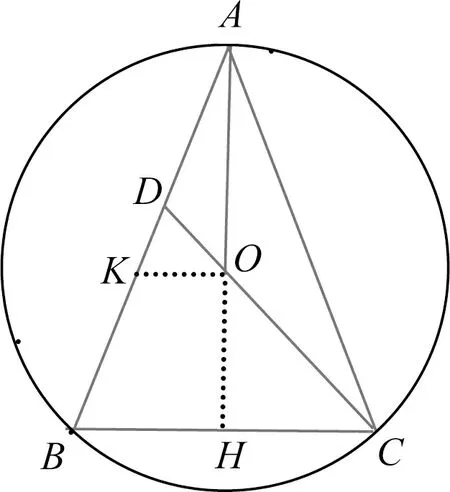
图8

解法7如图8，作OK∥BC交AB于点K，

因为OK∥BH，所以△AOK∽△ABH，

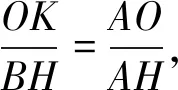
因为OK∥BC，所以△DOK∽△DBC，所以

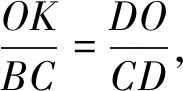
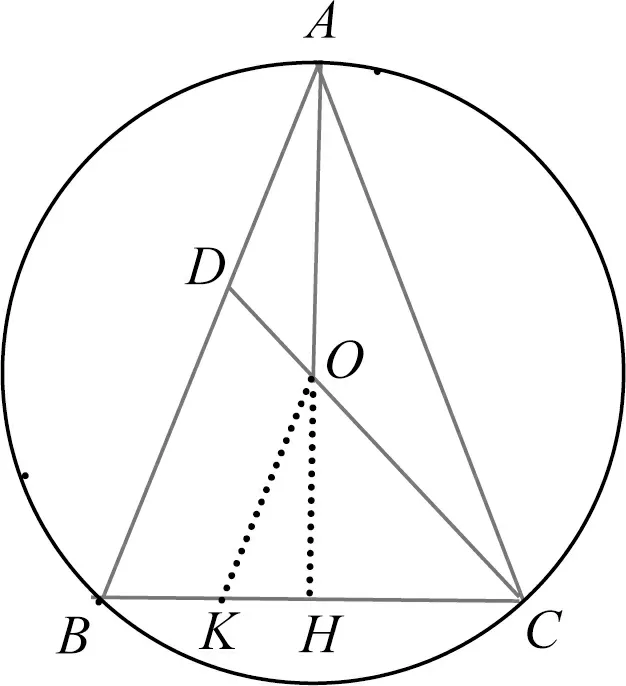
图9

解法8如图9，作OK∥AB交BC于点K，

因为OK∥AB，所以△HOK∽△HAB，

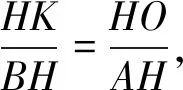
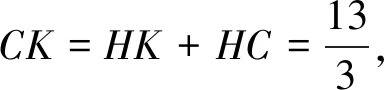
因为OK∥BD，所以△COK∽△CDB，

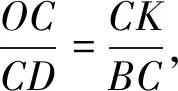
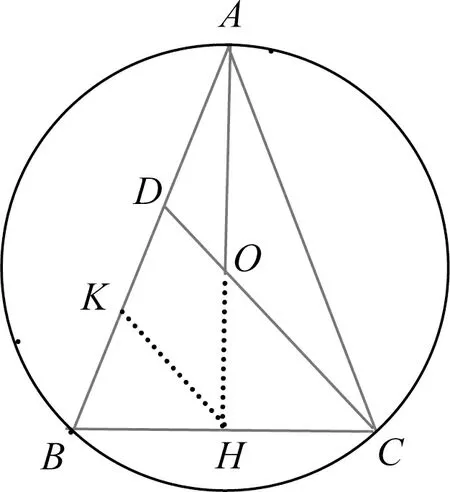
图10

解法9如图10，作HK∥CD交AB于点K，

因为HK∥DO，所以△ADO∽△AKH，

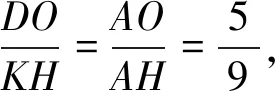
所以△HKB∽△CDB，

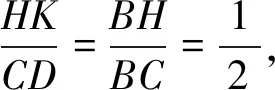
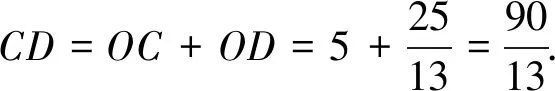
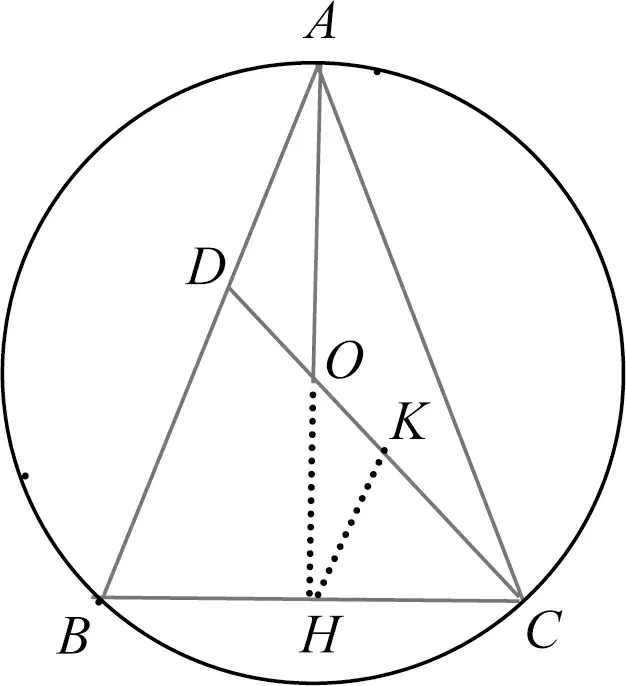
图11

解法10如图11，作HK∥AB交CD于点K，

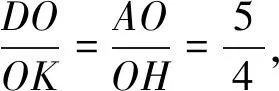
因为HK∥BD，所以△HKC∽△BDC，

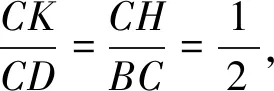
图12

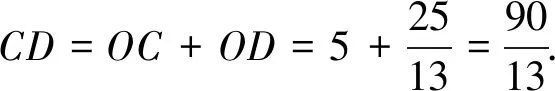
解法11如图12，作CK∥AB交AH延长线于点K，显然△BHA≌△CHK(AAS)，所以HK=AH=9，

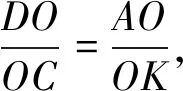
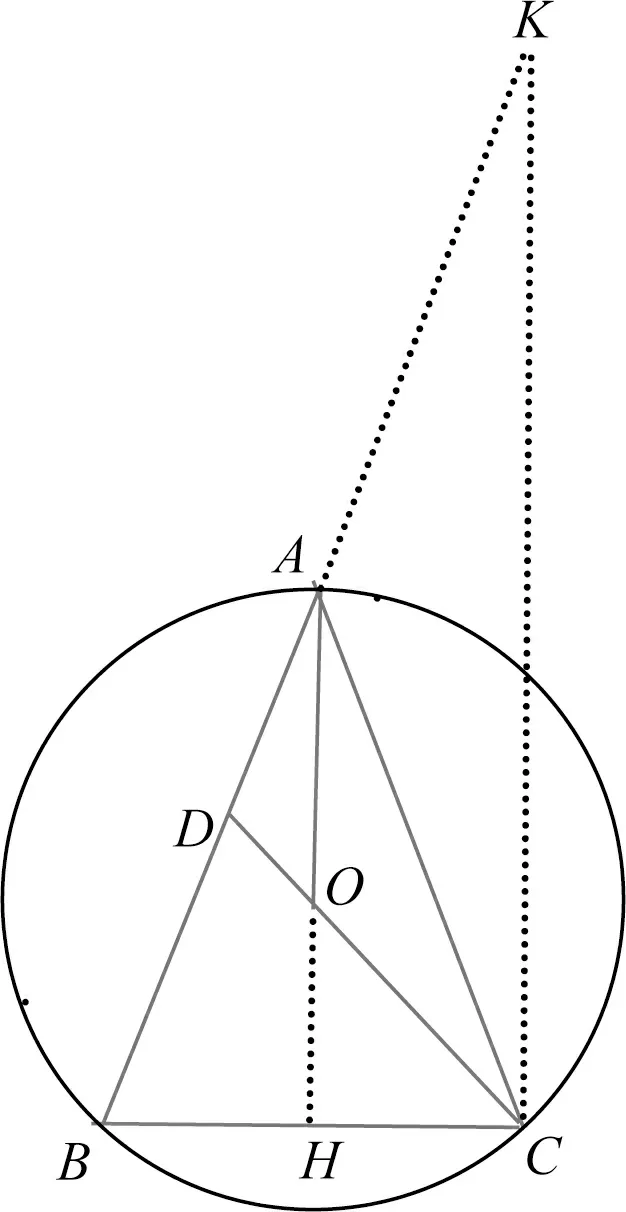
图13

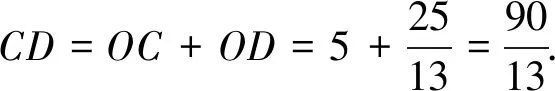
解法12如图13，作CK∥AH交BA延长线于点K，因为AH∥CK，所以△ABH∽△KBC，

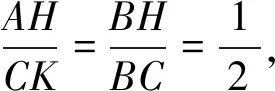
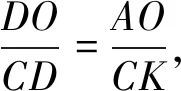
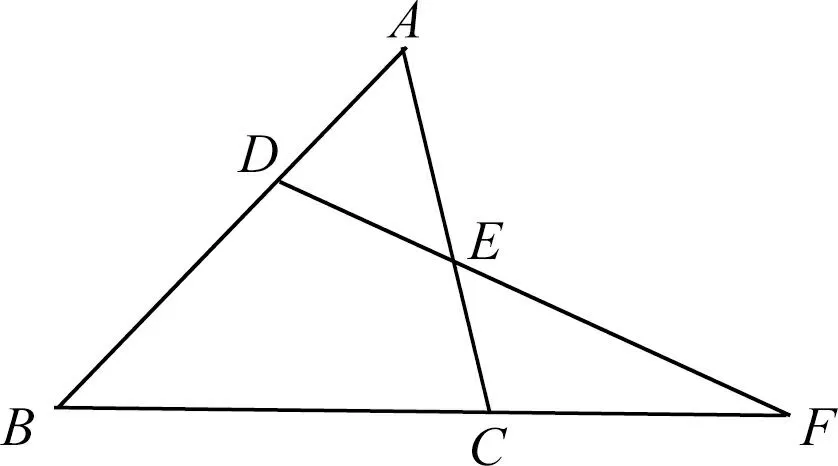
图14

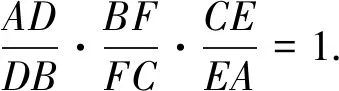
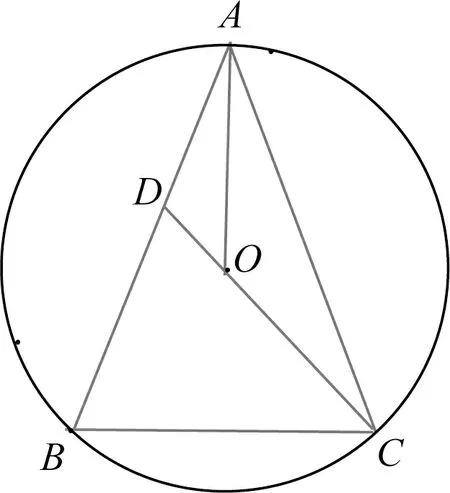
图15

解法13如图15，由(1)知∠DAO=∠OAC，

因为OA=OC，所以∠OAC=∠OCA，

所以∠DAO=∠OCA，又∠ADO=∠CDA，

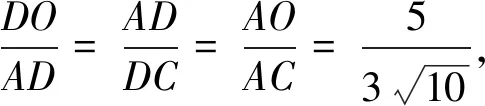
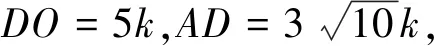
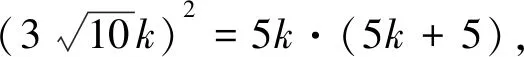
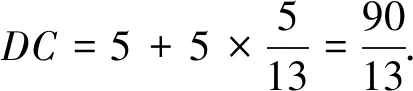
评注此解法依托第(1)问的中介作用，揭示了命题中的条件与隐含条件，为寻求解题途径指明了方向，无需添加辅助线，使解决问题的方法简单流畅、别具一格，达到了化繁为简、化难为易的目的，而且还可以开拓学生的思维，对学生学习兴趣的培养也大有裨益．

中考试题都是经过命题专家在课标、教材的指引下精心设计的，只有深入其中去思考、去体会、去研究，才会发现其引导功能和教学价值．在日常教学中，教师若能选取类似本文提到的这样的试题，留给学生足够的思考时间，提供给学生展示自己想法的机会，并组织学生对不同思路进行适当的比较和讨论，学生就能自然地把题目涉及到的基本图形的相关性质等相关知识加以联系，构建成一个整体，达到灵活应用数学知识的程度．