城市轨道交通连续梁和简支梁的结构噪声特性比较

韩江龙, 吴定俊, 李 奇

(1.太原理工大学 土木工程系，太原 030024；2.同济大学 桥梁工程系，上海 200092)

不少文献研究了桥梁结构噪声的计算方法、噪声特性和降噪措施，如Li等[1-3]、刘林芽等[4-5]、罗文俊等[6]、Wu等[7]、石广田等[8]，但均以单跨简支梁为主。Kimura等[9]研究指出：板边梁的固定支承能够增加输入阻抗，减小噪声辐射。张博[10]研究了两端固定支承与简支支承的单跨箱梁的结构声辐射后，提出了“短接刚性梁法”(见图1)，通过增加梁的整体刚度来降低总体A权级噪声，并试用于上海轨道交通一号线北延伸二标段和明珠线浦东段。该法实质是通过增加约束把简支梁变成连续梁以增加结构的整体刚度，减小振动。然而，Au等[11]的结论是板的刚度越大，结构的振动频率越大，移动荷载产生的声压也越大。高飞等通过计算分析指出：选择合适刚度的桥梁支座能够改善连续梁桥的动力响应，但对结构辐射噪声的影响很小[12]。虽然文献[10]和文献[12]有本质上区别的，但都对结构的整体刚度有影响。以上文献的结论并不一致，因此有必要研究相同跨数的简支梁和连续梁的声辐射，同时注意邻跨的影响。文献[13-16]分别在简支梁的噪声研究中提到了邻跨或多跨的共同作用。

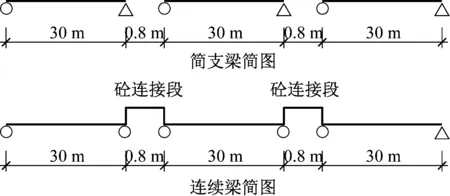
图1 短接刚性梁

本文以单线槽型梁为例，比较三跨简支梁和三跨连续梁的声学性能优劣。以车-轨-桥的相互作用理论为基础，忽略声压对桥梁动力响应的影响，对梁体进行动力分析；并将获得的动力响应作为声场边界条件，借助SYSNOIS软件用模态叠加法分析梁体结构的声辐射。而后比较不同类型梁的声学特性，为工程结构选型提供参考。详细的模态叠加法计算理论、过程及试验验证参考笔者所在团队的文献[17-18]，本文仅简单介绍。

1 结构振动与声场分析

1.1 车辆-轨道-桥梁相互作用分析方法

采用有限元方法分别建立车辆子系统和桥梁/轨道子系统运动微分方程，用模态叠加法分别对两个子系统解耦。

解耦的车辆子系统和桥梁/轨道子系统运动微分方程分别为

(1)

(2)

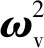
两个子系统之间通过轮轨滚动接触理论来联系。第j个车轮的轮轨法向力由赫兹非线性弹性接触理论确定

(3)

式中：Gj为赫兹接触常数;Δwrj为轮轨法向压缩量，直接由轨道不平顺、车轮位移、轨道位移决定，也间接反映了列车车速对轮轨激振力大小及频率的影响。

用分离迭代法或分离同步法求解子系统的响应。

1.2 轨道短波不平顺

根据ISO 3095:2005标准生成短波不平顺的空间样本。当列车速度为40～80 km/h时，不平顺波长取0.052～1.2 m(>0.63 m的波长由标准公式线性外推)，不平顺的频率值为9～400 Hz，能满足结构噪声的频率为20～300 Hz的要求。

1.3 车辆模型

本文考虑6节C型地铁车辆编组情况。车桥耦合振动计算中车辆模型的计算参数见文献[18]。实测60列列车速度约在70 km/h波动，故计算车速设定为70 km/h。

1.4 声场求解

声压小幅波动时，满足Helmholtz方程和Sommerfeld辐射条件的波动方程是线性的，用直接边界元法可以在频域内建立结构表面法向振速v(ω)与场点声压p(ω)的线性关系。通过模态叠加法可以得到结构的模态坐标向量与表面法向振速v(ω)的关系，进而获得场点声压p(ω)与结构的模态坐标向量的关系，如下式[19]

p(ω)=MATV(ω)TC

(4)

式中：MATV(ω)T=jωA(ω)TBΦ，是模态声传递向量，与结构的几何形状、场点位置、计算频率、声介质和结构振型有关。A(ω)T为声传递向量;ω为声源激励频率;B为投影矩阵，仅与结构的几何形状有关；Φ为结构振型组成的矩阵;C为结构模态坐标组成的向量，由结构振动分析求解得到。

借助SYSNOIS在频域内求解场点模态声传递向量MATV(ω)。耦合动力分析得到时域内离散的桥梁模态坐标C(ti)，对模态坐标C(ti)进行离散Fourior变换，得到频率为ω时的C(ωi)，利用已经求得的MATV(ω)在ω处插值获得MATV(ωi)。然后由式(4)求得频域内离散形式的场点声压，最后进行Fourior逆变换可得到离散的声压时程响应p(ti)。

2 结构几何尺寸与场点布置

2.1 结构几何尺寸

简支槽型梁标准跨径30 m，计算跨径28.8 m，底板厚0.24 m，梁端1.2 m范围内底板加厚为0.32 m。混凝土强度等级C50。由于梁端振动很小，其几何尺寸对噪声特性的影响不大，故仅示出跨中截面的几何尺寸，如图2所示。为便于比较，保持跨数和梁高不变，将三跨简支槽型梁变为连续梁，取消图1的短接段，见图3。

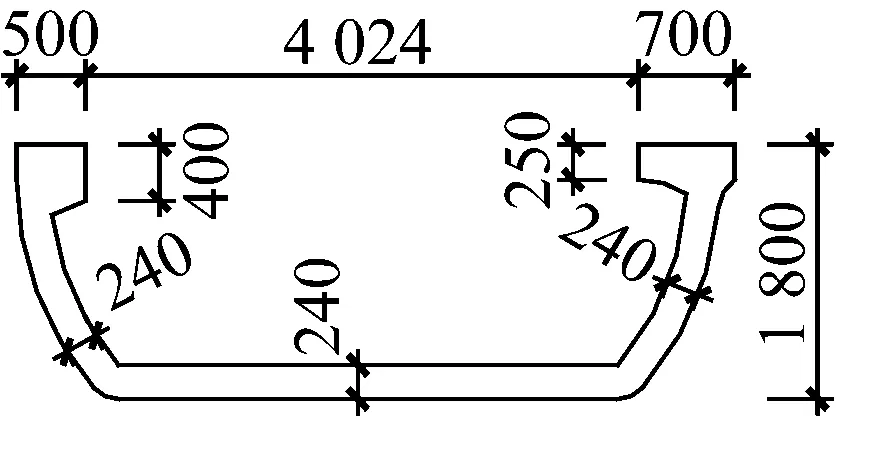
图2 梁截面(mm)

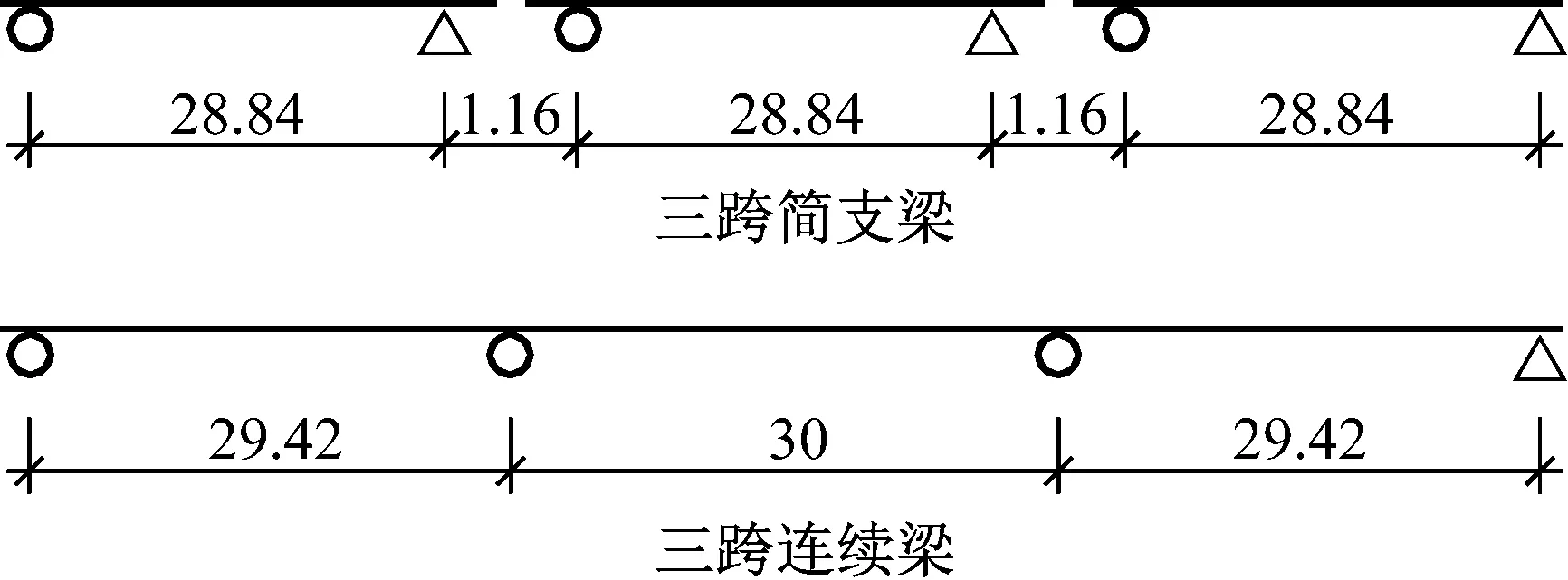
图3 三跨简支梁与连续梁简图(m)

2.2 声压场点布置

在梁的跨中(连续梁中跨跨中)截面布置声场点，从轨道的中心线开始，布置在距轨道中心线30 m的范围内(见图4)。

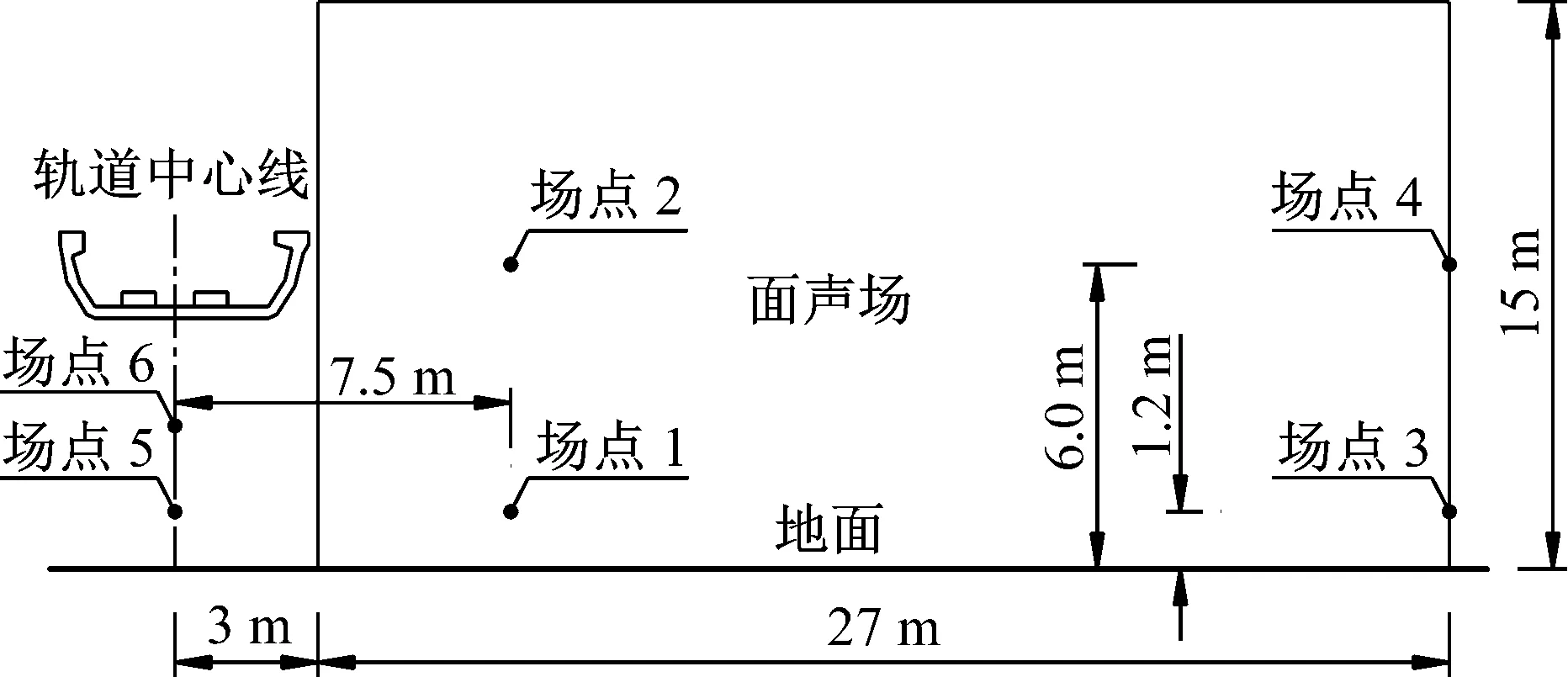
图4 场点布置

3 MATV(ω)激励频率的计算步长

计算MATV(ωi)时，声场的计算频率范围为20～200 Hz。三跨梁规模大，计算步长的大小直接影响MATV(ωi)的插值精度和计算时间。

频域内点声源的声场表达式如下

(5)

式中：Q为点声源的强度;r为场点到点声源的距离。

式(5)为周期函数;r为参数;ω为自变量;则函数的周期为T=2π×c0/r。r越大，周期越小,数值计算时，ω需要的计算步长越小。同理，桥梁结构噪声也含有类似的关于ω和r的复指函数，为了保证数值计算的精度，计算步长的确定应以远场点的计算为依据。《铁路边界噪声限值及其测量方法》(GB 12525—1990)规定了距轨道中心线30 m处的噪声限值，故以此处场点来确定MATV(ωi)的计算步长。槽型梁试算结果见表1，表中18 m、21 m、30 m为计算场点到轨道中心线的水平距离。

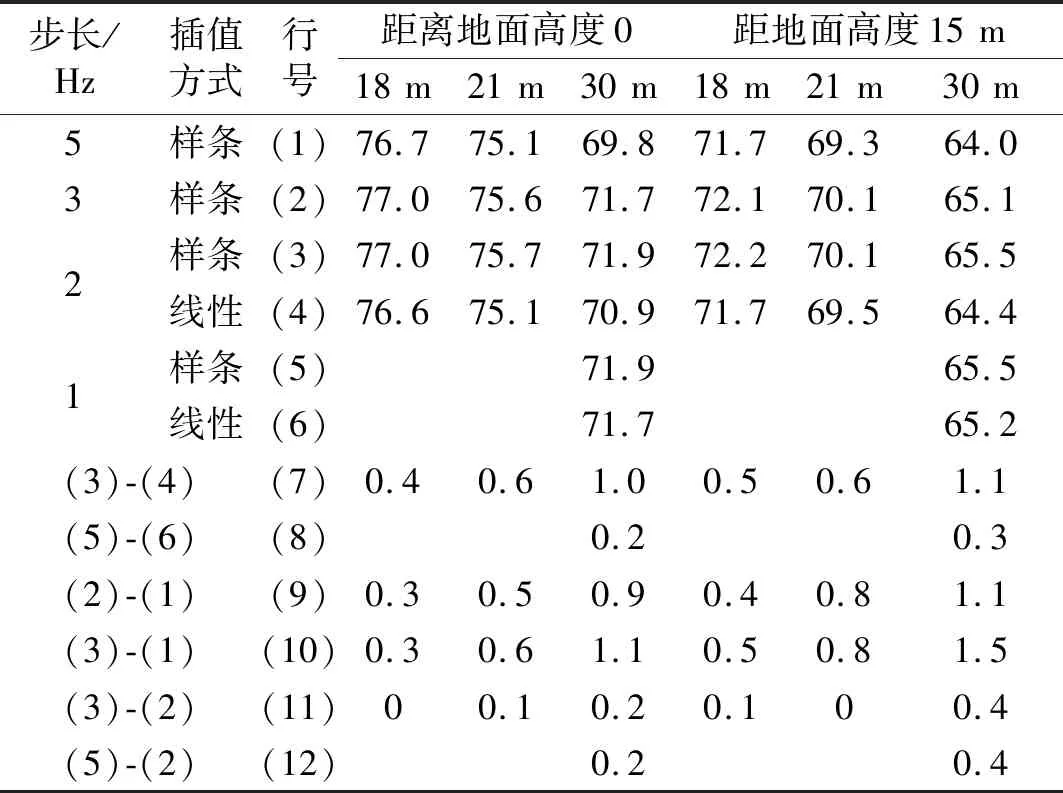
表1 不同计算步长的线性声压级比较

声压级的测试精度为1 dB。表1中第(1)～(5)行显示:随着步长减小，声压级计算结果趋于稳定。第(9)、(10)行显示：距轨道中心线不超过18 m时，步长5 Hz、3 Hz和2 Hz的计算结果最多相差0.5 dB，三者具有相同的计算精度。第(10)～(12)行显示：当r=30 m时，5 Hz的步长计算结果误差超过1 dB，而步长由3 Hz减小到2 Hz和1 Hz，声压级的变化值小于0.5 dB，采用样条插值计算，步长3 Hz、2 Hz和1 Hz具有相同的计算精度。而第(7)和第(8)行显示步长为2 Hz和1 Hz时，线性插值和样条插值的结果已很接近，选用2 Hz的步长，线性插值计算也能满足计算精度的要求。

图5显示：步长5 Hz计算的MATV(ωi)与其它三个步长计算的MATV(ωi)形状相似，计算频率在60 Hz以下四种步长的计算结果一致，曲线接近重合。计算频率大于60 Hz后，步长5 Hz与其它三个步长的计算结果差别较大，在100～140 Hz之间差约50%。而步长1 Hz、2 Hz和3 Hz计算的MATV(ωi)在20～200 Hz的整个频率段上几乎一致，改变步长对计算精度的提高已不明显，与表1结论相同。

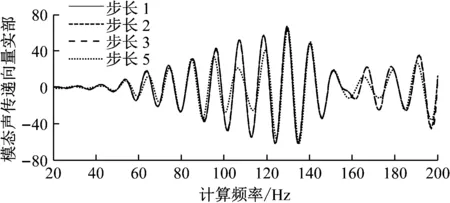
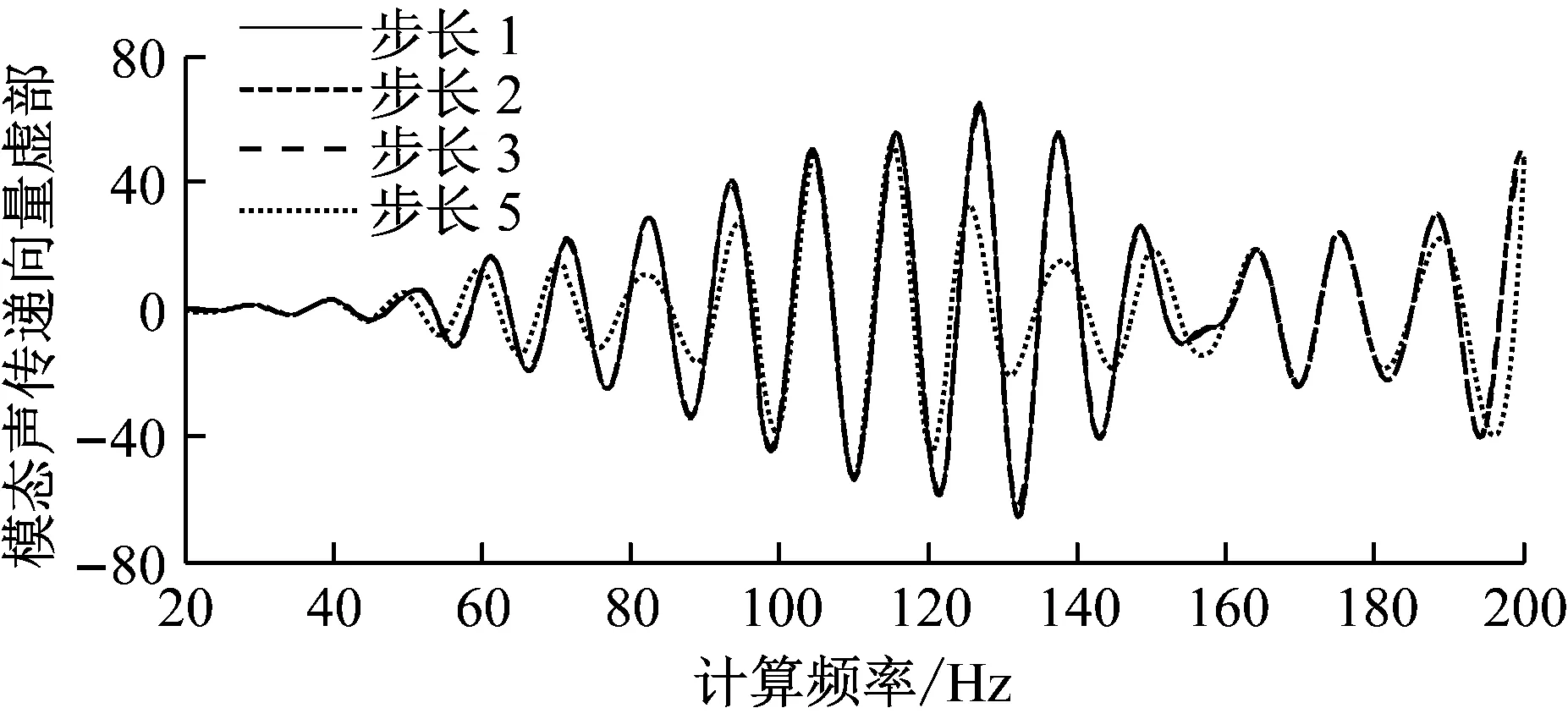
图5 某远场点MATV(ωi)计算比较(Pa)

边界元法的求解矩阵为非对称的满秩矩阵，且结构规模大，求解耗时长，占用空间大。步长由3 Hz变为2 Hz，计算时间比原来增加了50%，考虑计算精度和耗时，选用3 Hz的步长计算MATV(ωi)，即20 Hz,23 Hz,26 Hz,…,200 Hz;后处理编程时采用样条插值计算。

4 结构振型的影响

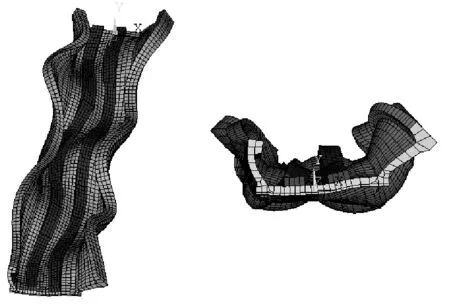
声压级谱1/3倍频程中心频率控制到200 Hz，为了保持频率计算的完整，桥梁结构的振型频率应大于中心频率200 Hz的上限频率223.9 Hz，简支梁考虑到128阶模态，连续梁的模态阶数更高，达350阶以上。梁典型振型如图6所示。

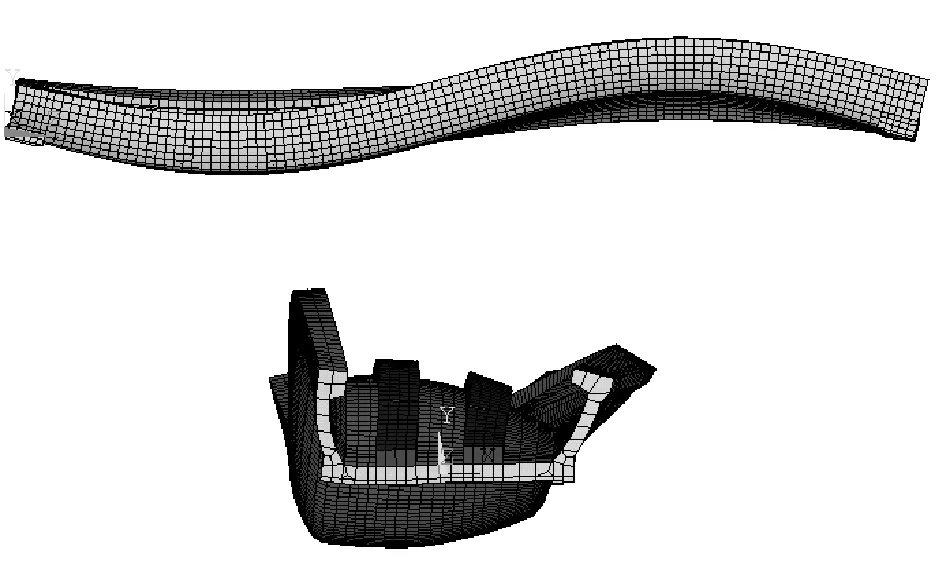
(a) 简支梁第4阶

(b) 简支梁第34阶

(c) 连续梁第17阶

(d) 连续梁第18阶

(e) 连续梁第19阶

图6 梁振型图

Fig.6 Girder vibration modes

5 计算方法试验验证

本文关注结构低频噪声。轮轨噪声的低频成分不大，经过槽型梁衍射和透射，在结构噪声峰值频率范围内的削弱相当可观，其对结构噪声的干扰可以忽略。在上海某轨道交通槽型梁下进行结构噪声试验。采用LMS SCADASⅢSC305W数据采集系统，采样频率12 800 Hz；丹麦G.R.A.S.公司电容式麦克风布置在梁底跨中竖平面内。实测和计算值的频谱吻合很好。

6 声压特性

6.1 邻跨的影响

表2显示：无论是连续梁还是简支梁，对近场点1、2和5，中跨振动引起的声压级接近或等于总声压级，二者相差不超过0.5 dB；边跨引起的声压级远小于总声压级，可以忽略边跨影响。对于远场点3和4，边跨和中跨引起的声压级相近，二者对总声压的贡献相当。

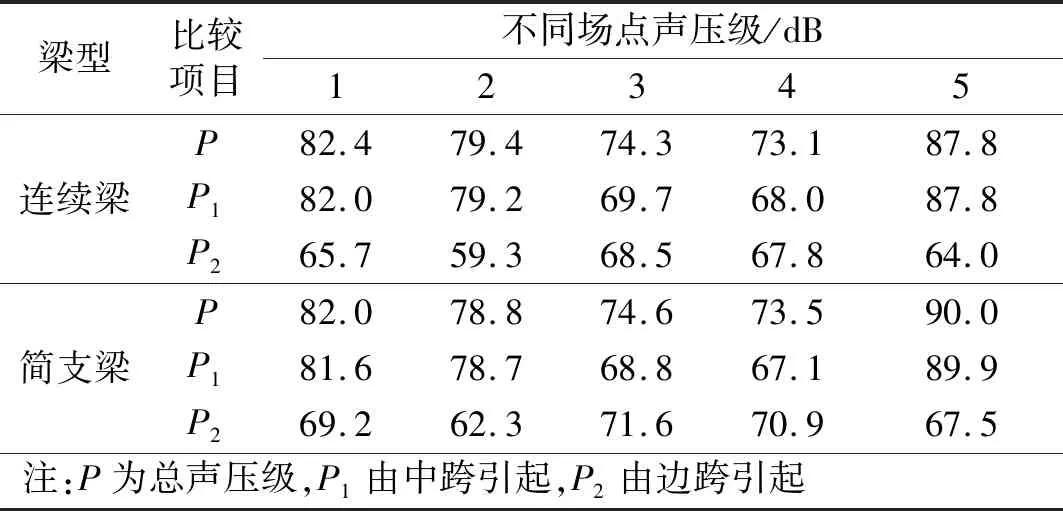
表2 不同场点线性声压级

从图7可知,边跨对场点声压的影响随着到轨道中心线距离的增加而增强。距轨道中心线7.5 m以内，边跨振动产生的声压远小于中跨产生的声压，可以忽略边跨的影响。当到轨道中心的距离增加到30 m时，边跨产生的声压与中跨产生的相当。因此比较简支梁和连续梁的声学性能时，远场点的声压须考虑边跨的影响。

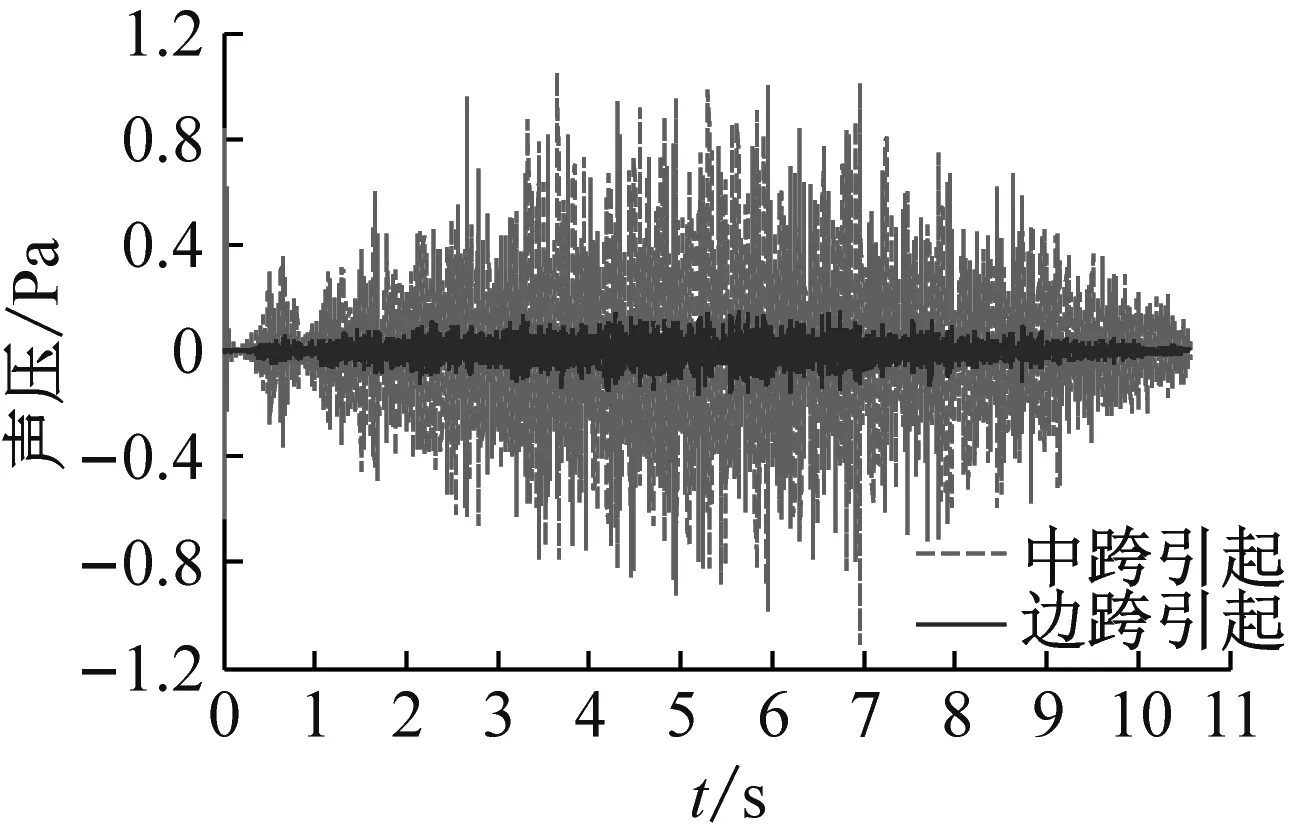
(a) 场点1

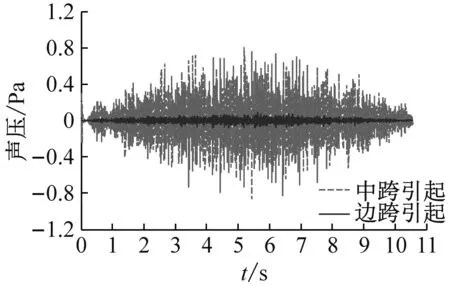
(b) 场点2

(c) 场点3

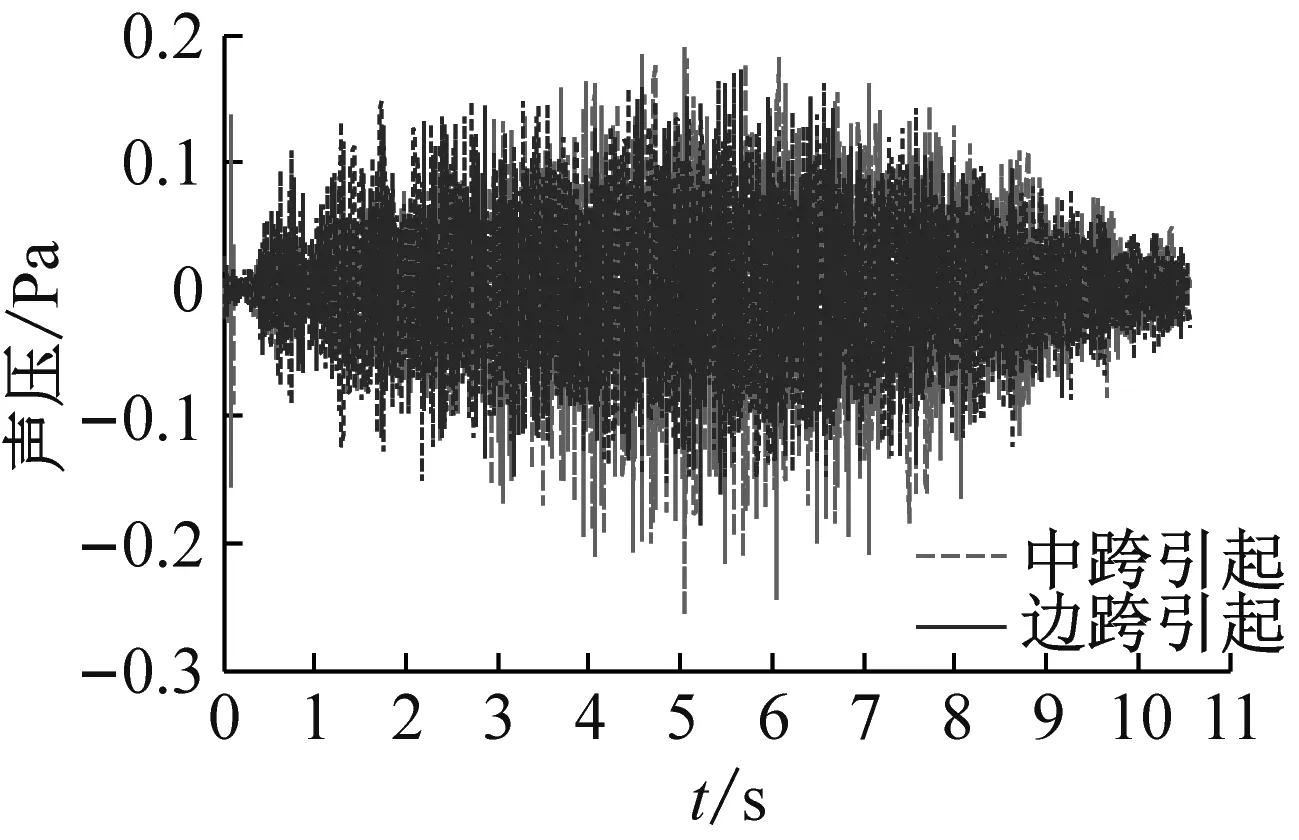
(d) 场点4

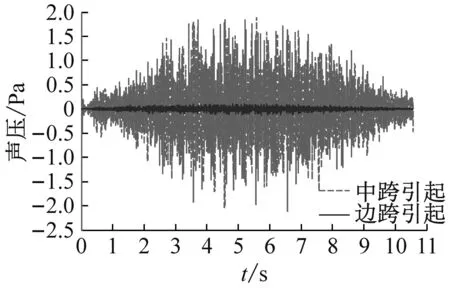
(e) 场点5

图7 连续梁场点声压时程

Fig.7 Sound pressure time history from the continous girder

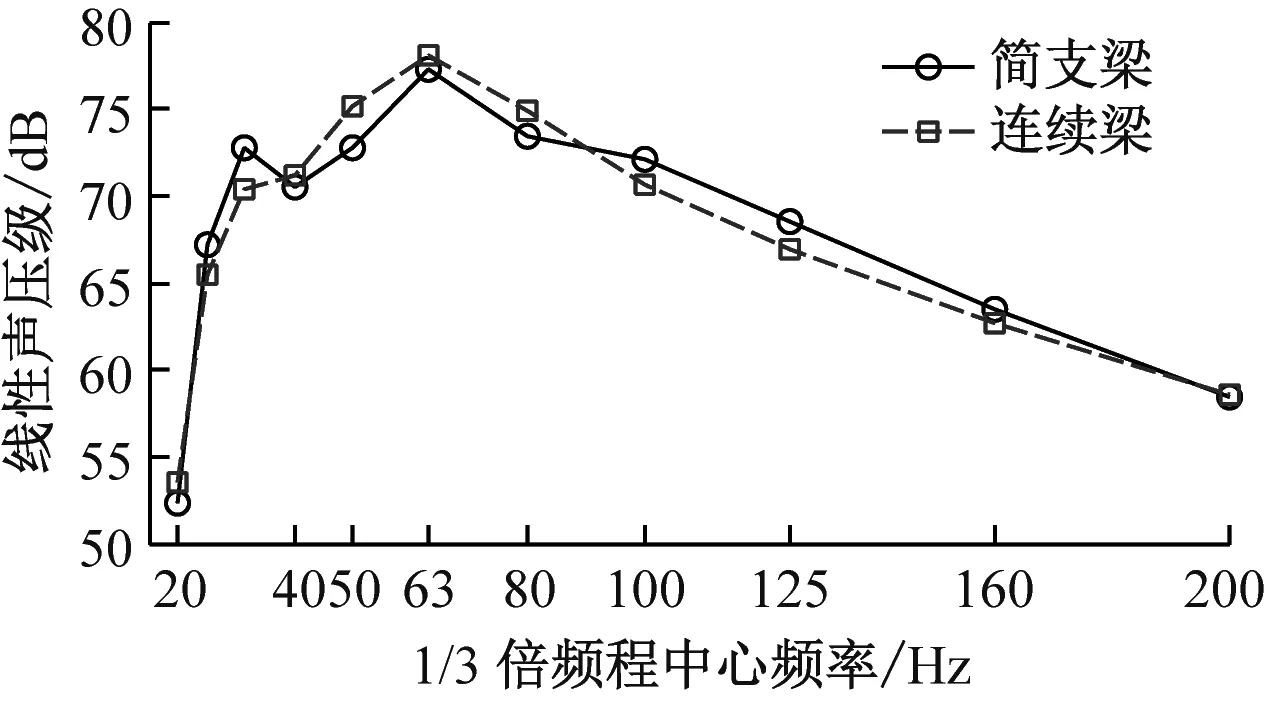
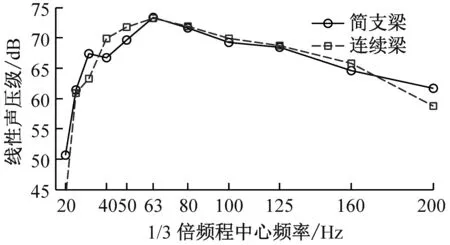
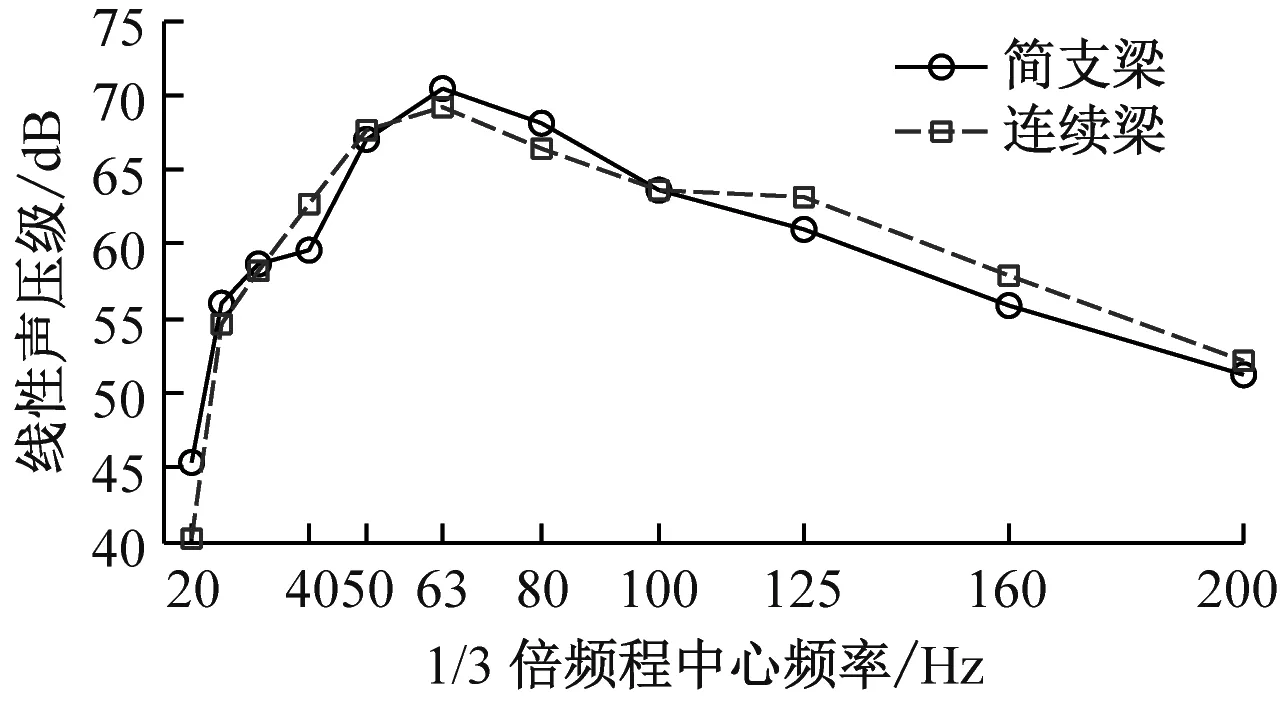
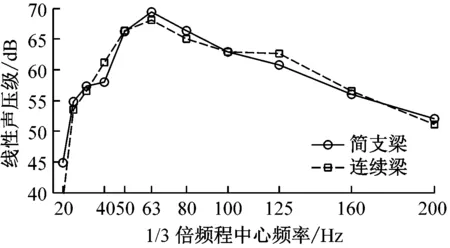
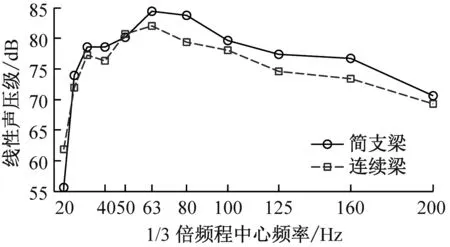
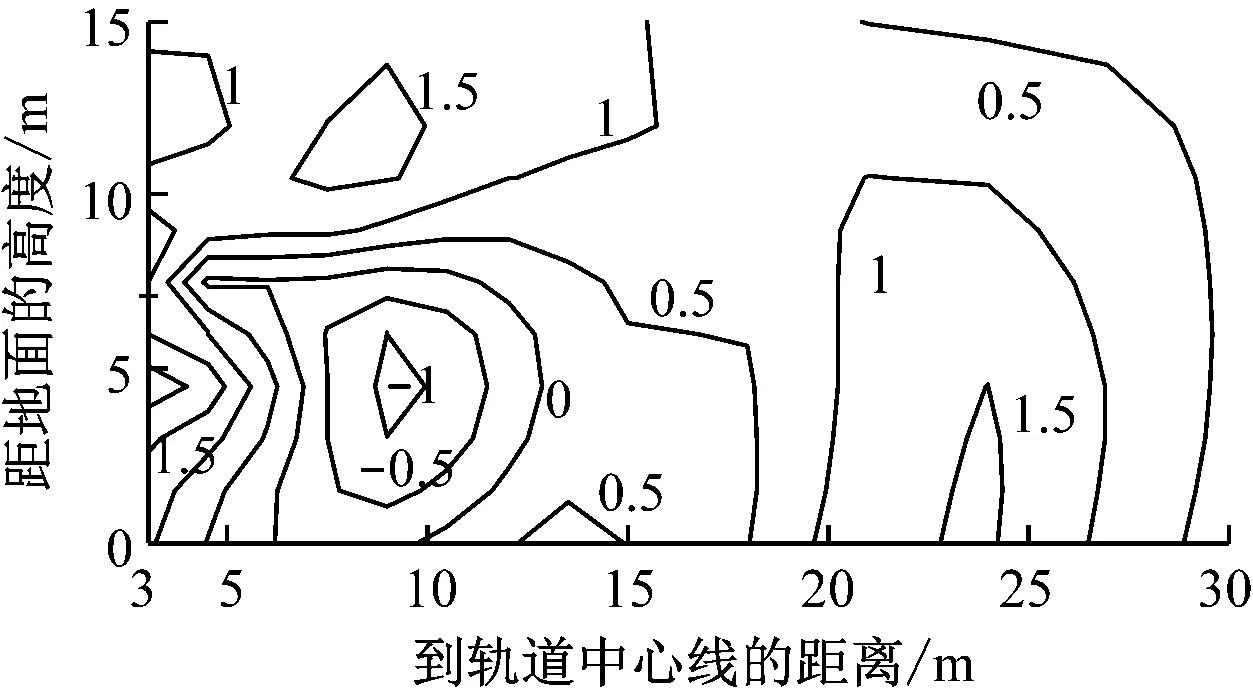
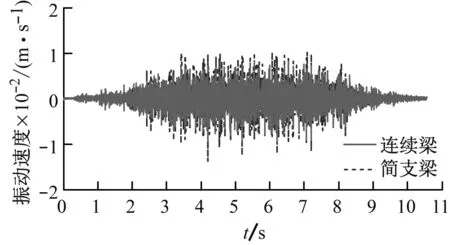
产生这种现象的原因可用图8解释。每跨梁在相同位置处的点声源点1和2传播到场点的距离分别为L1和L2，h为场点垂直于桥梁轴线方向的距离。h越小，L1/L2越大，当h=30 m时，1.4

6.2 降噪效果

表2中除桥下场点5噪声水平改善较大外，连续梁和简支梁其余场点的总声压级相差不明显。图9显示声压级谱也相似，声压能量集中在40～125 Hz，峰值频率在63 Hz左右；连续梁对桥下场点5在63～100 Hz区段能降低2～4 dB，其他场点正常运营速度下几乎没有改善。图10的空间声场绝大部分场点的声压级改变量小于1 dB，距轨道中心30 m的距离上，各场点的声压级几乎没有变化。因此连续梁的声学性能并不比简支梁优越，尤其是对于中远场而言，通过简支梁变连续梁来降低结构噪声难以收到预期的效果。

图8 三跨梁声传播示意图

(a) 场点1

(b) 场点2

(c) 场点3

(d) 场点4

(e) 场点5

图9 不同场点的1/3倍频程声压级谱

Fig.9 1/3 Octave sound pressure level pectrum

图10 连续梁面声场声压级减小量/dB

Fig.10 Reduced sound pressure level of the continous girder sound field

由于约束增加，连续梁的整体刚度增大，受低频模态控制的结构竖向位移明显小于简支梁(见图11)；但对产生可听噪声的底板竖向振动速度(已滤去小于20 Hz的成分)而言，简支梁与连续梁差别不大(见图12)，

图11 三跨梁的中跨跨中竖向位移时程

由于声压级是对数计算，这种轻微的减小对总声压级的影响不大。截面局部变形、振动是产生可听结构噪声的主要原因，且槽型梁的底板对噪声贡献大，增强梁的边界约束只能改善梁的整体刚度而对底板的弯曲刚度无甚改善，故而只能降低低频竖向位移，而对20 Hz以上能产生噪声辐射的振动改善效果不大。

图12 中跨底板跨中竖向速度时程

7 结 论

(1) 研究结构噪声时，远场点声压需要计入邻跨的影响。

(2) 与总长和跨径相同的简支梁相比，相同截面的连续梁结构噪声无明显改善。

(3) 连续梁不能有效降噪的原因在于增加约束改变的是结构整体刚度而不是梁截面板的弯曲刚度。