基于多模型模糊扩展卡尔曼滤波的电池SOC预测

王 勇，陈万顺

(芜湖职业技术学院信息工程学院，安徽芜湖 241006)

随着人们对节能、环保的重视，电动汽车在生活中的使用越来越普遍。电池生产与使用是电动汽车的核心技术之一。对电池的荷电状态(State of Charge，SOC)的精确测量直接影响对动力电池的保护和能量的利用效率，具有重要意义[1]。然而动力电池的SOC与电池充放电次数、环境温度、充放电速率之间存在复杂的非线性关系，难以实时精确测量。

传统的开路电压法测量精度较高，但是测量过程中为了等待电池内部恢复平衡需要较长的静置时间，难以在实际应用中实时测量。安时积分法结构简单，运用广泛，但在测量过程中误差会积累，测量精度不高。以神经网络为代表的智能测量方法，具备很强的非线性拟合能力且抗干扰性能好。但此类方法需要大量数据事先训练，且硬件实现复杂，难以推广[2-3]。较为成功的方法是卡尔曼滤波方法，了解被测对象的系统噪声和观测噪声的统计特性之后，可以实现最小方差估计。该方法计算量小，尤其适合微处理器硬件实现[4-5]。但是卡尔曼滤波过程中对数学模型的精度要求较高，电池的老化会造成其内部参数的变化，从而限制了卡尔曼滤波预测电池SOC的精度。针对电池寿命周期中不同阶段的充放电特性有所变化，本文设计了一种多模型扩展卡尔曼滤波方法，以期提高对电池SOC的测量精度。

图1 一阶戴维宁模型

1 电池模型的建立

为了降低测量系统的运算量，本文采用一阶戴维宁模型描述电池的充放电特性，如图1所示。R1为电池内部的欧姆电阻，电阻R2和电容C并联描述电池充放电过程中的极化现象[6]。E(t)为电池内部的电动势，E(t)与电池的SOC值s(t)之间存在非线性关系：E(t)=F(s(t))。U(t)为电池的端电压。

选取电池的SOC值s(t)和极化电容C两端的电压UC(t)为状态变量，以充电电流I作为输入量，电池的端电压U(t)作为观测量，建立电池的状态空间表达式。以T为采样周期进行离散化可得[7]：

(1)

U(k)=F(s(k))-R1I(k)-UC(k)+v(k).

(2)

其中，Q0为电池的容量，w(k)为系统过程噪声，其方差为Q(k)；v(k)为观测噪声，其方差为R(k)。

2 扩展卡尔曼滤波

由于状态变量s(k)与观测量U(k)之间存在非线性关系，本文采用扩展卡尔曼滤波对数学模型进行一阶线性化处理，估计电池核电状态s(k)，式(1)(2)所示系统的形式如式(3)(4)所示。

x(k+1)=Ax(k)+Bu(k)+w(k).

(3)

y(k+1)=F(x(k))+v(k).

(4)

运用扩展卡尔曼滤波的计算过程如下：

①初始化系统状态x(0)、y(0)与协方差矩阵P0；

④对式(4)进行一阶线性化，获得观测矩阵H(k)=∂F/∂x；

在扩展卡尔曼滤波过程中对观测方程中的非线性函数F(x(k))展开成泰勒级数，并忽略其二阶以上的项，实现线性化。当采样时间足够短，滤波误差较小时，则可以使用扩展卡尔曼滤波。

3 模糊多模型扩展卡尔曼滤波算法

一般锂电池循环充放电500次以上，电池的容量仍能保持在标称容量的80%以上。但电池充放电次数的增加，电池的充放电特性会发生变化。本文分别选取电池循环充放电0次、300次和500次时对其进行参数辨识，建立其数学模型。为了降低模型精度造成的误差，本文采用多个数学模型描述电池充放电的特性，并针对各个数学模型分别进行卡尔曼滤波。如图2所示，取实际观测量U(k)和所建立的第i个电池模型之差的范数αi(k)=‖U(k)-yi(k)‖表征当前模型与实际电池的符合程度。αi(k)的值越小，说明当前模型越精确。以αi(k)为输入，以第i个电池数学模型所占权重θi(k)为输出，建立模糊推理系统。αi(k)的论域是[0,1]，θi(k)的论域也为[0,1]。选取模糊集合{S、MS、M、MB、B}描述αi(k)和θi(k)，其中，S代表小，MS代表中等偏小，M代表中等，MB代表中等偏大，B代表大。采用高斯型函数描述αi(k)和θi(k)的隶属度。在模糊推理系统中存在以下逻辑关系：

ifαi(k) is S，thenθi(k) is B；

ifαi(k) is MS，thenθi(k) is MB；

ifαi(k) is M，thenθi(k) is M；

ifαi(k) is MB，thenθi(k) is MS；

ifαi(k) is B，thenθi(k) is S。

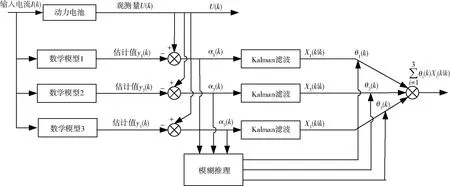
图2 模糊多模型卡尔曼滤波原理图

4 仿真实验

为了验证算法的有效性，本文选取常用的容量为2800 mAh的18650电池为测试对象。基于MATLAB软件搭建仿真模型如图3所示，根据式(1)(2)，以充放电电流为输入I(k)，以电池的端电压U(k)为观测量建立电池的状态空间方程。观测过程中受到均值为0、方差为0.0006的高斯噪声的干扰。针对使用寿命周期中不同阶段的电池进行参数辨识，获取其欧姆电阻R1、极化电阻R2以及极化电容C的值。构建数学模型进行卡尔曼滤波，并针对各模型的对观测值的估计，通过模糊推理，得出该模型状态估计的权重。在测试过程中，电池的初始SOC值为0.75，以2.8 A的电流充电50 s，然后以2.8 A的电流持续放电100 s，期间每1 s采样1次。

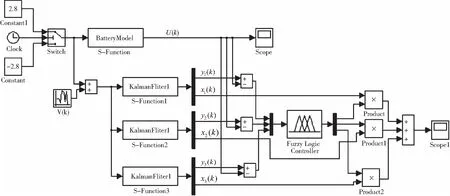
图3 仿真模型

以仿真模型中电池模型BatteryModel中的状态变量值作为理想值，分别采用传统的卡尔曼滤波和多模型模糊卡尔曼滤波进行状态估计，预测电池SOC的值。预测结果如图4和图5所示。

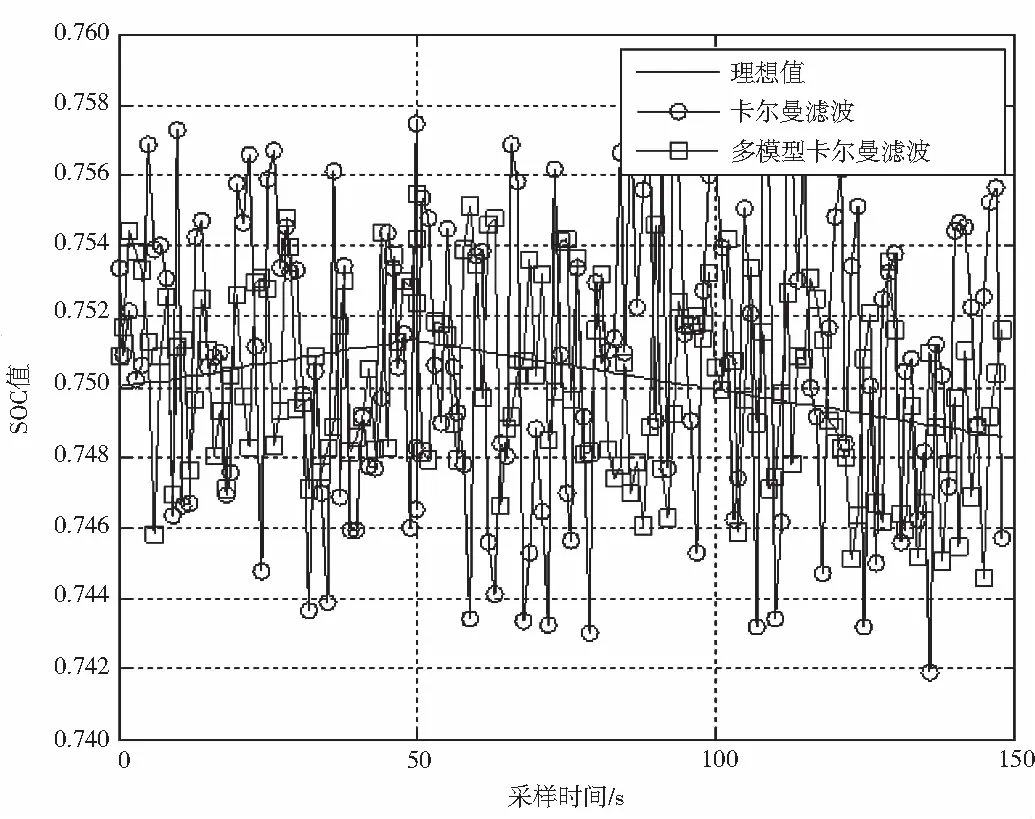
图4 预测结果对比

图5 预测结果误差分析

通过预测结果可以发现，多模型模糊卡尔曼滤波的预测结果更接近理想值，其与理想值的绝对误差更小，这说明多模型模糊卡尔曼滤波算法具有一定的应用价值。

5 结语

在对电池SOC值预测的过程中，卡尔曼滤波计算量小，易于计算机硬件实现，被广泛使用。多模型模糊卡尔曼滤波算法是在传统卡尔曼滤波的基础上，分别建立多个数学模型描述不同使用阶段电池的充放电特性，并采用模糊推理综合各模型预测的结果。该方法在不增加硬件成本的前提下，提高了实时预测的精度，具有一定的工程应用价值。