空间复用MIMO系统的信号检测方法比较

张明军

(阜阳职业技术学院，安徽阜阳 236031)

1 研究背景

MIMO技术是无线通信领域的重大突破，作为一种通信技术，其最先是由Marconi(1908)采用多天线系统来解决无线通信中衰落问题所引出的。Telatar(1995)在对MIMO系统的信道容量进行平坦衰落分析发现，天线数目的增加会使信道容量呈现线性增长，这一发现使得MIMO技术飞速发展。Bell实验室的研究学者(1996)提出了空间信号处理的系统框架，为MIMO技术全面推向无线通信领域奠定了基础。随着电子通信应用的普及，各国科研机构对MIMO技术不断改良，使MIMO技术成为移动通信领域中的关键技术，发展前景巨大。MIMO技术通过增益极大提升了信道容量以及信道传输性能。并且MIMO技术实现了多路信号的并行传输，提高了系统的频谱效率，但与此同时，发射信号的重叠和码间干扰给接收端的信号检测增加了难度[1]。因此，有效检测接收端的信号成为空间复用MIMO系统中的一项具有挑战性的任务，系统的检测方法性能的优劣直接对MIMO系统的整体性能造成影响。对此需要探寻一种低复杂度与高性能相统一的信号检测算法来提升MIMO系统的性能。

常见的系统信号检测方法可以分为线性和OSIC两大类，在对高性能系统信号检测方法的研究上，郁光辉[2]针对信道复用输入的重叠干扰问题提出一种分层调制的球形检测算法，相较于MSD算法而言，其在误码率以及复杂度性能上分别得到5%和20%的提升。李小文[3]在V-BLAST算法的基础上进行改进与优化，并与其它几种常见信号检测算法进行实验比较分析，结果显示提出的优化算法在性能上得到明显增强。赵新雪[4]提出了一种通过缩小ML向量检索的双向最大似然检测算法，通过实验仿真可知，与传统最大似然检测算法相比较此算法性能有所提高。本文在构建系统模型的基础上对4种信号检测方法进行仿真实验比较，从而择优选择检测算法。

2 空间复用MIMO系统及模型

MIMO系统是依靠多根天线来实现信号的接收与发送的，发射天线与接收天线数量多少决定了MIMO系统的发送速率以及信号接收质量的高低。所有的数据均是处在同一频带在同一时间发送的，这也使得MIMO系统频谱利用率非常高。常提到的MIMO信道指的是在发射端与接收端之间的无线信道。该系统的典型结构如图1所示。

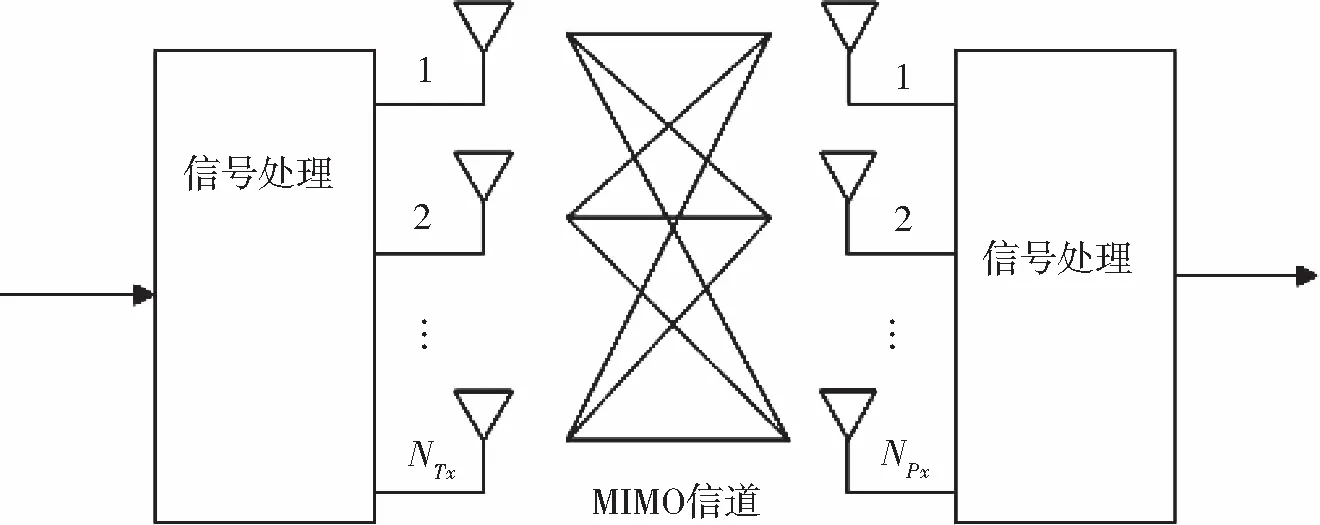
图1 MIMO系统信道模型

对于具有NRx×NTx的MIMO系统，其MIMO信道矩阵H可以确定为NRx×NTx。发射符号向量x由NT个独立符号构成，接收向量y可以表示成：

(1)

其中，Ex为发射信号的能量，z=[z1,z2,…,zNRx]T是噪声向量[5]。在该系统中，每一个接收天线均接收来自NTx根发射天线的信号，其接收到的是空间和频带上均相互重叠的多路信号。

对于某种空时编码的MIMO系统，信号的传输速率一定不超过信道容量，假设传输速率为：

R(SNR)=kC(SNR)=k×min(NRx,NTx)×log(1+SNR),0≤k≤1.

(2)

将MIMO系统能够得到的传输速率与SISO系统的最大传输速率log(1+SNR)的比值定义为空间复用增益，即:

r=R(SNR)/log(1+SNR)
=k×min(NRx,NTx)×log(1+SNR)/log(1+SNR)
=k×min(NRx,NTx).

(3)

那么，MIMO系统能够获得的最大空间复用增益为rmax=min(NRx,NTx)。其中，NTx为发射天线数量，NRx为接收天线数量。

图2为NRx×NTx的空间复用MIMO系统，它的发射天线和接收天线数分别为NTx和NRx。

图2 空间复用MIMO系统

y=Hx+z.

(4)

其中，H指的是信道矩阵，矩阵中的hij元素代表的是第i根发射与第j根接收天线的增益，j=1,2,…,NRx，i=1,2,…,NTx。令矩阵H中的第i个列向量用hi表示，则空间复用MIMO系统的公式可以进行变形，如(5)所示：

y=h1x1+h2x2+…+hNTxxNTx+z.

(5)

MIMO系统接收到的信号是叠加信号，除了会接收到发射信号外，还往往存在噪声信号，如何有效地对接收信号分离来排除噪声信号的干扰是信号检测技术最关键的问题。本次信号检测基于前文所构建的V-BLAST系统模型来完成。

3 空间复用MIMO系统的信号检测方法

3.1 线性信号检测

在系统的接收端，每根天线都同时接收来自NTx根发射天线的信号，致使在接收端所有信号混叠在一起。为了从混叠信号中检测出来自目标发射天线的期望信号，必须最小化或消除来自其他天线的干扰。

线性信号检测方法的原理是通过矩阵W(加权矩阵)来对信道进行逆转，从而实现期望信息与干扰信号的分离，如式(6)所示，可以有效地实现对每个信号的检测。

(6)

下面就对常用的线性信号检测方法中的ZF与MMSE检测方法进行简要的介绍。

3.1.1 ZF信号检测

ZF信号检测方法在接收端强制将信号间干扰置为零，使用如式(7)所示的加权矩阵进行干扰消除：

WZF=(HHH)-1HH.

(7)

其中，(·)H表示艾米特转置操作。将伪逆矩阵WZF与接收信号向量y相乘，实现了信道的逆转：

(8)

(9)

利用酉矩阵Q，因为其满足‖Qx‖2=xHQHQx=xHx=‖x‖2，所以噪声功率的期望值为：

(10)

ZF信号检测的优点是简单实用，但也因为其检测方法完全消除了符号间干扰，同时通过与伪逆矩阵WZF相乘将高斯噪声放大，因此ZF算法的抗噪声性能很差。

3.1.2 MMSE信号检测

(11)

其中，加权矩阵的第i个行向量wi,MMSE由最优化方程得出：

(12)

使用MMSE加权矩阵可以得到以下关系：

(13)

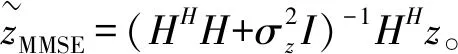
(14)

由于

(15)

式(15)的噪声功率可表示为：

(16)

根据酉矩阵算法的特征，进行相乘时并不会使向量的范数发生变化，也就是‖Vx‖2=‖x‖2，噪声功率的期望值为：

(17)

对于线性滤波进行信号检测来说，最小的奇异值越小，则会导致噪声增强所造成的影响更为突出，以上两种线性检测方法分别所造成的噪声增强影响如式(18)(19)所示：

综上现状分析不难发现，学校教育亟需基于人工智能，展开教学系统重构的系统性研究，实现信息技术与学科教学线上线下资源、教学、管理等系统的深度融合，创新动态开放的课程构成和教学模式，改变教学机制与学习范式，进而构建智能化、精准化、个性化的教育新常态，使“人工智能+”教育变革落到实处。鉴于此，本文拟通过辨析认知人工智能的功能效用，对“人工智能+”对教育变革的影响、变革理念与实现路径展开深入探讨，以推动“人工智能+教育”的发展，提高学校教育实效性。

(18)

(19)

3.2 OSIC信号检测

线性检测方法的复杂度比较低，其检测性能不如非线性检测方法。在这样的情况下，为实现检测方法的低复杂度与高性能，可以采用OSIC方法来进行优化与改善，在并不大改变复杂度的前提下提高检测性能。该方法是通过对已检测数信号数据在接收端进行删除，使得后面的检测信号受到干扰减小。

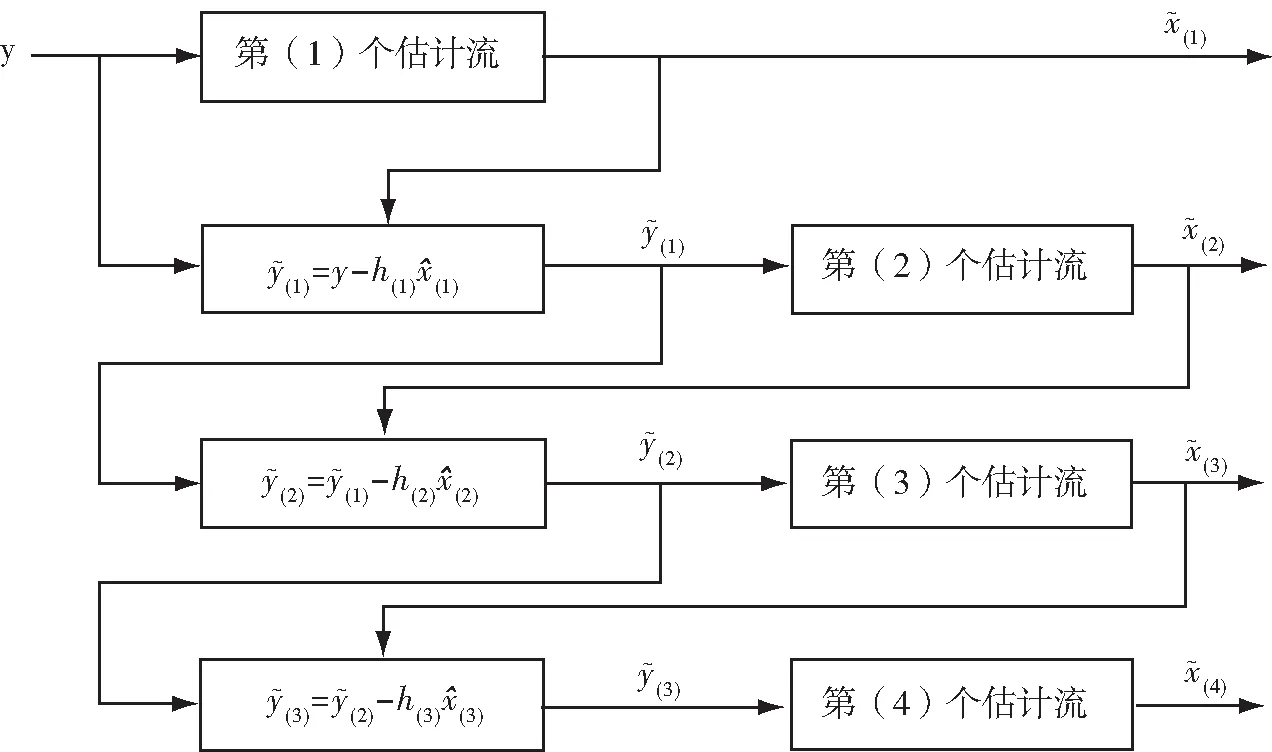
图3 用于4个空间数据流的OSIC信号检测示意图

(20)

3.2.1 基于MMSE准则的OSIC检测

基于MMSE准则的OSIC检测方法记为MMSE-OSIC检测方法，检测时需要对最大SINR信号进行检测。原本的MMSE检测方法获得的SINR信号为：

(21)

其中，Ex表示的是发送信号能量，wi,MMSE和hi分别代表加权矩阵的i个行向量与信道矩阵H的i个列向量。从前面的MMSE检测方法可以知道SINR最大化的同时，均方差维持在最小的范围内，这样可以根据加权矩阵来获得NTx个SINR，从而判断最大的SINR信号所处的层。后续对第二个信号进行检测时已经对第一个信号所产生的干扰进行了消除。如果假定第一个被检测出的信号记为(1)=l，那么对第一个符号所产生的增益向量删除后，信道矩阵则可变形为：

H(1)=[h1h2…hl-1hl+1…hNTx].

(22)

3.2.2 基于ZF准则的OSIC检测

(23)

由于采用了优化排序的操作，OSIC信号检测方法能在一定程度上得到分集增益从而提升检测性能，然而其优化排序的操作会造成计算的复杂度有所增加。在OSIC信号检测方法中，所有符号的分集阶数都大于NRx-NTx+1。由于排序的原因，第一个检测符号的分集阶数也大于NRx-NTx+1，前面符号检测的正确性直接影响剩余符号的分集阶数。OSIC检测方法在性能和复杂度之间取了合理的折中，其基本思想已经成为MIMO信号检测领域的一个研究热点，受到了广泛的关注。

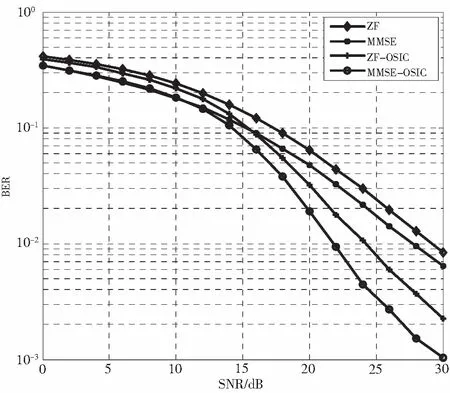
图4 4×4天线配置下4种检测方法的性能比较示意图

4 各检测方法仿真及性能比较

为了对不同检测算法的性能进行比较，在相同天线配置的情况下进行仿真。图4给出了ZF、MMSE、ZF-OSIC、MMSE-OSIC这4种信号检测方法的误码率随信噪比变化的情况。可以看出，在信噪比相同的情况下，MMSE-OSIC检测方法的误码率要低于ZF-OSIC检测方法，其次是MMSE检测方法，最后是ZF检测方法。这说明，在同一个MIMO信道模型中，OSIC信号检测方法性能最优，MMSE次之，最差是ZF检测方法。造成这一结果的原因在于OSIC信号检测方法通过事先优化排序以及删除信号等方式对干扰进行了消除，使得检测性能较线性检测方法呈现大幅度提高。MMSE-OSIC检测性能优于ZF-OSIC检测方法，是由于其在进行SINR排序的同时还考虑了噪声所带来的影响，故而较仅单纯进行SNR排序的ZF-OSIC检测方法的检测性能更优。而MMSE算法利用使均方误差最小的特征降低了ZF算法噪声的影响，所以其检测性能也要优于ZF检测方法。

5 结论

本文对4种空间复用MIMO系统的信号检测方法进行了简要介绍，并运用MATLAB进行仿真比较。比较结果显示，ZF、MMSE、ZF-OSIC和MMSE-OSIC这4种检测方法，性能最好的是MMSE-OSIC信号检测方法，其次是ZF-OSIC方法，排在第三位的是MMSE信号检测，ZF的检测性能最差。