企业光伏系统容量的优化配置

郝思鹏，张前，杨李星

(1.南京工程学院 电力工程学院，江苏 南京 211167； 2.南通市供电公司，江苏 南通 226001)

近年来随着光伏产业的迅猛发展，分布式光伏推广与应用已成为一种趋势[1]。企业光伏系统是分布式光伏的重要体现方式之一，针对我国工商业用电量较大、成本相对较高的问题，合理配置光伏系统容量成为有效降低企业运营成本的关键。

企业光伏系统的安装大多根据场地面积及负荷大小配置容量。根据发改能源〔2018〕823号文关于优化光伏发电新增建设规模、降低补贴强度的通知以及拉大分时电价差的政策，合理规划光伏建设容量和降低用能成本是企业光伏投资者的必然选择。诸多学者对光伏容量配置进行了研究，文献[2]分析了分布式光伏发电并网的成本收益,比较了不同容量和运营模式下分布式光伏并网的经济效益。文献[3]研究了光伏发电预测曲线和分时电价特性。文献[4]根据光伏出力与负荷时序特性，以光伏消纳率为目标函数确定光伏建设规模。文献[5]对不同电价场景下上网电价规制类型对主体收益造成的影响进行了分析。文献[6]利用峰谷分时电价引导用户改变用电方式，提升负荷与光伏的相关性从而提高光伏的置信容量。文献[7-9]建立了分布式风光电源规划模型，但没有考虑电源衰减率的影响。

整体而言，上述文献从不同角度建立光伏容量规划模型，但未综合考虑光伏、负荷及峰谷分时电价的时序特性对容量配置的影响，忽略了四季光伏出力与负荷用电差异，且容量配置方法较复杂。本文提出光伏发电效率、光伏出力、负荷曲线与峰谷分时电价时序特性、峰平电价差等是影响容量配置的关键因素，在此基础上建立了以用能成本最低为目标的全寿命周期企业光伏容量配置的优化模型，且利用实例证明容量配置方法的合理性。

1 企业光伏容量配置的关键因素

1.1 光伏出力时序特性及发电效率

地域、季节是影响光伏发电的重要因素。从地域上讲，一般纬度低、少雨地区太阳辐射较强，如西藏地区太阳辐射能极为丰富；而从季节上看，光伏夏季出力最强，冬季最弱，春秋两季相近，且春夏日照持续时间长于秋冬，以冬季条件配置的光伏容量在夏季不能得到良好的消纳。因此，光伏出力须考虑地域和季节因素。

1.2 负荷用电时序特性

企业负荷时序特性由产业结构决定。工业负荷依其上班制度白天呈现单峰或双峰变化趋势[10-11]，且与光伏出力特性类似，同时工业负荷时序特性也表现出一定的季节特征，如图1所示，四季中负荷特性变化的一般规律为：夏季偏高，冬季偏低，春秋两季处于中间位置。而商业负荷四季用电特性差异不大，时序特性曲线基本一致，夏季负荷持续时间较其他季节稍长。

图1 工业负荷四季时序特性曲线Fig.1 Seasonal time-sequence characteristic curves of industrial load

1.3 峰谷分时电价下的最优光伏容量及收益分析

光伏系统收益来源于光伏自发自用节省的电量电费、上网售电费用及用电补贴。根据国家光伏发电补贴政策，本文不考虑补贴所带来的收益，因此光伏通过峰谷分时电价节省的电量电费在收益中占主要部分。峰谷分时电价由地方政府制定，如图2所示：00:00—08:00、08:00—12:00及17:00—20:00、12:00—17:00及20:00—24:00分别为南京地区低、高、平电价时段[12]，双峰曲线表示负荷Pd，单峰曲线表示光伏出力Ppv，其中光伏出力大于负荷的面积为剩余光伏上网售电部分。若继续加大光伏建设容量，光伏出力将覆盖更多负荷，节省更多电量电费；但若节省的电量电费合计售电收益不一定能抵消光伏容量增加导致的成本增加，则光伏建设容量必存在最优值。

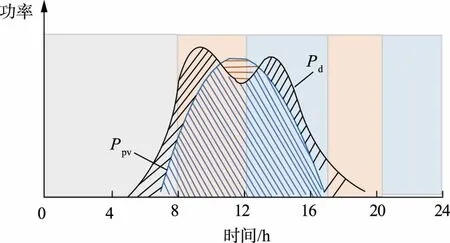
图2 分时电价下光伏-负荷简化分布图Fig.2 Simplified distribution of PV-load under TOU price

理想收益是指不同电价时段负荷尽可能消纳光伏出力，尤其是高电价时段。光伏出力良好且负荷用电量较大、持续时间越久，收益就越大，可抵消更多投资、运维成本。而最高负荷与光伏出力峰值通常不会同时出现在高峰电价，因此系统收益与三者的时序特性密切相关。光伏出力与负荷存在波动性和不确定性，故提出依据分时电价负荷划分方案简化计算系统的收益。

负荷处于低谷电价时段系统收益

(1)

负荷处于平段电价时段系统收益

(2)

负荷处于高峰电价时段系统收益

(3)

系统日收益

(4)

式(1)—(4)中：lprice、fprice及hprice分别为低、平、高电价；ee为光伏上网电价；p、q为日分时电价时段；T为系统运行时段总天数；Δt为时间变化量。

2 光伏系统容量优化配置

2.1 负荷归算

本文采用加权平均法进行负荷归算[13]。将负荷月用电量作为年度典型负荷曲线中该日的权值，对年度负荷数据进行加权平均得到典型负荷曲线。首先统计第i年第j月第k天的用电量Qi,j,k及第i年总用电量Qi,即：

(5)

(6)

式(5)—(6)中：Pi,j,k,t为第i年第j月第k天第t时刻(以小时算)负荷功率；N为每月的总天数。基于加权平均法得到的负荷第i年t时刻典型负荷数据为

(7)

2.2 光伏折算

本文采用直接预测法对光伏出力进行折算，根据各地光伏出力效率不同，提出功率变换系数及四季等效天数的概念，分别作为评判光伏出力强度与时长的指标。功率变换系数随太阳光入射角及周围温度变化而变化，光伏四季出力等效天数Rs根据当地历史气象数据简单折算，而且光伏日最大发电功率与容量呈比例关系，一天中各时刻光伏出力与最大发电功率也存在函数关系。考虑光伏电池衰减率后的光伏功率可表示为[14]：

Ppv=Pimax×Pspv*.

(8)

Pimax=as×η×Qpv×(1-d)i.

(9)

Pspv*=p1t2+p2t+t0.

(10)

式(8)—(10)中：Pimax光伏系统在第i年s季节日最大发电功率；as为当地各季节功率变化系数，s=1,2,3,4分别为春、夏、秋、冬季；η为光伏电池转换效率；Qpv为光伏装机容量；d为光伏电池衰减率；Pspv*为各季节日光伏出力标幺值[15]；p1、p2为拟合曲线系数；t0为时刻变量初始值。

为简化工程计算量，将折算后的负荷、光伏以小时为单位取均值，对二者曲线进行阶梯化处理，使连续数据离散化，以梯形图代替折线图，可提高系统的可操作性和计算速度。若要提高系统的精度可相应地缩短时间间隔，使结果更加精确。如图3所示。

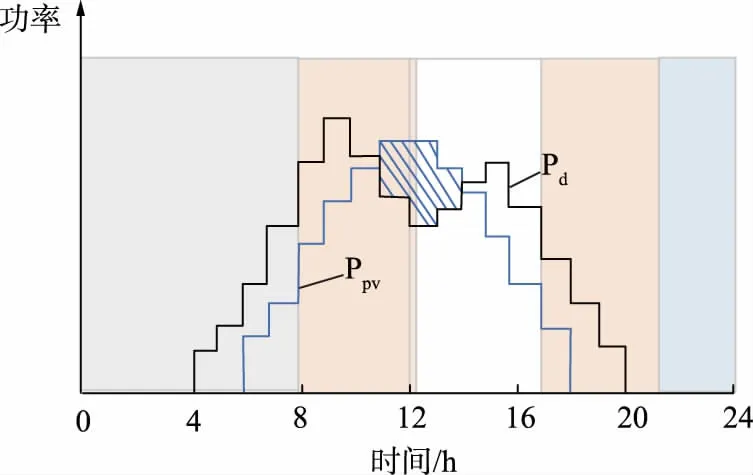
图3 分时电价下光伏-负荷梯形图Fig.3 PV-load ladder diagram under TOU price

2.3 优化模型

用能成本是指企业投资光伏系统的总成本与收益的差值，单位用能成本为用能成本与负荷用电量的比值。全寿命周期用能成本为系统全寿命周期总成本与效益之差，二者均与光伏系统的容量密切相关。本文以全寿命周期用能成本最低为目标建立函数，即

minF=Cpv-Y.

(11)

式中Cpv、Y分别为全寿命周期光伏系统总成本与收益。系统收益由自发自用节省的电量电费和与电网交互费用决定，由式(4)简化收益计算法及光伏四季等效天数可得出全寿命周期系统收益为：

(12)

(13)

式(12)—(13)中：Yi为第i年系统收益；n为全寿命周期年限；ir为通货膨胀率；dr为贴现率。

光伏系统运行期内总成本包括建设成本和运行维护成本，建设成本包括光伏板、逆变器等设备成本及安装费用[16-17]。全寿命周期光伏系统总成本为：

(14)

Ccap=QpvIpv.

(15)

式(14)—(15)中：Ccap为光伏初期建设成本；Cw为光伏系统年运行维护成本，可按建设成本的1%～3%计算[18]；Ipv为光伏单位容量装机成本。

2.4 具体流程

光伏系统容量优化配置是个多元素的时序性问题。本文分别对负荷、光伏进行了简化处理，结合分时电价负荷划分的收益计算法及光伏系统建设成本建立了容量优化配置模型，可得企业光伏容量优化配置流程如图4所示。

图4 企业光伏系统容量优化配置流程Fig.4 Optimization configuration flowchart of enterprise PV system capacity

3 实例分析

以2018年江苏南京地区工业I、II及商业负荷为例进行分析，图5为工业I、II负荷简化后的曲线。其他参数有：ir=0.015，dr=0.09，ee=0.36 元/kWh，Ipv=6 元/W，寿命周期为20 a。

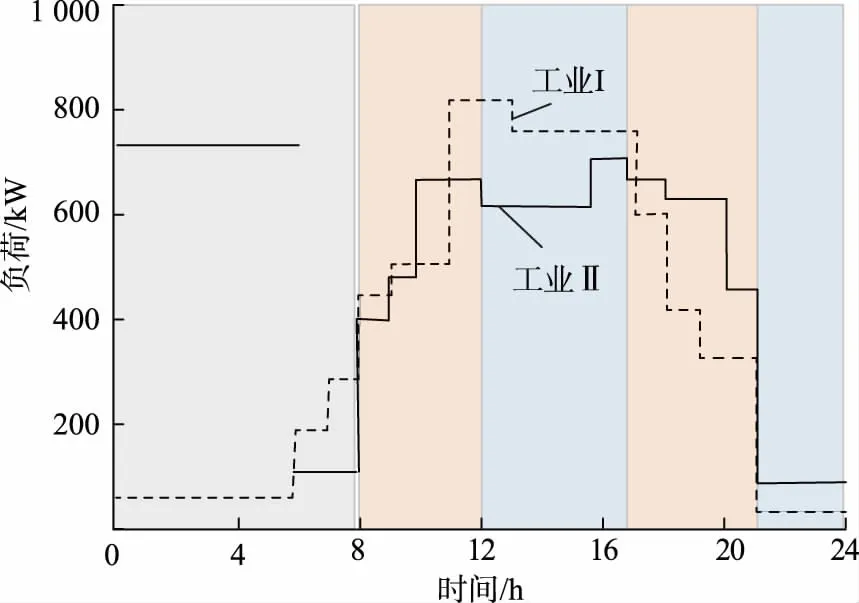
图5 分时电价下工业负荷日用电简化曲线Fig.5 Simplified curves of daily electricity consumption of industrial load under TOU price

江苏地区工业负荷分时电价为：峰时电价为1.044 7 元/kWh，平时电价为0.626 8 元/kWh，谷时电价为0.308 9 元/kWh;对应的商业负荷分时电价分别为：1.378 2 元/kWh、0.859 5 元/kWh、0.365 8 元/kWh；西藏地区采用单一电价，即工业负荷电价为0.663 1 元/kWh，商业负荷电价为0.852 1 元/kWh。以南京为例，光伏出力采用历史数据回归拟合函数，即：

(16)

式中P1pv*、P2pv*、P3pv*、P4pv*分别为春、夏、秋、冬季光伏出力(标幺值)。

将工业Ⅰ、商业负荷于南京、拉萨地区分别配置光伏容量，结果见表1。

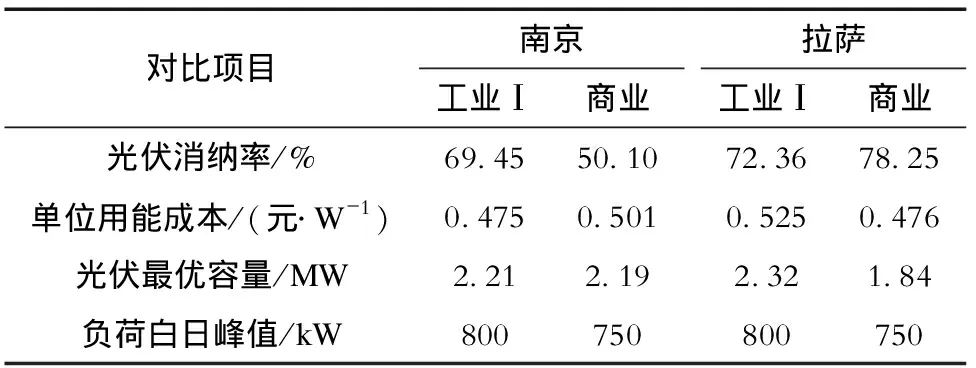
表1 不同地区负荷配置结果对比Tab.1 Comparison of load configuration results of different regions

从表1可以看出：拉萨地区商业光伏最优容量低于江苏，这是由于拉萨地区光伏发电效率较高，且其日照时间长达12 h，尤其是每天持续到晚上8时，与商业负荷用电特性吻合度很高。拉萨工业负荷最优容量略高于江苏可能与其采用较低的单一电价有关。由此可知，光伏发电效率是容量配置的重要因素之一。

将工业Ⅰ、Ⅱ负荷于南京地区分别配置光伏容量,结果如图6所示。从图6可以看出：随光伏容量的增大，用能成本呈先减后增的趋势，光伏容量开始增大时，各电价下光伏出力覆盖负荷的面积逐渐增大，此时系统收益增长速度大于光伏成本增长速度,故用能成本呈下降趋势；当光伏容量达到某值后,受限于光伏上网电价和成本，用能成本转呈上升趋势。

表2为南京地区不同负荷配置结果对比。

从表2可以看出：工业Ⅰ容量较工业Ⅱ容量大是因高峰电价时段，光伏消纳率占有相当优势，单位用能成本高是因容量大光伏成本高造成的。实例说明了即使负荷总用电量相同，而在各电价下负荷用电量不同的情况下，光伏消纳率和配置容量都不同。高电价时段下光伏消纳率较高时，可适当增加光伏配置容量。因此，综合考虑光伏出力、负荷曲线与峰谷分时电价三者的时序特性是容量配置关键因素之一。此外，由工业Ⅰ与商业负荷配置结果可知，相似光伏安装容量下，商业负荷用电量小而最优容量高是因其分时电价高，因此分时电价对容量配置也至关重要。

图6 工业光伏容量-用能成本变化曲线Fig.6 Variation curves of industrial PV capacity- energy consumption cost

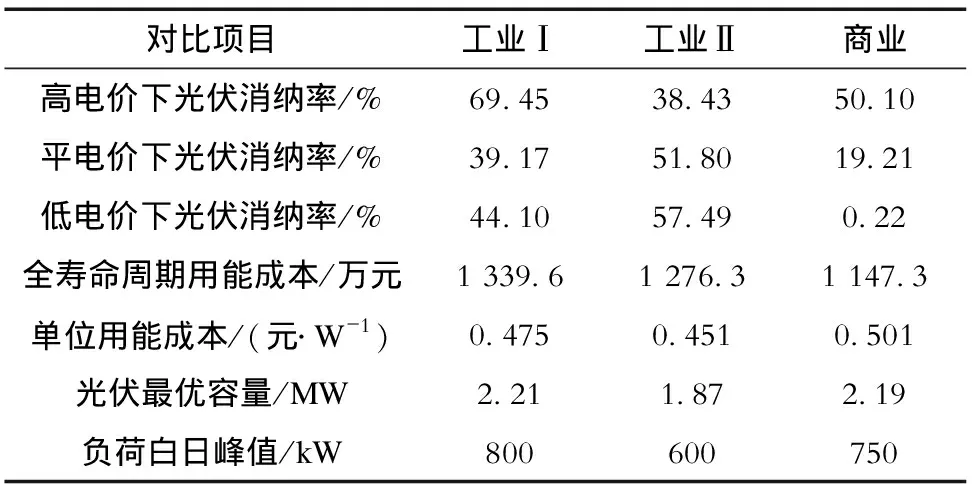
ⅠⅡ/%69.4538.4350.10/%39.1751.8019.21/%44.1057.490.22/1 339.61 276.31 147.3/(·W-1)0.4750.4510.501/MW2.211.872.19/kW800600750

考虑光伏出力主要在峰、平电价时段，以工业Ⅰ为例，改变峰平电价差，不考虑用户侧响应，结果如图7所示。从图7可以看出：当高峰电价提高0.1 元/kWh，平段电价减少0.1 元/kWh，即峰平电价差为0.2 元/kWh时，光伏容量增加7.11%，单位用能成本下降2.1%；当高峰电价提高0.2 元/kWh，平段电价减少0.2 元/kWh，即峰平电价差为0.4 元/kWh时，光伏容量增加8.21%，单位用能成本下降3.2%；当高峰电价提高0.4 元/kWh，平段电价减少0.4 元/kWh，即峰平电价差为0.8 元/kWh时，光伏容量增加9.52%，单位用能成本下降3.8%。可见，随着峰平电价差的增大，光伏最优容量增加，用能成本减低，但下降速度逐渐减缓。因此峰平电价差的拉大可增大光伏最优配置容量，并降低系统用能成本。

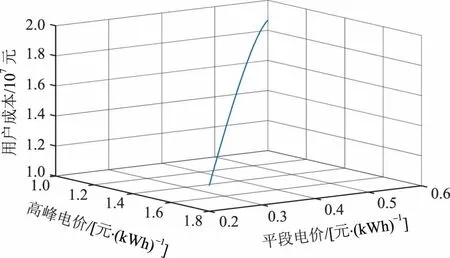
图7 分时电价差与用能成本变化曲线Fig.7 Variation curves of TOU price differences and energy consumption cost

综上所述，本文提出的光伏容量配置方法能够综合不同地区的企业负荷、峰谷分时电价、光伏出力情况进行配置，实现经济性最优，并且在三者时序相关性较高的情况下，可增加光伏配置容量。相同地区的工商业因采用的峰谷分时电价不同，安装光伏系统的适宜程度也不同，如南京地区工业较商业更适宜安装光伏系统，而拉萨地区反之。最后，随着峰平电价差的拉大，也可促进光伏配置容量的上升，故通过调节峰谷分时电价可推广企业光伏系统的运用。

4 结束语

本文建立了以企业用能成本最低为目标的全寿命周期光伏容量配置模型。基于此模型的仿真结果表明：光伏出力、负荷曲线以及峰谷分时电价三者的时序特性直接影响光伏系统的容量配置；峰平电价差也是光伏容量配置的重要影响因素；继续增加电价差或推出扶持光伏行业的政策，可有效降低企业投资运营成本。后续将进一步引入储能系统，抑制光伏发电的波动性，并利用储能的削峰填谷特征提高系统的经济性和促进光伏消纳。