基于EEMD的曲轴随动磨削轮廓误差分析*

房小艳

（上海机床厂有限公司 上海 200093）

曲轴作为发动机的关键零件，其磨削质量直接影响发动机的性能。曲轴随动磨削又称曲轴切点跟踪磨削，通过控制工件的旋转运动（C轴）和砂轮的横向进给运动（X轴），使砂轮外圆和工件被加工表面轮廓始终相切，从而实现偏心圆的加工，该方法具有高效率、高柔性、高精度等特点[1-2]。近年来，汽车和船舶等行业的发展，推动了随动曲轴磨床的应用，同时也对随动曲轴磨床的可靠性和精度稳定性提出了越来越高的要求。

工件表面纹理被称为制造工艺的“指纹”，工程表面特征包括机床性能信息、刀具状态信息以及材料特征信息等[3-4]。曲轴连杆颈随动磨削轮廓误差是随动磨削过程留下的指纹，其中包含了磨床的性能信息、砂轮状态信息以及曲轴材料性能信息。基于曲轴随动磨削工艺的特殊性，磨床C轴、X轴的性能对连杆颈的轮廓误差影响明显；反之，这种磨削工艺产生的轮廓误差包含了明显的随动曲轴磨床的性能信息，特别是C轴、X轴的性能信息。

对机床性能进行分析或预测是工件轮廓误差分析的主要应用之一。针对该种应用，目前已有的轮廓误差分析方法如“傅里叶”变换、“小波”变换都是线性变换，对于轮廓误差非线性非平稳的信号特征，分析结果无法与产生轮廓误差的物理因素直接对应。HUANG验证了即使在最坏的情况下，对经验模态分解（Empirical Mode Decomposition, EMD）得到的特征模态函数（Intrinsic Mode Function, IMF）进行希尔伯特变换所定义的瞬时频率也能与所研究的物理机制相一致[5-6]。

这里首先给出应用聚合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）方法将曲轴轮廓误差进行有效分解，曲轴轮廓误差为闭合数据，为避免边界效应在数据两端进行周期拓展；然后分析了曲轴连杆颈随动磨削轮廓生成原理，给出随动磨床轴运动误差对曲轴轮廓误差影响的计算方法；最后，通过磨削实验进行误差数据采集，对曲轴轮廓误差进行分析，并有效准确地分离出与机床C轴、X轴性能对应的分量。

1 基于EEMD的轮廓误差分解

EMD属于一种基于经验的分解方法[7]，通过筛分的处理过程实现对信号的分解。设任意第i 阶IMF分量为Ci，从X(t)中依次提取出各阶 IMF分量，并从原始信号中去除，直到第n 阶的残余信号r 成为单调函数，不能再筛分出IMF分量，即

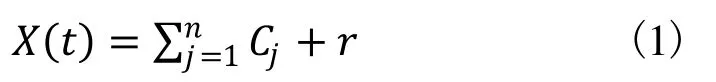
EMD本质上是一个自适应二进制滤波器组的滤波，它能够将白噪声分解为具有不同中心频率的一系列IMF分量。实际应用中，当数据不是纯的白噪声时，分解的一些时间尺度会丢失，造成分解混乱，即模态混叠。由于模态混叠现象的出现，使得各阶IMF分量失去了分解的物理意义。

EEMD可有效弥补 EMD的不足，是对 EMD方法的较大改进[8]。EEMD过程是在原始信号中加入白噪声序列；将加入了白噪声序列分解为IMF分量；每次加入不同的白噪声序列，反复重复前两步；把分解得到各阶IMF的均值作为最终的结果[9]。

基于EEMD的曲轴轮廓误差分解，如图1所示。曲轴轮廓误差为首尾闭合数据，为避免边界效应的影响，在轮廓误差数据两端各扩展一组与原始轮廓误差相同的数据，EEMD分解后取每一阶分量中间的1/3数据作为有效分解结果。EEMD分解得到的分量由高频到低频排布，理论上曲轴轮廓误差数据中不包含由0 UPR （Undulation Per Revolution波数每转）表征的尺寸误差信息以及由1 UPR表征的曲轴轮廓中心偏差信息，将频率小于2 UPR的分量及残余分量与上一阶分量合并作为曲轴轮廓误差分解的最低阶分量，记为C1，设曲轴轮廓误差共分解M阶分量，则Cj（2≤j≤M-1）与EEMD分解的结果依次倒序对应，EEMD分解剩余的高频分量合并作为曲轴轮廓误差分解的最高频成分，记为CM。

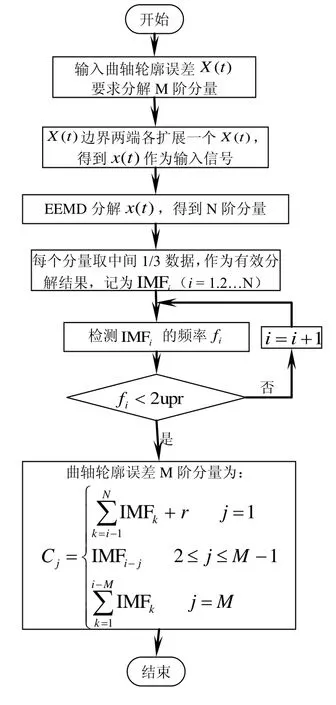
图1 基于EEMD曲轴轮廓误差分解过程

2 轴控制误差对曲轴轮廓误差的影响

曲轴连杆颈的随动磨削轮廓是由砂轮往复运动跟随曲轴的回转运动，在磨削过程中砂轮始终与连杆颈保持相切而形成的。理想状态下，假设曲轴连杆颈为标准圆轮廓，切点即磨削点G在连杆颈中心 Op与砂轮中心 Ogw的连线上，其磨削运动原理如图2所示，曲轴在机床工件驱动轴C轴带动下，连杆颈绕主轴颈中心O旋转，砂轮沿X轴作往复跟踪运动，实现曲轴连杆颈的磨削。

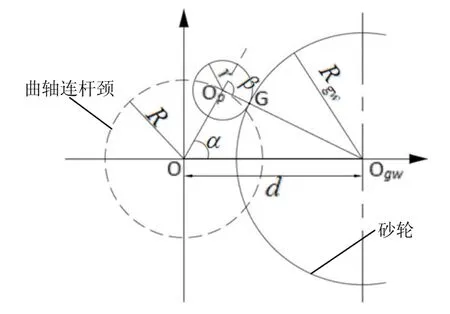
图2 理想状态下曲轴随动磨削运动原理图

(d ,α)表征机床X轴、C轴的运动控制位置信息，决定连杆颈的轮廓，简称轮廓控制点，对应连杆颈的轮廓点(r ,β)，即(r ,β)表征连杆颈的轮廓信息。

轮廓控制方程为：

由式(2)变换得：

根据几何关系有：

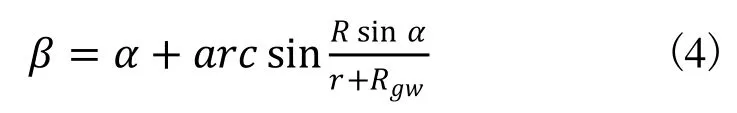
式(3)代入式(4)得：

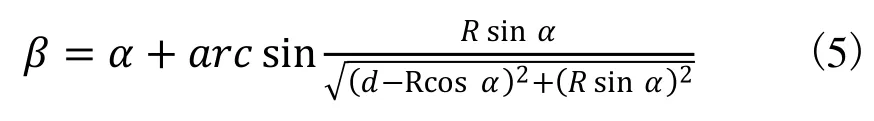
式中，d是砂轮沿X轴往复运动，砂轮中心Ogw到曲轴回转中心O的距离；R 是连杆颈偏心距，即连杆颈中心 Op到曲轴回转中心O的距离；r 是连杆颈半径，即磨削点G到连杆颈中心 Op的距离；Rgw是砂轮半径； 是 OOp与 OOgw的夹角，即C轴控制曲轴回转的角度； 是 OOp的延长线与 OpOgw的夹角，即磨削点经过的圆弧所对应的角度。

磨削工件时，根据轮廓控制方程得到理论的磨削运动控制方程：

式(2)～式(7)中，R、r 为运动控制参数，是常数；当选择超硬砂轮，如 CBN砂轮，其磨损量非常小可以忽略不计，此处 Rgw可以视为常数。

机床数控系统根据式(6)～式(7)控制C轴、X轴运动，磨削曲轴连杆颈，只有机床C轴、X轴的实际运动位置准确无误地满足等式要求，才能磨削得到理论的标准圆形，但实际加工中C轴、X轴的运动控制必然存在误差，这样使得磨削得到的连杆颈并不是一个理论的圆形。

为了更准确地得到曲轴连杆颈的磨削轮廓生成原理，即机床位置控制信息与曲轴连杆颈的轮廓信息之间的关系，将坐标系建立在连杆颈上；若不考虑曲轴的弹性变形恢复，可以将磨削过程视为砂轮绕连杆颈回转，则砂轮轨迹的内包络线则为磨削形成的连杆颈的轮廓，如图3所示。

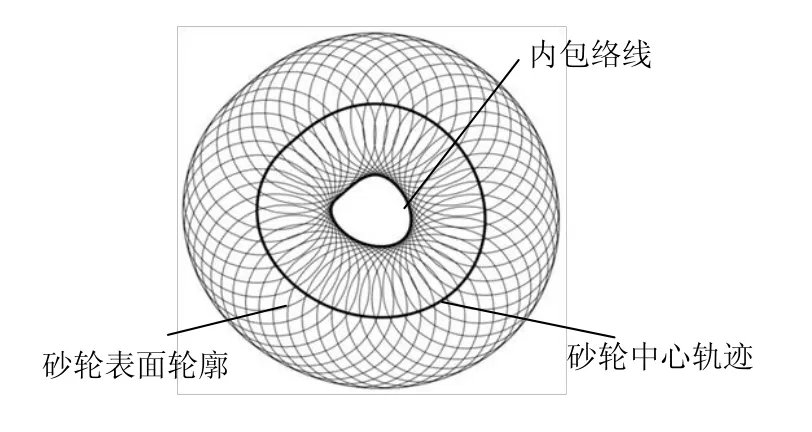
图3 磨削轮廓生成原理示意图

根据上述原理，由机床实际轮廓控制点即机床C轴、X轴的实际坐标位置磨削形成得到的曲轴连杆颈轮廓如图4所示。

图4 连杆颈非圆时其切点跟踪磨削运动关系原理图

在x1Oy1坐标系下，砂轮中心轨迹点对应的极坐标为 (d ,α)，直角坐标为 (dcosα ,dsinα)；在xOpy坐标系下，砂轮中心对应的极坐标点为 (ρ ,θ)，直角坐标为 (dcosα-R ,dsinα)，则：

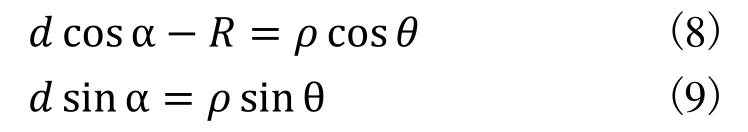
根据式(8) 、式(9)有：

设 ρ(θ)为砂轮中心轨迹上已采集的离散点(ρ ,θ)通过样条曲线拟合得到的轨迹函数，根据几何关系有：

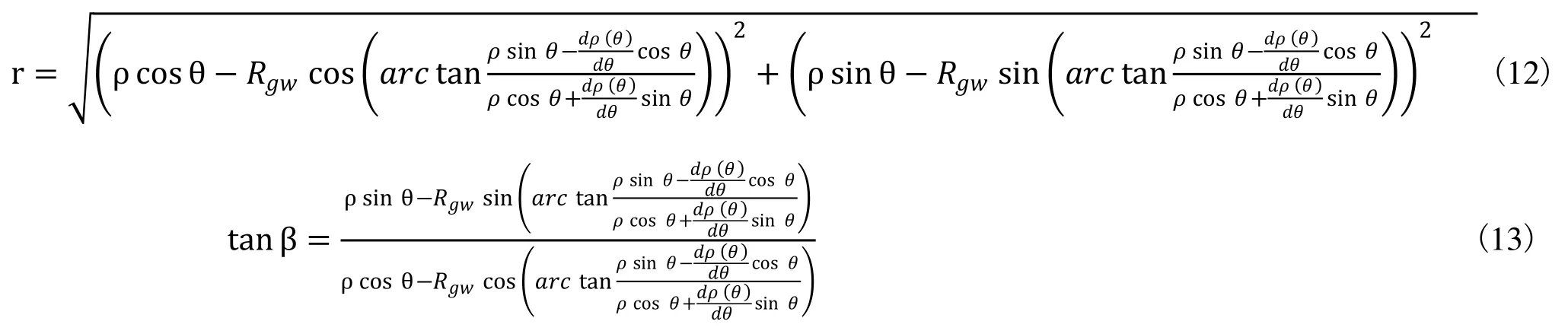
( r,β）是曲轴连杆颈在曲轴回转中心为O、连杆颈名义中心为Op、相位基准为X轴正方向时的轮廓信息，由曲轴连杆颈轮廓以最小二乘法拟合得到基圆，实际轮廓与基圆轮廓的误差记为轮廓误差[10]。可见，影响曲轴连杆颈轮廓误差的主要因素直观地体现在机床X轴、C轴的控制误差上，即实际位置控制值与理论值不可避免的存在偏差，而其基本几何关系建立在图 7及式(10)～式(13)所表达的连杆颈为非圆时其切点跟踪磨削运动关系原理基础上。轴控制误差引起曲轴轮廓误差的计算流程如图5所示。

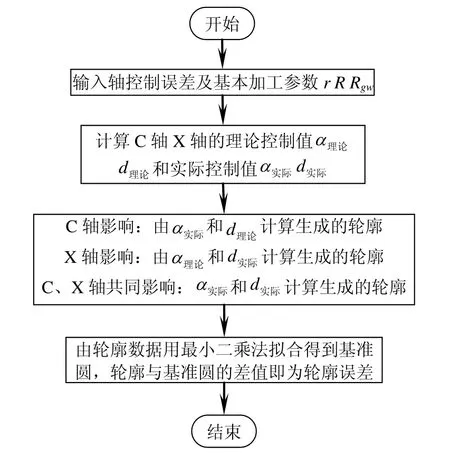
图5 轴控制误差引起的曲轴轮廓误差计算流程

3 误差数据采集及分析

应用数控随动曲轴磨床磨削加工曲轴连杆颈，磨削过程中利用数控系统跟踪功能同步采集机床C、X轴运动控制误差，并测量磨削后的曲轴连杆颈轮廓误差。

磨削用机床为H405-BF数控随动曲轴磨床，机床数控系统为西门子840D，采用CBN砂轮，其半径299.970 mm；工件为LTG生产线的曲轴，连杆颈直径：Φ48.040 mm，偏心距：49.000 mm；磨削采用恒转速磨削，工件转速50r/min。

机床C、X轴运动控制误差采样周期4 ms，结果如图6、图7所示；磨削后在ADCOLE 1200SH曲轴综合测量仪上测量曲轴连杆颈轮廓误差，带高斯滤波器，截止频率50 UPR，一周360°测量1440点，测量数据如图8所示。

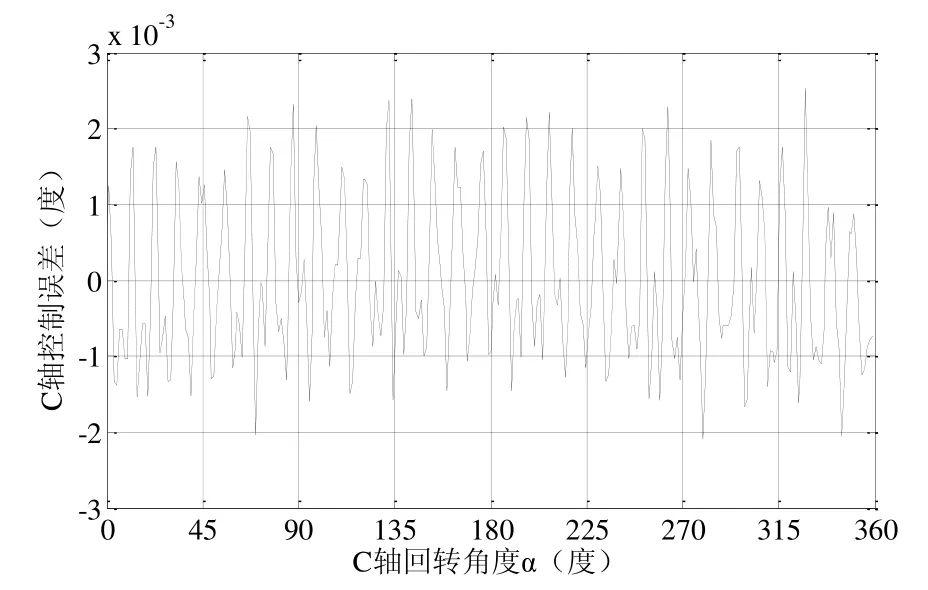
图6 C轴运动控制误差采集值

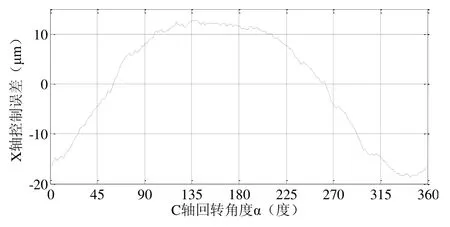
图7 X轴运动误差采集值

图8 曲轴连杆颈轮廓误差测量值

忽略砂轮架、砂轮及砂轮主轴的变形，C、X轴的运动控制信息可以等效为砂轮中心轨迹信息。根据曲轴连杆颈随动磨削轮廓生成原理，由砂轮中心轨迹可以得到磨削工件轮廓。数据采集过程中，测量曲轴连杆颈随动磨削轮廓误差采用50 UPR高斯滤波，为增加数据可比性，将曲轴控制误差计算得到的轮廓误差做相同的滤波处理。由C轴运动控制误差引起的曲轴连杆颈轮廓误差如图9所示，由X轴运动控制误差引起的曲轴连杆颈轮廓误差如图10所示。

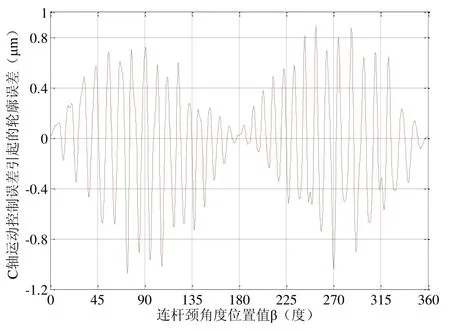
图9 C轴运动控制误差引起的轮廓误差计算结果

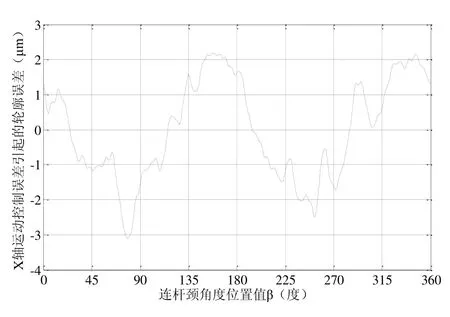
图10 X轴运动控制误差引起的轮廓误差计算结果

将测量得到的曲轴连杆颈轮廓误差数据应用EEMD方法根据图1所示的过程进行分解，要求分解6阶分量，结果如图11所示，EEMD分解结果中有效成分 IMF2-IMF8，IMF1为添加白噪声引入的高频干扰。根据低频成分判断标准 IMF6-IMF8及残余分量求和作为曲轴轮廓误差分解的低频成分。

经对比可以得到C4与C5分量和与由C轴运动控制误差引起的轮廓误差相匹配，如图12所示；C1、C2和C3三者之和与由X轴运动控制误差引起的轮廓误差相匹配，如图13所示，即通过EEMD分解的方法有效地从曲轴连杆颈轮廓误差中分离出与机床C、X轴相对应的误差分量。

图12 曲轴轮廓误差中受C轴运动控制误差影响的分量

图13 曲轴轮廓误差中受X轴运动控制误差影响的分量

4 结语

(1)选用EEMD方法，避免了曲轴轮廓误差分解模态混叠的问题；通过边界周期扩展，避免了闭合轮廓边界失真的问题；合理地设置了低频成分判别方法，提取了有效低频成分，实现曲轴轮廓误差从低频到高频的有效分解。

(2)通过坐标变换，给出了随动磨削轮廓为非圆时精确的工件轮廓生成原理，为轴运动控制误差对曲轴轮廓误差的影响提供了计算依据。

(3)通过磨削实验验证，将测得的随动磨削曲轴轮廓误差数据进行分解，根据轴运动控制误差结合加工信息计算得到其引起的曲轴轮廓误差信息，经对比，从随动磨削的轮廓误差数据中有效地分离出与C轴、X轴性能对应的分量。探索出一种通过工件随动磨削轮廓误差预测机床关键功能部件性能的方法。

(4)在曲轴自动生产线上，各工位加工结果一直处于抽检监控状态，利用其中的曲轴随动磨削轮廓误差数据分析判断出随动曲轴磨床C轴、X轴的性能或者性能变化趋势，可以作为关键功能部件预防性维修的依据，对生产线稳定可靠运转有较大指导意义。