多种服役环境下航空铝合金疲劳裂纹扩展行为

颜光耀，刘治国，穆志韬，李旭东

(海军航空大学青岛校区 航空机械系， 山东 青岛 266041)

铝合金由于其比强度高、加工性能好等优点，广泛应用于航空工业领域。某些飞行器机身使用LD2CS铝合金，且要常年转场于环境差异较大的多个机场，易受到不同环境的腐蚀。腐蚀损伤的存在会使铝合金结构件更易断裂失效，开展腐蚀损伤对铝合金结构件剩余强度和疲劳断裂性能的评估工作至关重要。LD2CS铝合金在转场环境初期的主要腐蚀损伤形式是点蚀，很多学者量化研究了铝合金点蚀形貌对材料疲劳性能的影响。文献[1-4]提出用蚀坑深度值作为铝合金在腐蚀溶液中的疲劳性能，从而得到了不同腐蚀时期蚀坑深度与疲劳寿命的对应关系，依此进行腐蚀疲劳寿命的预测。张有宏等[5]定义了腐蚀损伤度，用来表征点蚀的表面积所占考核区域的比重，并得到了腐蚀损伤度与疲劳寿命的表达式。文献[6-9]将腐蚀坑等效成半圆形或半椭圆形表面裂纹，将腐蚀疲劳问题转化为有预制表面裂纹的疲劳裂纹扩展问题进行研究。文献[10-12]从工程应用角度，建立了预腐蚀影响系数曲线的统计分析方法，并对其通用性进行了分析。蔡剑等[13]、马少华等[14]和王池权等[15]学者研究了不同腐蚀环境下铝合金材料的腐蚀疲劳性能，从环境类型的角度得到不同环境对试件疲劳性能的影响。

由以往研究可知，关于铝合金腐蚀损伤对其疲劳性能的影响往往从单一点蚀形貌表征量入手，得到的经验公式存在片面性，关于腐蚀损伤表征量对裂纹扩展行为的贡献度也没有过多论述。本文利用平均影响值(Mean Impact Value,MIV)方法[16]对9个腐蚀损伤表征量进行筛选，得到三个最重要的腐蚀损伤表征量，通过加权平均的方法得到腐蚀损伤综合指标α，并依此开展腐蚀损伤对裂纹扩展行为的影响。

文献[17-22]利用扫描电子显微镜原位观测技术，研究了预腐蚀疲劳情况下的物理短裂纹扩展行为，发现短裂纹的扩展路线受到临近腐蚀坑尺寸和晶粒内部作用力的影响，并得到裂纹扩展速率与局部应力应变场的参数相关的经验表达式。由于对铝合金结构件的损伤程度不同，转场环境下的贯穿型裂纹并不适合从局部腐蚀损伤对裂纹尖端的影响这一角度进行研究。本文在计算出腐蚀损伤综合指标α后，对比分析了不同加速腐蚀年限下的裂纹扩展速率，根据相应腐蚀年限的裂纹扩展特点，定义了腐蚀加速系数Ω(α)，并通过工程拟合得到经过腐蚀加速系数Ω(α)修正的Paris公式，最后利用试验数据验证了依据腐蚀损伤综合指标建立的腐蚀加速系数的有效性。

1 腐蚀与疲劳试验

试验件为狗骨状的LD2CS铝合金，尺寸图与实物图如图1所示。飞行器所在机场停放的时间取平均得到加速腐蚀试验总谱[23-27]，如图2所示。

(a) 试验件尺寸图(厚度：t=3 mm)(a) Test piece dimension (thickness: t=3 mm)

(b) 试验件实物图(b) Test piece object图1 LD2CS铝合金试验件Fig.1 Aluminum alloy LD2CS test piece

图2 LD2CS铝合金加速腐蚀试验环境谱Fig.2 Accelerate corrosion spectrum of engine aluminum alloy LD2CS

由图2可知，LD2CS铝合金加速腐蚀68.55 h相当于在机场转场环境中使用一年的腐蚀损伤量。根据谱中参数要求，配制浸泡试件用的酸性溶液：在质量浓度为5%的NaCl溶液中滴入浓H2SO4，使溶液的pH=4±0.2。设定红外烤灯烘烤条件：相对湿度RH=90%～95%，温度T=(40±2)℃。将试验件编号后依序置于ZJF-45G周浸试验箱，依据加速腐蚀试验要求，对试件分批次进行一次循环为浸泡3.6 min烘烤9.1 min，324次循环为一个当量加速腐蚀日历年限，最长20个相应当量年限的加速腐蚀试验。每隔2个当量加速腐蚀年限，将相应组别的试验件取出，利用KH-7700形貌检测显微镜对有效受力区域的蚀坑形貌进行观测和统计分析，图3所示为4个不同加速腐蚀年限下典型腐蚀区域的形貌图。

利用电火花线切割技术预制中心贯穿裂纹，长度为1 mm，如图1(a)所示。在MTS-810电液伺服疲劳试验平台上进行疲劳拉伸试验，每隔2000次循环，用KH-7700形貌检测显微镜测量相应裂纹长度c，c为预制裂纹长度的一半加上裂纹扩展路径垂直于加载方向上的投影长度。疲劳试验在MTS-810疲劳试验机上进行，环境温度为室温，加载波形为正弦波，采取轴向等幅加载方式，应力比R=0.06，加载频率f=10 Hz，最大应力σmax=267 MPa。

(a) 典型蚀坑三维形貌(a) Three-dimensional morphology of typical pit

(b) 典型蚀坑面积测量图(b) Measurement chart of typical pit surface area

(c) 蚀坑宽度与深度测量图(c) Measurement chart of typical pit width and depth图3 典型蚀坑腐蚀形貌及测量图Fig.3 Morphologies and measurement charts of typical pit corrosion

2 试验结果及讨论

2.1 腐蚀损伤综合指标

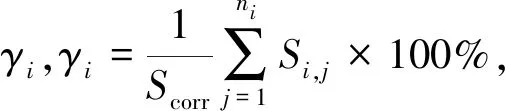
上述各腐蚀损伤表征量对疲劳裂纹扩展行为的影响程度不同，如果将不重要的量引入裂纹扩展模型，会增加模型的复杂性和计算误差，因此需要对腐蚀损伤表征量进行筛选。

MIV方法可以表示神经网络中权重矩阵的变化情况并能准确评价输入变量对输出变量的相关性大小。具体计算过程为：网络学习结束时，将学习样本中的自变量特征在原值基础上增减10%，重新组成学习样本，用已建成的网络进行训练，将得到的新的两个仿真结果与真实结果相减，得到自变量变动后对输出产生的影响变化值(Impact Value，IV)，最后将IV按照观测数取平均得到该自变量对网络输出的MIV值，符号代表相关的方向，绝对值代表所占比重的大小。根据MIV的绝对值大小，对自变量的影响程度进行排序，从而实现变量的筛选。

将9个不同加速腐蚀年限下的腐蚀损伤表征量作为神经网络的输入变量，输出为相应腐蚀年限下的疲劳裂纹扩展寿命，按照MIV的训练过程，得到不同加速腐蚀年限下的腐蚀损伤表征量MIV的绝对值，取平均值得到如表1所示的上述9个腐蚀损伤表征量MIV的绝对值。

由表1可知，对裂纹扩展寿命的影响程度由大到小排序为：dmax,i，dave,i，γi，amax,i，aave,i，Smax,i，Vave,i，Save,i，Vmax,i。可以看出，dmax,i，dave,i，γi，amax,i，aave,i的MIV值相对较大。又因为同一腐蚀条件下的蚀坑深度服从正态分布N～(μ,σ2)，且有[28]：

表1 腐蚀损伤表征量对应的MIV绝对值

dmax,i=nσ+dave,i

(1)

amax,i=nσ+aave,i

(2)

式中，n为常数，所以选择最大蚀坑深度dmax,i，最大蚀坑宽度amax,i和点蚀率γi作为衡量腐蚀损伤对裂纹扩展寿命影响程度的三大指标。

上述三种腐蚀表征量随加速腐蚀年限的变化均很好地符合幂函数规律，如图4(a)～(c)所示，分别为dmax,i，amax,i和γi随加速腐蚀年限变化的散点图和拟合曲线。

因各腐蚀损伤指标的时间变化规律相似，但量纲不同，需要对其分别进行归一化处理，公式定义如下：

yi=xi/xmax

(3)

式中，yi为归一化后第i个加速腐蚀日历年限下的腐蚀损伤量，xi为第i个加速腐蚀日历年限下的腐蚀损伤测量值，xmax为相应腐蚀损伤指标的最大测量值。

三大腐蚀损伤表征量的归一化量随时间变化的幂函数与实际测量值的幂函数对比发现，拟合函数的相关性与参数b不变，只有参数a改变，各表征量拟合曲线的参数如表2所示。

(a) 最大蚀坑深度和加速腐蚀年限的关系(a) Maximum pit depth versus accelerated corrosion year

(b) 最大蚀坑宽度和加速腐蚀年限的关系(b) Maximum pit width versus accelerated corrosion year

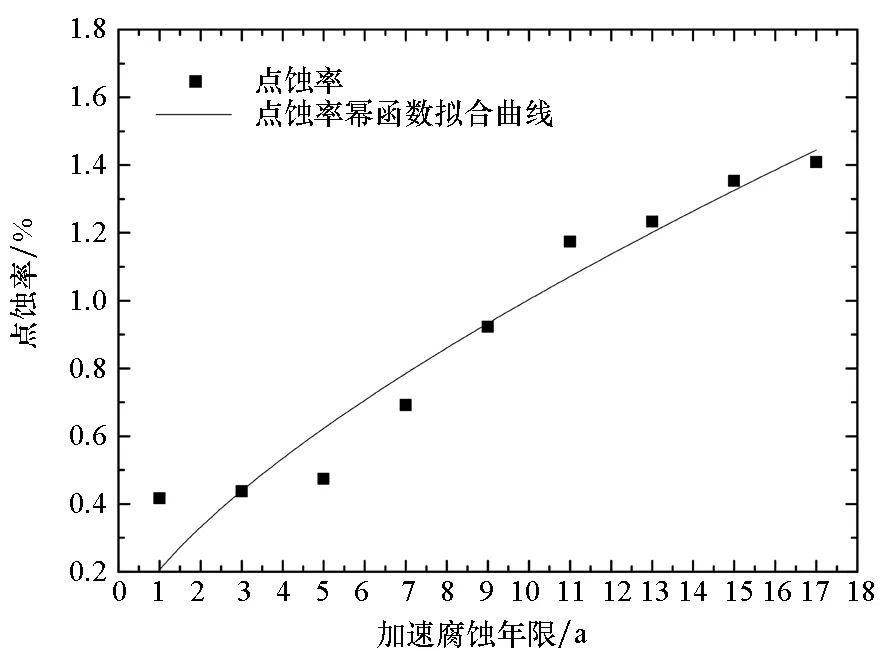
(c) 点蚀率和加速腐蚀年限的关系(c) Pit surface rate versus accelerated corrosion year图4 三大腐蚀损伤指标随加速腐蚀年限变化的拟合曲线Fig.4 Fitting curves of three important corrosion characterization factors versus accelerated corrosion year

表2 三大腐蚀损伤表征量随腐蚀年限变化的参数拟合结果Tab.2 Parameter fitting results of three corrosion damage characterization quantities varying with corrosion years

利用加权平均法得到基于筛选出的三大腐蚀损伤表征量的腐蚀损伤综合表征指标α(t)，其公式如下：

(4)

其中：MIVdmax为腐蚀坑最大宽度对应的MIV绝对值；MIVamax为腐蚀坑最大宽度对应的MIV绝对值；MIVγ为点蚀率对应的MIV绝对值。将其代入表1中相应MIV值得到腐蚀损伤综合指标(无量纲)随加速腐蚀年限变化的动力学方程为：

α(t)=0.421ydmax+0.237yamax+0.342yγ

=0.123t0.436+0.017t0.945+0.050t0.687，1a≤t≤17a

(5)

2.2 腐蚀损伤对疲劳裂纹扩展行为的影响

通过试验观测得到c-N曲线，对其进行差分计算可以得到dc/dN-N曲线，即裂纹扩展速率变化曲线。由观测可知，裂纹扩展距离低于100 μm时，扩展速率波动性较强，属于短裂纹扩展时期，本文不予考虑。根据Paris公式，(dc/dN)i=Ci(ΔK)mi，其中Ci和mi分别为第i个加速腐蚀年限下的拟合参数，得出不同加速腐蚀年限下的长裂纹扩展速率随应力强度因子变程ΔK的变化曲线，其中ΔK可通过查阅《应力强度因子手册》获得。将dc/dN-ΔK曲线的自变量和因变量进行双对数处理并对不同加速腐蚀年限下的裂纹扩展速度进行直线拟合，图5所示为加速腐蚀0 a，5 a，11 a和17 a后的双对数坐标图。

图5 疲劳裂纹扩展ln(dc/dN)-lnΔK关系图Fig.5 Relationship between ln(dc/dN) and lnΔK

从图5可知，用斜率均为4的直线拟合不同加速腐蚀年限的裂纹扩展速率双对数散点图，有很强的相关性。随着腐蚀损伤的逐年加重，裂纹扩展速率明显提高。表3给出了上述4个不同腐蚀时间下的Paris公式拟合参数。

表3 不同加速腐蚀年限裂纹扩展速率Paris公式拟合Tab.3 Parameters value of Paris model for different accelerated corrosion years

从表3可知，加速腐蚀17 a后，裂纹扩展速率增加了约10倍。定义腐蚀加速系数Ω(α)对Paris公式进行修正，其中α为腐蚀损伤综合指标，令Ci=Ω(α)·C0，图6给出了腐蚀加速系数Ω(α)与腐蚀损伤综合指标α的拟合关系，由图可知当α≥0时，腐蚀加速系数的拟合函数为：

Ω(α)=-14.459α3+24.075α2-0.44α+1.035

(6)

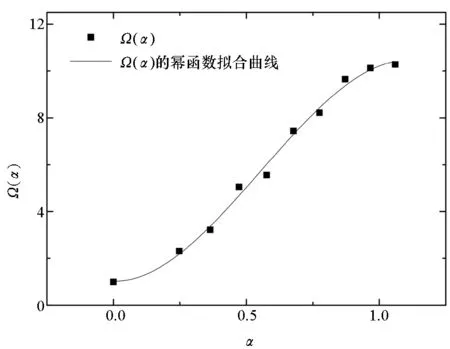
图6 腐蚀加速系数Ω(α)与腐蚀损伤综合指标α的对应关系Fig.6 Corresponding relationship between corrosion acceleration coefficient Ω(α) and comprehensive index of corrosion damage α

由图6可知，在加速腐蚀0～17 a间，腐蚀加速系数Ω(α)随腐蚀损伤综合指标α单调递增，即裂纹扩展速率随着腐蚀损伤程度的增加而增大。三次拟合曲线的切率先增大后减小，说明扩展速率随着腐蚀损伤程度的增加而增长缓慢，在产生剥蚀之前，裂纹扩展速率最大值很可能维持在约10倍的未腐蚀试件的裂纹扩展速率。

2.3 腐蚀加速系数的有效性验证

分别统计观测加速腐蚀第18 a、19 a、20 a的蚀坑最大深度值，蚀坑最大宽度值和点蚀率，将其代入式(4)，求得相应腐蚀损伤综合指标α18、α19、α20，并将其代入式(6)计算得到相应的腐蚀加速系数预测值，与试验获得的加速腐蚀第18 a、19 a、20 a时的腐蚀加速系数进行对比，对比结果如表4所示。

由表4可知，预测相对误差均小于10%，预测结果较好且偏保守。因此，式(6)适用于计算影响裂纹扩展速率的腐蚀加速系数。将Ω(α)代入未腐蚀的LD2CS铝合金中心贯穿裂纹板的Paris公式，可求出飞行器转场环境下不同裂纹长度时0～20 a的裂纹扩展速率，获得的腐蚀损伤综合指标α也可用于其他机场环境的裂纹扩展行为研究。

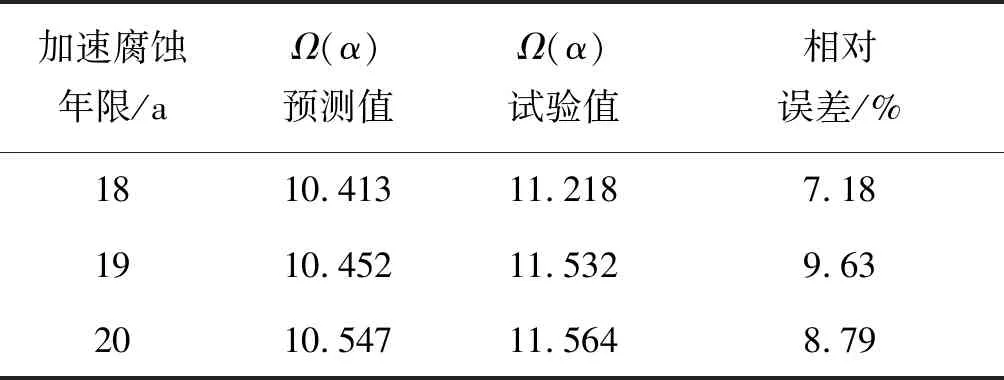
表4 腐蚀加速系数Ω(α)预测结果

3 结论

对预腐蚀的LD2CS铝合金试件预制中心裂纹并进行疲劳裂纹扩展试验，得到主要结论如下：

1)由MIV方法得到对裂纹扩展寿命影响最大的三个腐蚀损伤表征量：蚀坑最大深度、蚀坑最大宽度和点蚀率。

2)对上述三种腐蚀损伤表征量进行归一化和加权平均方法的处理，得到腐蚀损伤综合指标α的动力学方程。

3)随着腐蚀损伤程度的增加，腐蚀损伤对疲劳裂纹扩展的加速作用也越来越明显。定义腐蚀加速系数Ω(α)，将转场环境下Paris公式修正为(dc/dN)i=Ω(αi)C0(ΔK)m0，得到Ω(α)的多项式表达式。

4)利用加速腐蚀18 a、19 a、20 a时统计观测三个重要的腐蚀损伤表征量和相应年限的裂纹扩展速率对式(4)进行有效性验证，得到腐蚀加速系数预测值的相对误差均小于10%，从工程实用角度表明，式(4)适于定量表现LD2CS铝合金有限薄板的中央贯穿裂纹随腐蚀损伤程度增加裂纹扩展速率增大的现象。

本文只研究了铝合金点蚀损伤对长裂纹扩展速率的影响，裂纹萌生及短裂纹扩展期和其他腐蚀形式对航空铝合金结构件的腐蚀疲劳寿命的影响同样严重，后续会继续开展多种腐蚀形式对疲劳裂纹不同扩展时期影响的研究。