5层空气孔单实芯纯石英光子晶体光纤仿真
高 朋, 韩 博, 刘松伟
(沈阳师范大学 物理科学与技术学院, 沈阳 110034)
迄今为止,人们已经设计出了许多结构新颖的光子晶体光纤(photonic crystal fiber,PCF),但由于制备工艺不能真正运用到传感器的实验应用当中,无法适应光纤传感技术的快速发展需求,所以对PCF结构的仿真分析极其重要。目前,人们已做了大量的理论性分析工作,为后续的众多实验研究进行理论的铺垫。2014年,李彦等[1]为研究空芯PCF磁敏感性,利用Comsol软件对HC-1550-2 空芯PCF的Verdet常数进行仿真计算,验证了PCF在降低磁敏感性方面的优势;2015年李建华等[2]通过建立谐振式PCF陀螺环路模型来减小系统中相对频率噪声对随机游走系数的影响;顾达等[3]运用全矢量有限元法,利用COMSOL软件设计了一种新型THz波PCF,并对该光纤的损耗、色散特性进行数值计算与优化;2016年,王旭等[4]建立了空芯带隙型PCF残余双折射理论分析模型,采用全矢量有限元法,通过搭建实验平台对光纤双折射的波长依赖性和温度稳定性进行探究;杨汉瑞等[5]提出一种风扇型包层结构的大模场PCF,仿真分析其空气孔间距和空气孔直径对光纤性能参数的影响,光纤能够在1.3~2.0 μm工作波长下进行单模传输,并可获得104μm2量级的大模场面积;2017年,雷刚[6]通过改变光纤的结构参数,设计的光纤模式双折射度达到10-2量级,限制损耗可控制在10-7量级,为高速长距离光纤通信的实际应用奠定了基础;冯迪等[7]将PCF端面研磨过程简化为单颗磨粒切削单孔壁,应用有限元法建立了数值仿真模型,分析了裂纹损伤产生的机理;张学典等[8]设计了正四边形晶格空气孔排列的PCF,在纤芯附近引入不同的微结构空气孔,运用全矢量有限元差分法,对不同微结构的PCF的模式有效折射率、限制损耗等特性参数进行仿真与分析;杨勋恩等[9]采用全矢量有限元法,研究了空气孔为正九边形周期性排列的全内反射型PCF的温度传感特性,得到有效折射率和限制损耗的大小与温度成反比关系的结论;2018年,宋凝芳等[10]针对实芯保偏PCF散射损耗,建立光纤散射模型,仿真计算出散射损耗为0.179 dB/km,曾春香等[11]设计了一种椭圆空气孔缺陷PCF,采用全矢量有限元法结合完美匹配层吸收边界条件对该结构的模场分布、双折射、模有效面积等特性进行数值计算分析,在波长为1 550 nm,孔间距为1.3 μm时,可获得10-2数量级的双折射;荣耕辉等[12]设计了一种高双折射结构的PCF,建立了对应的数学模型并采用全矢量有限元法对该结构的模场强度、有效折射率、双折射等特性进行分析,在1 550 nm处可以获得7.66×10-3的双折射和低至12 ps/(nm·km)的色散值;李天琦等[13]利用单透镜耦合方式对棒状PCF进行了耦合实验,分别模拟计算了当耦合透镜F=103.26 mm时耦合效率与透镜位置的关系,以及当透镜与光纤端面的距离为120 mm时耦合效率与透镜焦距的关系; Yang等[14]提出一种PCF设计,用ENZ材料填充包层中的选定气孔,显着增强了双折射,宽频带上具有高于0.1的双折射和低于0.01 cm-1的损耗; Hu等[15]制造了异质结构包层实心光子带隙光纤(HCSC-PBGF),支持宽带隙下的强芯模和包层模传输,对异质结构包层设计进行了理论分析; Liu等[16]报道了一种中心凹陷和包层沟槽掺有Yb的光纤,通过改进化学气相沉积工艺和溶液掺杂技术制造的,模拟结果表明,纤芯直径为40 μm,数值孔径为0.043的光纤在1 080 nm处的有效模面积为1 217 μm2。
本文选用了当前制备工艺较为成熟的单芯全内反射PCF,此类光纤制备技术趋于成熟,成本有所下降,国内已有少数几家机构具备制备能力。单实芯纯石英PCF属于全内反射型PCF,其纤芯区域为纯石英材料,且只有一个纤芯,包层区域是周期性分布的空气孔,是最早出现也是目前制备工艺最成熟的PCF之一,将其运用与传感器的制作,具有成本低廉、性能稳定等优势,可以推动PCF传感器的商用化进程。在众多传感技术方案中,运用此类光纤搭建的传感系统,实验效果明显。因此,有必要先对其的基本理论特性进行分析,本节主要针对5层空气孔的单实芯全内反射PCF,顶角空气孔缺失的结构进行模场和特性的分析。
1 结构模型建立与网格划分
目前国内一些机构具备了拉制全内反射PCF的能力,成本日趋降低,本文选用了武汉国家光电实验室拉制的5层空气孔的单实芯纯石英PCF,其电子显微镜下端面结构如图1所示,相关参数如表1所示。

表1 单实芯纯石英PCF参数Table 1 The parameters of single solid core of pure silica PCF

图1 单实芯纯石英PCF端面结构图Fig.1 The cross section scheme of pure silica PCF with single solid core
根据此结构可以看出,此PCF的横截面面空气孔具有5层正六边形结构,由于制备需要,最外层正六边形的顶角缺失一个空气孔。利用COMSOL 3.5对其进行有限元分析,首先要建立光纤的几何结构模型,几何模型中包层直径设定为125.20 μm,空气孔间距设定为7.67 μm,空气孔直径为4.88 μm,空气孔层数为5层,最外侧正六边形顶角无空气孔,利用COMSOL3.5的工具建立了单实芯纯石英PCF横截面的几何模型。并且选择石英作为衬底材料,折射率设定为1.444 3,利用软件工具对几何模型进行网格划分,使其区域离散化。
在设定网格参数时,可以选择软件中默认网格尺寸,也可根据计算内存情况和结构复杂程度,来自定义网格密度。本次网格划分以后,三角形网格单元数为10 424个,边界单元数为2 016个。
2 基模与包层模模场分布
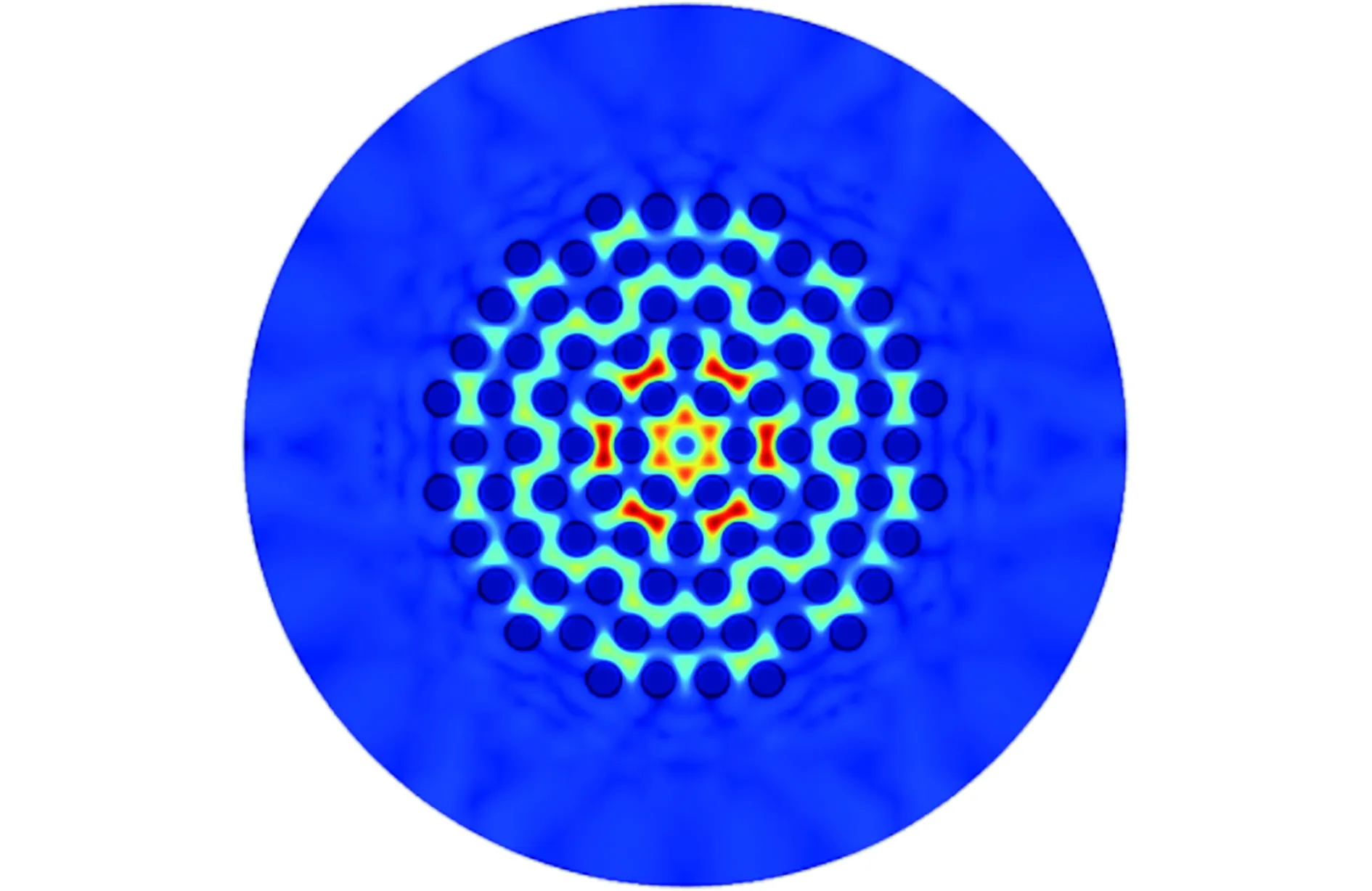
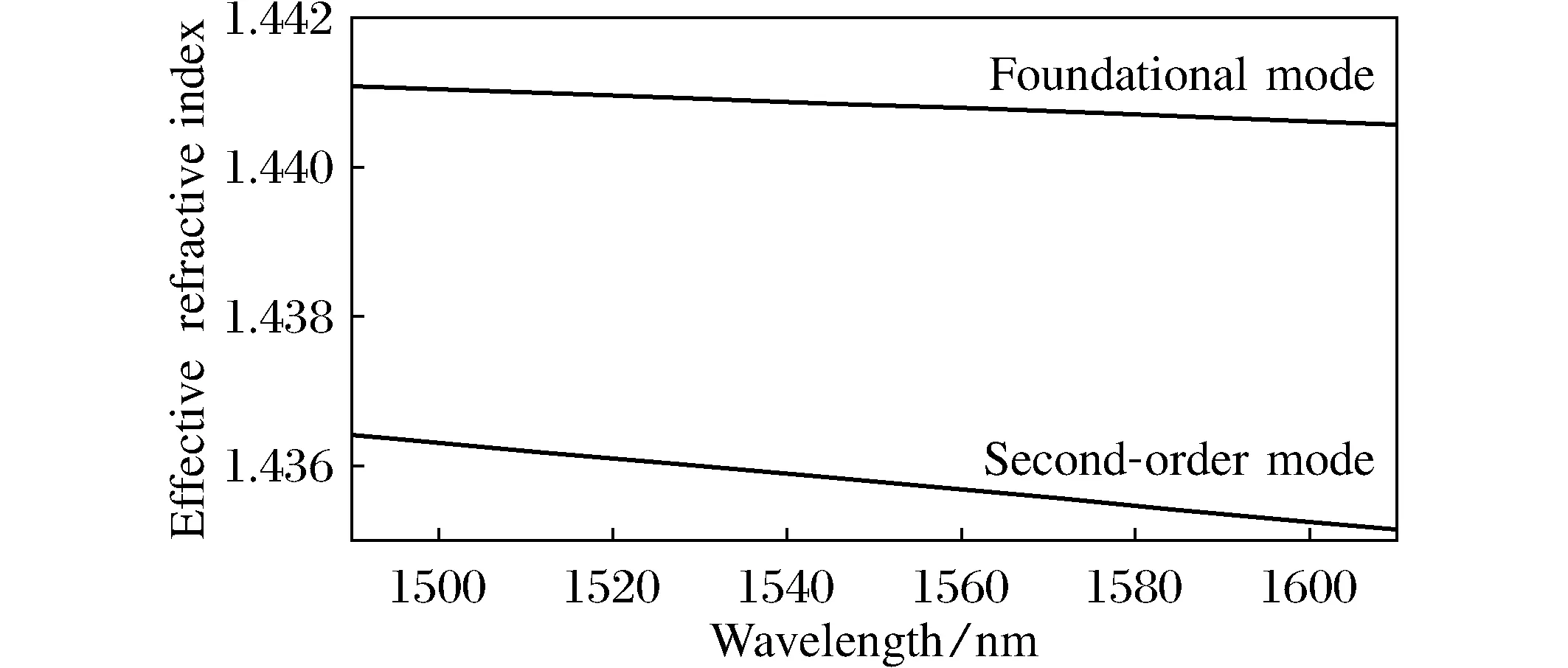
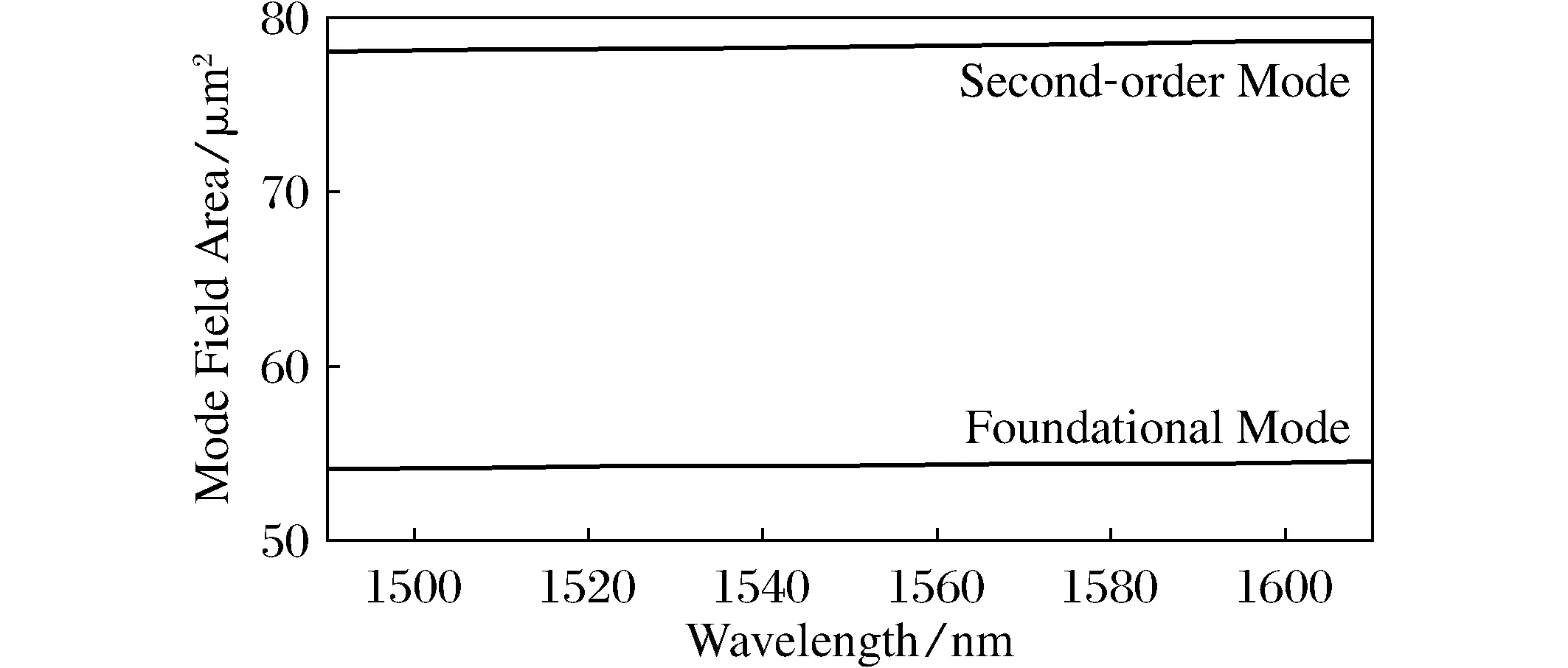
根据光纤的性质可知,当模式折射率nclad 利用完美匹配层作为边界条件,运用COMSOL软件对单实芯纯石英PCF纤芯区域的模场进行仿真,图2是在1 550 nm处基模和二阶模的模场分布情况。从图中可以看出,单实芯纯石英PCF的纤芯模场具有多模的特性。图2(a)和图2(b)分别为基模的归一化电场和磁场分布的二维和三维图,从图中可以看出,基模模场的能量主要集中在纤芯的中心,模场成类圆形,在1 550 nm处的有效折射率为1.440 9;图2(c)和图2(d)分别为二阶模的归一化电场和磁场分布的二维和三维图,从图中看出,二阶模的模场能量沿径向向包层区域外延伸,模场中心能量衰减,并且与基模的模场正交,在1 550 nm处的有效折射率为1.435 7。由此可以看出,基模的有效折射率相对于二阶模具有较大的有效折射率。 (a) 基模电场分布图; (b) 基模磁场分布图; (c) 二阶模电场分布图; (d) 二阶模磁场分布图.图2 1 550 nm下单实芯纯石英PCF纤芯模场分布Fig.2 Mode field distribution of pure silica PCF with a single solid core at 1 550 nm 图3 单实芯纯石英PCF包层模场分布Fig.3 Mode field distribution of the cladding of pure silica PCF with single solid core 图4 单实芯纯石英PCF有效折射率随波长的变化Fig.4 The variation of effective refractive index of a single solid core pure silica PCF with wavelength 此外,对单实芯纯石英PCF的包层的某高阶模式的电场分布进行了模拟,电场能量分布情况如图3所示。从图3中可看出,单实芯纯石英PCF的包层模场呈现多模的特性,模场能量在纤芯的中心区域十分微弱,而在纤芯的外延区域与第1层空气孔交界处,存在着一定的能量分布,较大的能量分布主要存在于第1层空气孔和第2层空气孔之间,第2层空气孔向外延伸的区域则能量很弱。当然,这只是包层模某一高阶模的能量分布情况,而包层模的模场分布还与外场的激发条件有关,高阶模较多,模场分布十分复杂,利用包层模实现传感需要各种外加条件来实现。 3 有效折射率的计算 光纤中某个传输模式的折射率n需要满足nclad 从图4中可看出,在1 500~1 600 nm的波长范围内,在相同波长下基模的有效折射率总是大于二阶模。随着波长的增加,纤芯的基模和二阶模的有效折射率均会随之降低,而基模有效折射率的变化趋势较为平缓,变化率为4×10-6/nm,二阶模的有效折射率的变化趋势较为陡峭,变化率为1×10-5/nm。这是因为随着波长增加,模场变大,有更多的能量泄露到空气孔中,相对于二阶模,基模的有效折射率相对稳定。 有效模场面积Aeff,是PCF的主要特性之一,对PCF传感器性能具有一定的影响,模场大小决定了不同模式之间耦合效率的高低。 有效模场面积的公式为 (1) 其中E(x,y)为光传播时的横向电场分布。 图5 单实芯纯石英PCF模场面积随波长的变化Fig.5 The variation of effective mode field area of a single solid core pure silica PCF with wavelength 单实芯纯石英PCF纤芯的基模和二阶模的有效模场面积随波长的变化情况如图5所示。 从图5可看出,在波长1 550 nm处基模的有效模场面积约为54 μm2,与纤芯的面积相当,二阶模的有效模场面积约为78 μm2,比基模具有更大的模场面积,对光的约束力减小。随着波长的增加,基模和二阶模的有效模面积随之略有增加,而二阶模有效模场面积的变化相对于基模变化更为明显,这是因为波长增加时,二阶模光场更易泄露,有一部分能量扩散到空气孔包层中,导致有效模场面积增加。而由于PCF本身结构的因素,基模的光场被牢牢束缚在纤芯内传输,因此波长的变化对其的影响较小。 PCF的非线性系数通常定义为 (2) 公式中,n2为石英的非线性折射率系数,从式中可看出,γ与Aeff成反比,因此,非线性系数可以通过对模场面积的控制来调节,小模场面积的光子晶体光纤更容易实现高的非线性系数,产生非线性效应,可以用于各类非线性器件的制作;而大模场面积的PCF减小了非线性效应,由于提高模场之间的耦合效率。 图6 单实芯纯石英PCF非线性系数随波长的变化关系Fig.6 The relationship beween wavelength and nonlinear coefficient of a single solid core PCF 根据对单实芯纯石英PCF模场面积的计算结果,进一步计算了其非线性系数,n2取值为2.5×10-20m2/W。图6显示了基模和二阶模的非线性系数随波长的变化关系。从图中可看出,在不考虑材料性质的前提下,随着波长的增加,该PCF纤芯基模和二阶模的非线性系数均线性减小,在同一波长下,基模的非线性系数大于二阶模的非线性系数,在1 500~1 600 nm波长范围内,基模和二阶模的非线性系数均为10-3量级,这是由此类单实芯纯石英PCF的结构参数所决定的,较低的占空比和较大的纤芯直径,使其模场面积较大,从而减小了非线性系数。 PCF的色散包括波导色散、材料色散、折射率剖面色散、模式色散,其中后3种色散随波长的变化很小,而波导色散则会受到PCF结构的影响很大,具有灵活可变的特性。波导色散是由PCF的有效折射率决定的,可以表示为 (3) 式中,neff为PCF对应模场的有效折射率。根据前面计算结果,在1 550 nm处单实芯纯石英PCF的基模和二阶模的有效折射率分别为1.440 9和1.435 7,因此可以进一步计算出其波导色散系数。图7显示了基模和二阶模波导色散系数随波长的变化规律。 从图7中可知,在1 500~1 600 nm,随着波长的增加,单实芯纯石英PCF的基模与二阶模的波导色散系数有微小的增加,整体来看色散较为平坦,不会造成波形的明显变化,有利于信号的传输。而在同一波长下,基模的色散系数小于二阶模的色散系数,这主要是由于基模具有更加稳定的有效折射率,对光波在纤芯的束缚力较强。 本文根据有限元理论,将完美匹配层作为边界条件,利用COMSOL软件对具有5层空气孔的单实芯纯石英PCF的纤芯基模和二阶模的电场和磁场能量分布进行了仿真,并计算出其在1 550 nm处的有效折射率分别为1.440 9和1.435 7,相对于二阶模,基模的有效折射率相对更加稳定;5层空气孔结构的PCF可以减小有效模场面积和增大非线性系数;然后分别分析了单实芯纯石英PCF纤芯基模和二阶模在波长1 500~1 600 nm,基模与二阶模的波导色散系数也会随着波长的增加有微小的增加,整体来看色散较为平坦,有利于信号的传输;在同一波长下,基模的色散系数小于二阶模的色散系数,基模具有更加稳定的有效折射率。5层空气孔结构的PCF特性理论分析将为今后的光子晶体光纤实验研究发展奠定基础,该结构具有成本低廉、性能稳定等优势,可以推动PCF传感器的商用化进程,将在光纤通信、光纤传感、非线性光学等领域发挥重要作用。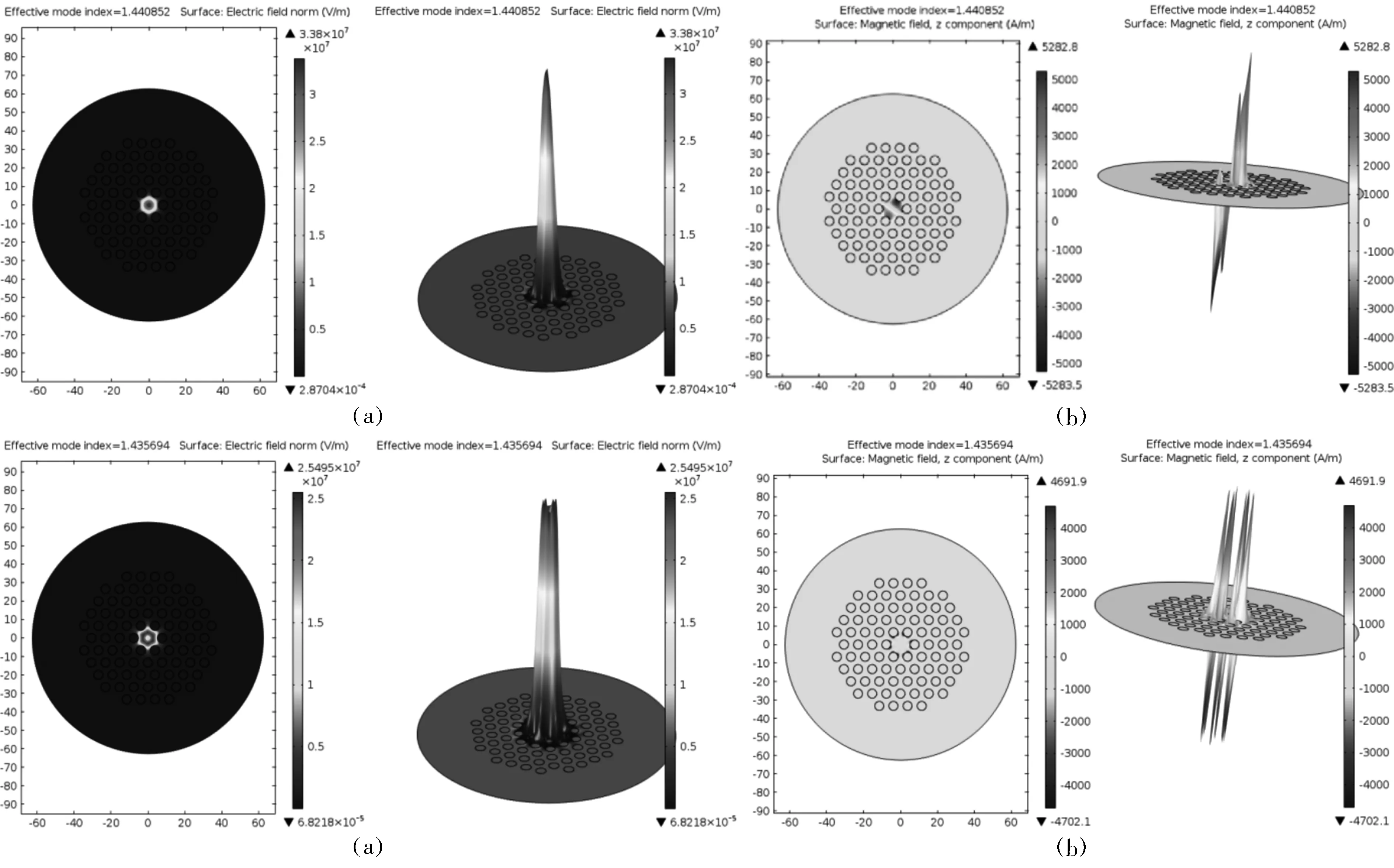
4 有效模场面积的计算
5 非线性特性分析

6 色散特性分析
7 结 论