各省经济发展情况的综合数据分析

苏忠玉, 李 玮, 李 晴, 孙 玉

(大连海洋大学 信息工程学院, 辽宁 大连 116023)

大量的高维数据在许多现代应用中变得越来越普遍,例如成像分析和数据分析。这些数据的巨大规模对计算速度和内存方面构成了巨大挑战[1-2]。分析我国各省的经济发展状况应该从多方面考察,比如该省(自治区或直辖市)的工业生产总值、固定资产投资、居民消费水平、进出口等指标。但是,由于这些指标都是对经济发展基本状况的反映,它们自身之间就存在着较强的相关性,这样在用这些指标反映经济发展状况时就造成了信息的大量重叠。这种信息的大量重叠有时甚至会抹杀经济发展状况的内在规律,所以如何能找到一组较少但却包含着较多信息量的变量,抓住主要矛盾分析数据,同时使问题得到简单化,成为了一个难题。本文提出的综合数据分析方法解决了这一难题。利用主成分分析法使用SPSS软件结合聚类分析,对31个省的经济发展状况进行了综合数据分析,该结论将为我国各省的经济发展和产业布局的科学规划提供重要的数据分析依据。

1 算 法

本文提出了一种高效的综合数据分析方法。首先,利用主成分分析法对31个省的经济发展数据进行了分析,有效减少了数据的维数和提取了主要成分。其次,采用聚类分析方法对上述主要成分进行分类,进一步降低数据量,最终获得综合分析结果。

1.1 主成分分析

主成分分析是一种多元统计方法,利用降维的思想将多个指标转化为多个综合指标,并将信息的丢失最小化。这些综合指标通常被称为主成分,生成每个主成分的转换的综合指标是原始变量中不相关变量的线性组合,具有比原始变量更好的性质。所以只使用几个主成分而不损失太多的信息,就能解决复杂的高维问题[3-9]。

算法步骤如下:

1) 规范原始数据,消除变量对量级和维数的影响;

2) 根据归一化数据矩阵计算相关系数矩阵R;

3) 求R矩阵的特征根和特征向量;

4) 确定主成分,并对主要成分的信息作出适当的解释;

5) 合成主要成分,获得综合评价值。

1.2 聚类分析

聚类是将对象划分为多个组的过程,因此同一组中的数据对象具有较高的相似性,而不同组中的数据对象则不相似。相似或不相似的定义基于属性变量的值,通常用每个对象之间的距离来表示。集群是类似的对象组集合,它们通常被视为对象[10-11]。本文采用系统聚类方法对主成分分析法获得的主成分进行深度分析。

算法步骤如下:

首先,n个样本是n个类(类别)。一个类包含一个示例。其次,2个具有最近属性的类合并到一个新类中,得到n-1个类。最后,将2个最近的类合并成n-2类,以此类推,最后,所有的样本都归为一类。

2 结 果

首先,将我国31个省的20项经济发展指标有效减少为1个主要成分;其次,根据评价结果进行综合分析将数据降为4个集群。

2.1 主成分结果

这部分是31个省20个指标的数据,原始数据来自《中国统计年鉴2012》[12]。31个省份20项指标的数据如表1所示。

2.1.1 统计检验

运用SPSS获得KMO(Kaiser-Meyer-Olkin)和巴特利特测试的结果是如表2所示。

从表2可以看出,KMO统计量=0.744>0.7,球形检验的卡方统计量=1 385.944,P=0.000<0.01,适合做主成分分析(注:KMO是相关系数与偏相关系数的一个比值,用于比较变量间简单相关系数与偏相关系数的一个统计量,其值越接近1,表明越适合做主成分分析;巴特利球形度检验是判断变量的相关系数矩阵是否为单位阵的一个统计量,其相伴概率小于显著性(0.05或0.1),表明相关系数矩阵不是单位矩阵,适合做主成分分析[13])。

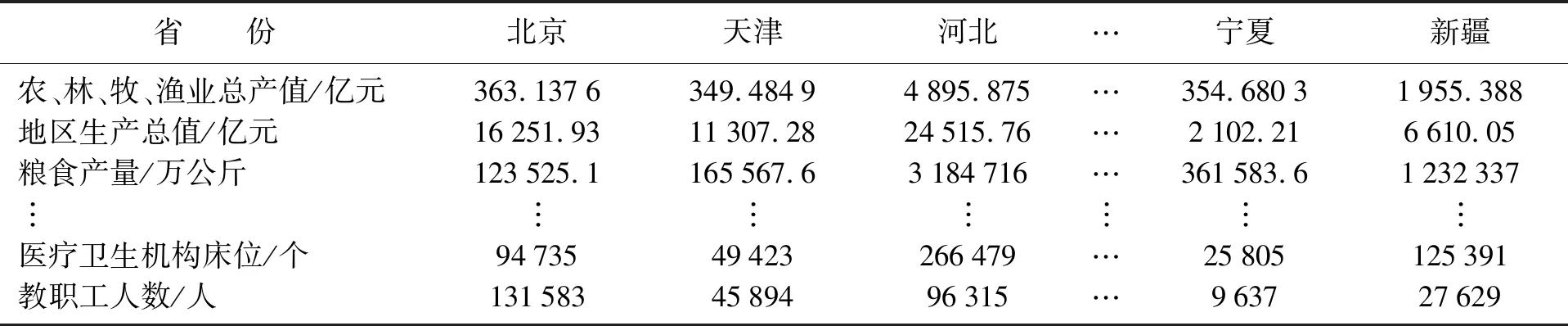
表1 经济发展状况数据Table 1 Economic development data

表2 KMO和巴特利特检验Table 2 KMO and bartlett test

2.1.2 碎石图

图1 主成分碎石图Fig.1 Principal component scree plot

2.1.3 提取因子

根据图1可知,到第2个主成分特征值出现陡峭的拐点,第1主成分特征值与其余主成分特征值呈现明显的区分,其余特征值基本接近持平。

由表3可知,第1个主成分特征值占所有信息的96.709%,占据所有信息的大部分,所以确定主成分个数为1个。这样仅用1个主成分就可以表达原来所有指标所能表达信息的绝大部分[14]。

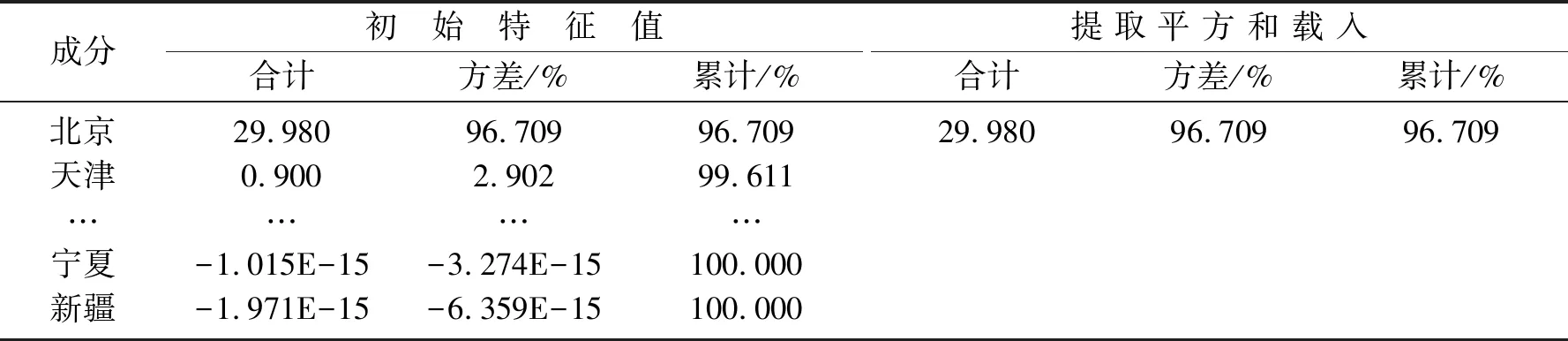
表3 总方差解释Table 3 Total variance interpretation

2.1.4 计算各成分得分

运用SPSS计算每个组件的得分矩阵,输出结果如表4所示。以各主成分在每个指标上的得分为权重,主成分的表达式为第1主成分:

表4 因子得分系数矩阵Table 4 Factor scoring coefficient matrix

2.1.5 计算各变量得分

把因子1的数值分别乘以各自的方差的算术平方根,得出主成分1的得分,见表5。

2.2 聚类分析

在主成分分析的基础上,利用SPSS软件对数据进行聚类分析。31个省的20个指标数据的1个主要组成部分的组数为4,如表6所示。

表5 经济发展状况数据的主要组成部分Table 5 The main component of data on economic development

表6 基于PCA的聚类分析Table 6 Cluster analysis based on PCA

3 结 论

本文提出一种综合数据分析方法,有效地减少了31个省的20个指标数据。通过主成分分析,将31个省的20个指标数据减少为一个主要成分。结合聚类分析,将主成分结果归纳为4类。本文获得的结论将为预测我国内地各省经济的发展情况、科学规划产业布局、优化产业结构等方面提供重要的数据分析依据。