例析三角恒等变换中的角变换

■王丽娜

三角恒等变换问题中，常见的题型有给值求角和给角求值，解答这类问题的关键是角的变换，也就是构造角的问题。角变换的核心是利用已知角构造出所求角，然后利用和差角公式展开求解。下面举例分析，供大家参考。

解：因为，所以

评析：题中所给角不是特殊角，不能用和差角公式展开求解。如果将所求角进行变换，即则问题就变得简单易解了。

例2已知则tan（β-α）的值为____。

解：β-α=（α+β）-2α。

故tan（β-α）=tan[ （α+β）-2α]

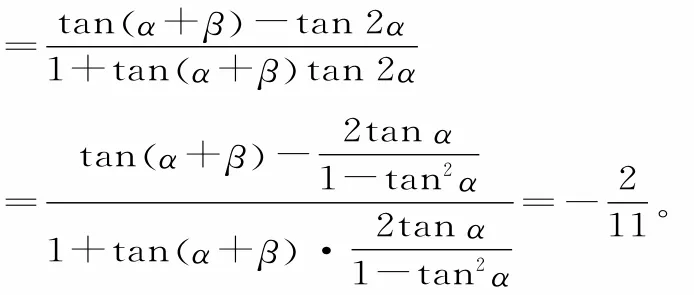
评析：把所求角进行变换，即β-α=（α+β）-2α，再借助正切的差角公式和二倍角公式求解。

例3已知，且0＜x＜，则的值为（ ）。

解：因为，所以原式=应选A。

评析：把所求角进行变换，即2x=再利用诱导公式和二倍角公式求解。

例4已知且求sin（α+β）的值。

解：由，可得由可 得

评析：解答本题的关键还是角的变换，即解题时，要注意角的取值范围对三角函数值的影响。