采用广义椭圆方程曲线导轨的径向球塞马达的输出特性
(南昌大学机电工程学院, 江西南昌 330031)
引言
液压驱动是近些年机械驱动的主要方式之一,对液压马达的扭矩、排量、噪声值等要求也越来越高[1-2]。精确获取径向液压马达定子导轨曲线是径向液压马达的核心技术之一,不同厂家生产的径向液压马达导轨曲线不同,液压马达生产厂家往往将轨曲线作为核心技术并对外保密[3-4]。目前市场上成熟且公开的等加速等减速曲线,转子运行过程中,始终存在着较大的柔性冲击问题,作为研究热点的等接触应力曲线某些性能优异, 但是曲线绘制通常采用曲线拟合的办法,形式复杂,在实际加工中达不到要求精度而未得到广泛应用[5-6]。
新型的径向马达定子导轨曲线的发现与研究是推动液压马达技术进步的核心动力之一[7],通过对椭圆曲线的观察,改变曲线的作用次数,可以得到一系列新型的径向球塞液压马达定子导轨曲线,通过理论推导与仿真来探究该类型曲线对径向球塞马达的性能影响。
1 方程曲线的来源与该曲线导轨的建模
1.1 广义椭圆方程曲线的来源
观察椭圆曲线,其曲线由2个对称的波形线构成[8],改变椭圆曲线的作用次数,可以得到3, 4, 5, 6个等数值的对称波形线,径向球塞液压马达通常需要5, 6, 8, 9个或者10个对称的波形线[9]。
获取径向球塞马达广义椭圆方程曲线(钢球运行的轨迹曲线)过程如下:
在椭圆极坐标方程中,一动点在椭圆轨迹上运动,有极径:
(1)
式中,a为椭圆短半轴;b为椭圆长半轴;θ为椭圆转角,则椭圆上任意点(x,y)有:

(2)
改变椭圆方程曲线的作用次数,得到的新型曲线可以用广义椭圆极坐标方程生成。
在广义椭圆极坐标方程中,一动点在广义椭圆轨迹上运动,有极径:
(3)
式中,a1为广义椭圆短半轴;b1为广义椭圆长半轴;θ1为广义椭圆转角;n为广义椭圆作用次数,即曲线波形线个数,当n=2时,广义椭圆极坐标方程对应标准椭圆极坐标方程。
则广义椭圆极坐标方程上任意点(x1,y1)有:
(4)
分析式(3),该方程生成的曲线是一条形式简单、连续、封闭、高次可导的周期性曲线,可解决内曲线马达内部柔性冲击问题。
1.2 该曲线导轨的建模
用MATLAB获取上述广义椭圆方程曲线数据后,将数据导入到SolidWorks绘图软件中,用半径为r的圆在其轨迹上扫描,扫描线构成的包络线进行纵向拉伸即为本研究的广义椭圆方程曲线导轨。
当取短半轴a1为100 mm,长半轴b1为108 mm,r为10 mm时,n为5, 6, 8, 9时,径向球塞马达广义椭圆方程曲线导轨如图1所示。

图1 n取不同值取得的广义椭圆方程曲线导轨
2 结构及工作原理
采用广义椭圆曲线导轨的液压马达结构如图2所示,采用了图1中n为6时的径向球塞马达广义椭圆定子曲线导轨。由图1定子曲线导轨可知,n的数值即为广义椭圆定子导轨曲线球塞马达的长、短半轴个数,即作用次数(对称的波形线个数)。在液压力的作用下,1个钢球紧贴定子内壁运行一圈的过程中,钢球每经历一次由短半轴到长半轴再到短半轴的变化,可以完成一次压、排油过程。其中压油过程(钢球从短半轴运行到长半轴),高压油通过压油腔给钢球底部提供推力,使钢球顶部挤压定子导轨内壁,定子导轨内壁对钢球的反作用力N可以分解为与球塞底部液压力相平衡的径向力F和切向力G, 切向力G乘以ρ1即为1个钢球所提供的扭矩, 所有处于压油过程的钢球产生的扭矩累加即为瞬时扭矩, 共同推动转子运动;

1.定子 2.钢球 3.球塞 4.转子 5.配流轴图2 采用广义椭圆方程曲线导轨的球塞液压马达结构
排油过程(钢球从长半轴运行到短半轴),钢球底部的低压油从排油腔排出,钢球通过惯性作用继续运转[10]。
3 方程参数对该类型马达输出扭矩的影响
由图2液压马达结构及工作过程可知,n值的增大可以增加马达的作用次数,在不计摩擦及泄漏的情况下,广义马达工作过程中输出的平均扭矩T为:
(5)
为反映长、短半轴的比值关系,引入长、短半轴比例系数K:
(6)
式中,T为平均扭矩,N·m; Δp为压油腔与排油腔的油压差,MPa;V为广义椭圆定子导轨曲线径向球塞马达排量,mL·r-1;n为广义椭圆方程曲线导轨作用次数;z为钢球个数;s为广义椭圆定子曲线导轨球塞马达钢球的行程,mm,且有s=b1-a1;r为钢球半径,mm。
分析式(5),该类型马达输出的平均扭矩T与油压差Δp、作用次数n,钢球个数z、钢球行程s和钢球半径r的二次方成正比关系。
在有限的容积中追求液压马达大扭矩的情况下,可以增大作用次数n以及长、短半轴比例系数K,但是随着数值n的增加,广义椭圆方程曲线导轨加工难度增加,在尖角(长轴)处产生过切现象的几率增加,n和K增加到一定数值时,会使液压马达因钢球“卡死”而停止工作,因此n通常取5~12的整数值,106%≤K≤114%。
4 方程参数对该类型马达压力角的影响
压力角是反映径向马达输出扭矩能力的一项参数,马达内部钢球中心的径向线与法向线的夹角即为压力角[11],如图3所示。
其中,θ1为钢球中心径向线与x轴的夹角,也是广义椭圆转角。
(7)
k1=tanθ1
(8)
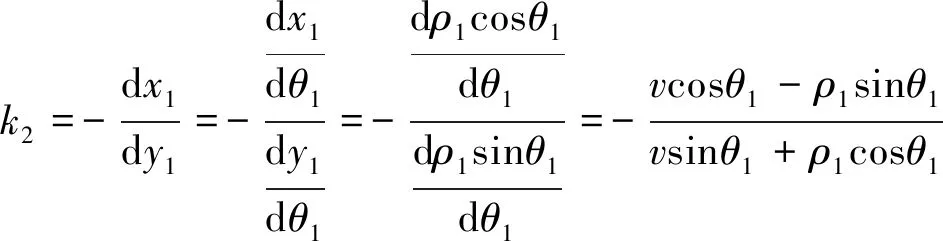
(9)

(10)
β=arctan(k)
(11)
式中,ρ1为广义椭圆极坐标方程中的极径,即钢球中心到坐标原点的距离,mm;v为钢球相对于球塞孔运动的速度,mm·rad-1;k1为钢球中心径向线斜率;k2为钢球中心法向线斜率;k为压力角斜率;β为压力角。

图3 压力角分析图
取短轴a1为100 mm,长轴b1为108 mm,n为5时,在MATLAB中运行式(7)~式(11),得到转子旋转一圈过程中压力角变化图如图4所示。

图4 五作用广义椭圆方程曲线径向马达的压力角变化图
分析图4,压力角的变化周期为T0=2π/5,压力角最大值βmax=10.90°,压力角最小值为βmin=-10.90°,压力角变化连续。分别改变b1和n的值,控制其他数值不变,继续运行上述计算式,探究该类型马达压力角的变化情况,有表1和表2。
分析表1,随着b1数值的增大,即长、短半轴比例系数的增大,压力角最大值βmax增大,压力角最小值βmin减小,始终存在βmax=βmin,压力角的变化周期为T0未发生变化,表明长、短半轴比例系数K对压力角的变化周期无影响。
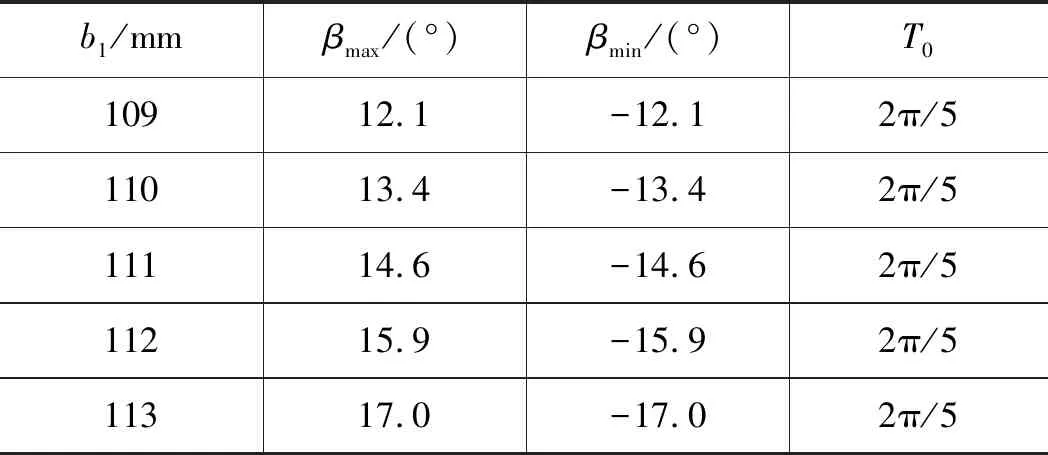
表1 b1取不同值时值压力角变化情况

表2 n取不同值时值压力角变化情况
分析表2,随着作用次数的增大,压力角最大值βmax增大,压力角最小值βmin减小,始终存在βmax=βmin,压力角的变化周期为T0=2π/n,表明压力角的变化周期T0与作用次数n成反比关系。
综合分析表1和表2,当需适当增大该类型马达的压力角时,可以适当增大长、短半轴比例系数K和作用次数n。
5 方程参数和钢球个数对该类型马达流量脉动与扭矩脉动的影响
液压马达的流量脉动率与扭矩脉动率是反映液压马达噪声情况的两项重要参数,流量脉动率与扭矩脉动率越大,液压马达工作过程中产生的噪声越大。液压马达的流量脉动率σ1、扭矩脉动率σ2计算为:
(12)
(13)
式中,qmax,qmin分别为最大瞬时流量和最小瞬时流量;q为平均流量,mL·s-1;Tmax,Tmin分别为最大瞬时扭矩和最小瞬时扭矩;T为平均扭矩,N·m; 在不计摩擦与泄漏的情况下,平均扭矩T可由式(5)计算,平均流量q的计算式为:
为计算qmax,qmin,Tmax和Tmin的数值,需计算在不同处转角处的瞬时流量q瞬时和瞬时扭矩T瞬时,其计算式为:
(15)
(16)
式中,r为钢球半径,mm;n为广义椭圆方程参数;z为钢球个数;t为马达转数,r·s-1;vi为每个钢球相对于球塞孔的速度,当vi<0时,钢球对应的球塞底部排出低压油,将vi=0代入式(15)中计算,Δp为液压马达压油腔与排油腔的油压差,MPa;V为马达排量,mL·r-1;p为钢球底部压力;ρi为各个钢球的极径;βi为各个钢球的压力角,(°)。
取短轴a1为100 mm,长轴b1为108 mm,n=5,钢球半径r=10 mm,钢球个数z=10,t=4 r·s-1,压油腔油压p1为10 MPa,排油腔油压p2为0.5 MPa时,Δp=p1-p2。当tanβi>0时,钢球底部处于压油腔,p=p1=10 MPa,当tanβi≤0时,钢球底部处于排油腔,p=p2=0.5 MPa。
在MATLAB中运行式(7)和式(15),液压马达的瞬时流量q瞬时变化情况如图5所示。
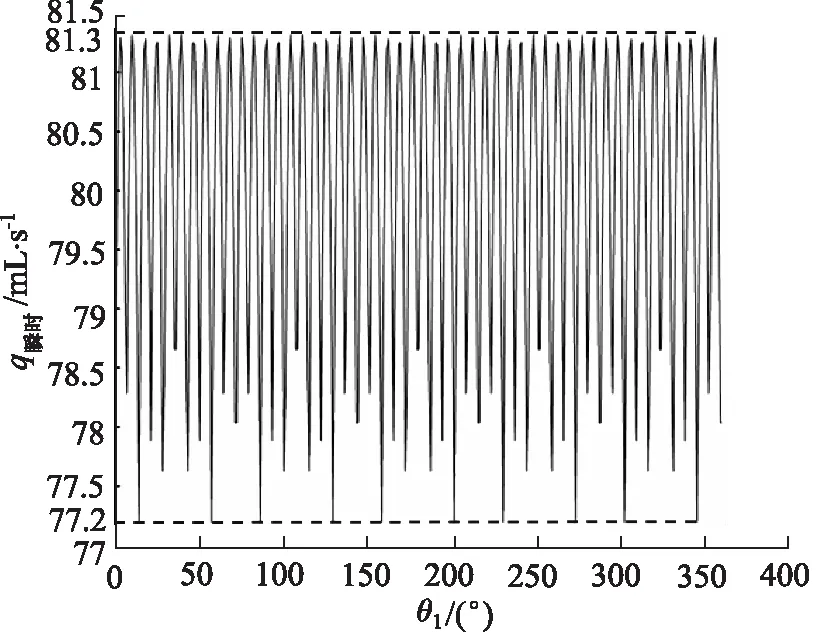
图5 广义椭圆方程曲线径向马达瞬时流量变化图
分析图5,瞬时流量变化周期T1为2π/5,最大瞬时流量qmax=81.3 mL·s-1,最小瞬时流量qmin=77.2 mL·s-1,运行式(14),有q=80 mL·s-1,再运行式(12)得σ1=5.13%。
在MATLAB中运行式(3)、式(7)~(11)和式(16),液压马达的瞬T瞬时时扭矩变化情况如图6所示。

图6 广义椭圆方程曲线径向马达瞬时扭矩变化图
分析图6,瞬时扭矩变化周期T2为2π/5,最大瞬时扭矩Tmax=193.2 N·m,最小瞬时扭矩Tmin=183.1 N·m,运行式(5),有T=190 N·m,再运行式(13)得σ2=5.32%。
分别改变长轴b1、作用次数n和钢球个数z,控制其他数值不变,继续运行上述计算式,探究该类型马达流量脉动与扭矩脉动的变化情况,有表3~表5。

表3 b1取不同值时该类型马达流量脉动与扭矩脉动的变化情况

表4 n取不同值时该类型马达流量脉动与扭矩脉动的变化情况

表5 z取不同值时该类型马达流量脉动与扭矩脉动的变化情况
分析表3,b1发生改变时,流量脉动率σ1、瞬时流量变化周期T1、扭矩脉动率σ2、瞬时扭矩变化周期T2数值均不变,表明长、短半轴比例系数K对该类型马达流量脉动和扭矩脉动无影响。
分析表4,当作用次数n为大于5的奇数时,随着作用次数n的增加,该类型马达流量脉动σ1变小,当作用次数n为偶数时,随着作用次数n的增加,该类型马达流量脉动σ1变大,作用次数n对该类型马达扭矩脉动率σ2影响甚微,瞬时流量变化周期T1、瞬时扭矩变化周期T2均为2π/n,表明瞬时流量变化周期T1、瞬时扭矩变化周期T2与作用次数n成反比关系。
分析表5,钢球个数z为奇数时,随着钢球个数z的增加,该类型马达流量脉动σ1和扭矩脉动率σ2变小,作用次数为奇数的该类型马达流量脉动σ1比作用次数为该奇数相邻的两个偶数的该类型马达流量脉动σ1小,钢球个数为8时,该类型马达流量脉动σ1和扭矩脉动率σ2均出现极大值,钢球个数z发生改变时,瞬时流量变化周期T1、瞬时扭矩变化周期T2均不发生变化,表明瞬时流量变化周期T1、瞬时扭矩变化周期T2与钢球个数无关。
综合分析表3~表5,当需取制作低噪声的马达,作用次数n和钢球个数z均应选择数值较大的奇数。当作用次数n=5,钢球个数z=9时,该类型马达流量脉动σ1=0.89%,扭矩脉动率σ2=1.57%,趋近于恒流、恒扭矩,液压马达的流量脉动与扭矩脉动是造成液压噪声根源,流量脉动率和扭矩脉动率越大,噪声越大,流量脉动率和扭矩脉动率越小,噪声越小,此外广义椭圆方程曲线可解决内曲线马达内部冲击问题,说明广义椭圆方程曲线导轨在制作低噪声的径向液压马达方面有着显著的优异性能。
6 结论
(1) 长、短半轴比例系数对该类型的径向球塞马达流量脉动和扭矩脉动无影响;
(2) 当作用次数为偶数时,随着作用次数的增加,该类型马达流量脉动变大,作用次数对该类型马达扭矩脉动率影响甚微;
(3) 钢球个数为奇数时,随着钢球个数的增加,该类型马达流量脉动率和扭矩脉动率变小,作用次数为奇数的该类型马达流量脉动率比作用次数为该奇数相邻的两个偶数的该类型马达流量脉动小;
(4) 当需制取大扭矩的径向液压马达时,马达的作用次数和长、短轴比例系数宜选择较大的数值;当需制取低噪声的径向液压球塞马达时,马达的作用次数与马达内部的钢球个数宜选择较大的奇数;
(5) 广义椭圆方程曲线导轨在制作低噪声的径向液压马达方面有着显著的优异性能,为设计和开发新型的低噪声径向液压马达提供了理论依据。

