阀控缸系统有限时间滑模控制
(北京交通大学机械与电子控制工程学院, 北京 100044)
引言
液压伺服系统具有响应快、精度高等优点,广泛应用于机械制造、船舶操纵和工业过程控制中。而在控制系统研究中,稳定性是控制系统研究中的一个重要环节。在阀控缸系统的研究中,控制方法均为无限时间稳定,而对于控制系统,收敛性能是控制系统中的关键指标,从时间优化的角度实现有限时间控制才是最优控制[1-2]。
俞珏等[3]针对阀控缸系统的强非线性提出了一种反馈线性化控制器。王迪[4]以阀控液压缸系统为研究对象,基于不同负载工况提出了自抗扰控制算法。林浩等[5]针对电液伺服系统中非线性和参数不确定的问题,提出了一种自适应Backstepping控制方法。冯亚恒[6]针对阀控缸系统在参数波动较大时PID控制效果变差的问题提出了一种鲁棒H∞混合灵敏度控制算法,通过仿真验证控制效果优于PID控制。但是以上所提出控制算法均为渐近稳定,在收敛时间上为无限时间收敛。
由于滑模控制具有响应速度快、对参数及扰动变化不灵敏和物理实现简单等特点,越来越多的被应用在液压控制领域[7-8]。在传统的滑模变结构控制中,滑模面为线性滑模面,系统到达滑模面后,跟踪误差渐近收敛至0,通过选择滑动模态参数来调整渐近收敛的速度。在液压控制领域中,各种滑模变结构控制方法被提出,提高了液压控制系统的控制性能,推动和发展了滑模变结构控制在液压系统中的应用[9-10]。然而,无论如何调整滑模参数,系统状态跟踪误差都不会在有时间内收敛至0。为了解决无限时间收敛的问题获得更好的性能,Terminal滑模控制策略被提出并受到学者广泛关注。

1 阀控缸系统数学模型
1.1 阀控缸系统描述
阀控缸系统按输出信号可分为位置控制系统、速度控制系统、加速度控制系统、压力控制系统等,在工程应用中阀控缸系统的位置控制尤为重要。然而,在阀控缸系统位置控制中又分为阀控对称缸与阀控非对称缸2种。由于阀控对称缸具有一定普适性,因此选取阀控对称缸为建模对象。
在分析阀控缸系统的特性之前需对系统进行数学建模。为了便于物理模型的数学公式推导,借鉴前人在阀控液压缸建模过程中考虑或者忽略的因素,在一些条件理想情况下,建立阀控缸模型[13],系统原理图如图1所示。
以图1所示阀控缸系统为研究对象,分别建立阀的流量方程、流量连续性方程和力平衡方程。
1) 阀的流量方程
QL=Kqxv-KcpL
(1)
式中,Kq—— 阀在稳态工作点附近的流量增益
xv—— 阀芯位移
Kc—— 稳态工作点附近流量-压力系数
pL—— 负载压降

图1 电液伺服系统原理图
2) 液压缸连续性方程
(2)
式中,A—— 活塞的有效面积
y—— 活塞位移
Cte—— 总泄漏系数
βe—— 油液弹性模数
Vt—— 2个油腔的总容积
3) 液压缸与负载的力平衡方程
不考虑库伦摩擦等非线性负载并且忽略油液的质量,液压缸与负载的力平衡方程:
(3)
式中,Fg—— 液压缸产生的驱动力
m—— 活塞负载的总质量
Bc—— 活塞负载的黏性阻尼系数
K—— 负载的弹簧刚度
F—— 作用在活塞上的任意外负载力
通过式(1)~式(3)即可得到阀控缸系统数学模型。
1.2 阀控缸系统建模
在阀控液压缸系统作为位置控制的输出元件时,一般没有弹性负载,因此K=0[14]。由于伺服阀和液压缸的泄漏产生的阻尼系数一般大于活塞负载的黏性阻尼系数Bc,所以Bc(Kc+Cte)/A2≤1,可以忽略,因此数学模型可以简化为:
(4)
选取状态变量[15]:
(5)
在不考虑外界干扰的情况下,状态方程为:
(6)
其中,
Kce=Kc+Cte
式中,ωh—— 液压缸固有频率
ζh—— 液压阻尼比
Kce—— 总的流量-压力系数
存在干扰的情况下,系统状态方程为:
(7)
其中,
u=xv
式中,u—— 控制器输入
βe—— 体积弹性模量
d(t) —— 外界干扰
2 有限时间控制器设计
2.1 有限时间滑模面设计
对阀控缸系统进行位置伺服中采用一种新型的全局快速终端滑模控制的方法。定义误差向量为:
(8)
式中,e为跟踪误差,滑模面设计为:
s=C(E-P)
(9)
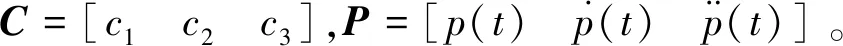
终端函数向量P(t)的构造是实现系统状态在时间T内进行跟踪的关键。终端函数向量P(t)需要满足以下三个条件:
(1) 在t=0时,s=0即E(0)=P(0);

(3)P(t)存在一阶微分并且有界。
(10)
由于阀控缸系统模型为三阶,所以n=3,因此p(t)可写为:
(11)

(12)
2.2 有限时间控制器设计

根据阀控缸模型的状态方程可得控制律为:
(14)
控制器设计为:
(15)
选择Lyapunov函数为:
(16)
对时间t求微分,由控制率式(15)以及式(9)和式(14)可得:

=-c3ηssgn(s)
=-c3ηs
(17)

3 MATLAB仿真与分析
3.1 惯性负载下MATLAB仿真
由于在t=0时,E(0)=P(0),可以看出系统在初始状态时已在滑模面上,消除了到达阶段,保证了系统的鲁棒性和稳定性。为了测试所提出的终端滑模控制策略并研究与图1中阀控系统控制相关的基本问题,运用MATLAB进行仿真,相关参数如表1所示。
分别选取参考函数xd=sint,xd=sin2πt,xd=5sint+sin2πt+sinπt/6以及xd=cost对系统及其控制方法进行仿真研究。设定初始条件为X0=[0.5,0,0]T,在不考虑外界干扰的情况下选取η=0.1。对阀控缸系统进行位置跟踪,得到仿真结果。
由图2、图3可以看出,本研究设计的控制器不仅解决了阀控缸系统中位置跟踪的非有限时间收敛到0
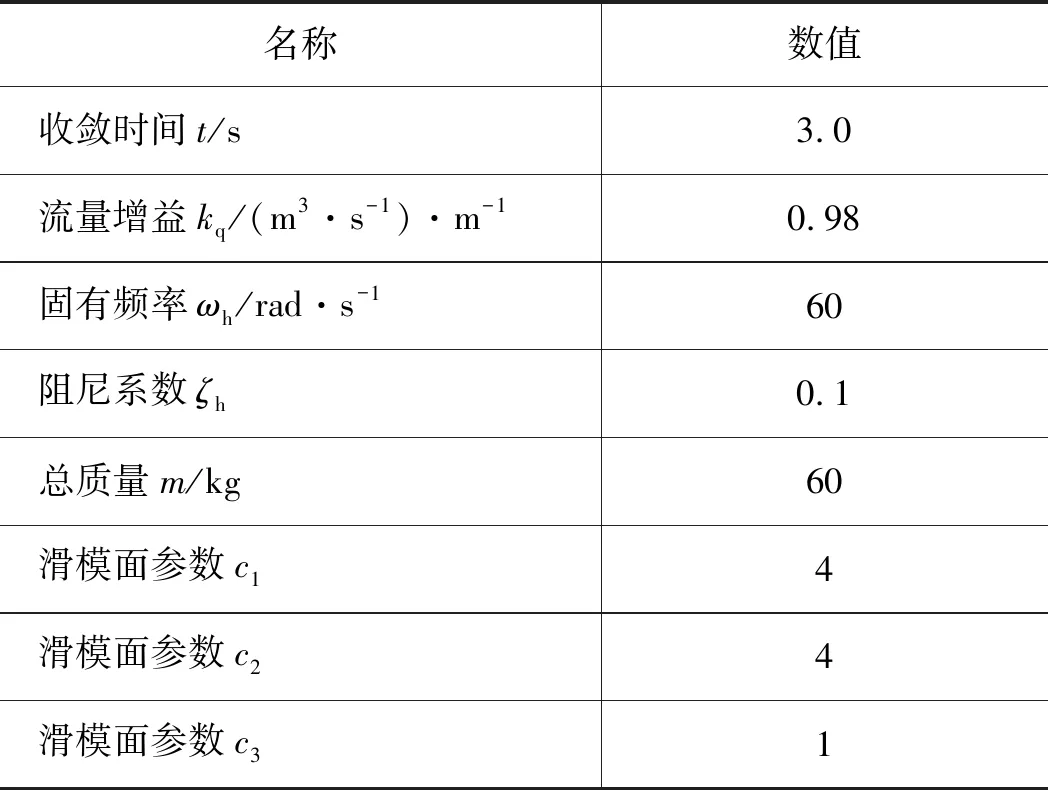
表1 模型参数
问题, 还实现了零误差跟踪。 实际信号将在所设定收敛时间T=3 s时稳定。 通过图2与图3对比可以看出,在参考信号频率增大时, 3.0 s之前会出现较大超调,但是控制器跟踪性能不受影响。

图2 xd=sint时阀控缸位置跟踪及跟踪误差曲线
当参考信号xd=5sint+sin2πt+sinπ/6t时,位置跟踪轨迹与跟踪误差如图4所示。本研究所设计控制器可实现对不同频率信号的跟踪。在收敛时间3.0 s之前,跟踪误差随参考信号频率的增加而增加。
通过图2~图5可以看出,此控制方法不仅适用于参考信号为正弦信号时,同时也适用于余弦信号。当参考信号为余弦信号时,在未完全收敛之前,系统位置跟踪误差较小,鲁棒性较强。

图3 xd=sin2πt阀控缸位置跟踪及跟踪误差曲线

图4 xd=5sint+sin2πt+sinπt/6的阀控缸位置跟踪曲线及跟踪误差曲线
3.2 存在外界干扰情况下系统仿真
在存在外界干扰的情况下,采用控制律(15),假设外界干扰d(t)是一个有界函数,即d(t)≤D。取η=50并用饱和函数替代符号函数对系统及控制器进行MATLAB仿真。分别选取参考信号xd=sint,xd=cost。
在存在外界干扰且参考信号为和时,MATLAB仿真结果如图6和图7所示。由图可以看出,期望轨迹与实际轨迹并未完全重合,但都是有界的并且跟踪误差控制在一个很小的范围内。

图5 xd=cost的阀控缸位置跟踪及跟踪误差曲线

图6 xd=sint时阀控缸位置跟踪及跟踪误差曲线
通过图8比较传统滑模控制的跟踪控制效果和终端滑模控制位置跟踪误差曲线,可以看出传统的滑模控制可实现位置跟踪渐近收敛,并且误差较大。对于终端滑模控制,液压缸伸出杆位置跟踪误差可实现在有限时间内收敛,跟踪误差控制在一个小范围内。
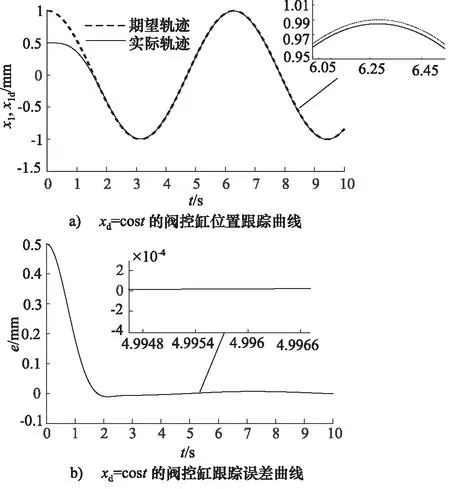
图7 xd=cost的阀控缸位置跟踪及跟踪误差曲线
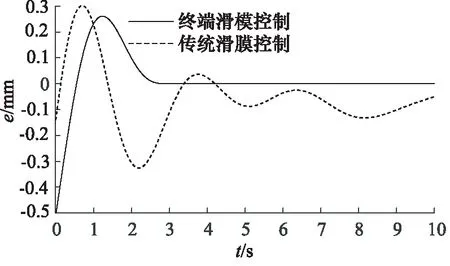
图8 xd=sint终端滑模与传统滑模跟踪误差曲线
4 结论
建立了有无外界干扰情况下阀控缸系统模型,并基于控制系统的滑模控制方法对系统进行稳态分析提出了一种终端滑模控制方法可实现位置跟踪在有限时间内完全收敛。由于在液压系统中,正弦信号和基于正弦信号的衍生信号常被应用于对产品的测试中。最终应用阀控缸系统模型对控制方法进行MATLAB仿真,得出以下结论。
(1) 通过设计终端函数使得系统初始状态位于滑模面上,消除了达到阶段,保证了系统的全局鲁棒性和稳定性;
(2) 终端滑模控制方法的控制结构及控制率具有普适性,可应用于高阶系统,并且收敛时间可根据系统规格设定;
(3) 仿真结果表明,在位置参考信号为正弦信号时可获得良好的收敛性能。终端滑模控制策略可以有效解决此类型参考信号的轨迹跟踪问题,并表现出良好鲁棒性和抗干扰性能。

