多径效应对机载干涉仪天线的影响及措施分析

安玉元, 贾朝文, 刘 翔, 胡留春

(中国电子科技集团公司第二十九研究所，四川 成都 610036)

0 引言

干涉仪测向技术[1]由于具有较高的测向精度及鲁棒性，广泛应用于机载无源测向系统，如美国的AN/APR-48A、AN/ALQ-125、ZS-2000和以色列的RAS-2“猫头鹰”等系统[2]。和比幅测向体制不同，四象限全向干涉仪测向技术利用天线单元之间相位差信息、各象限天线幅度信息，利用干涉仪测向解模糊算法[3-4]、选阵算法计算信号的方位。天线通道的幅度和相位特性对测向具有较大影响。首先，由于天线加工的不一致性，导致天线通道间的相位不一致，尤其是宽带天线，结构、加工细微的差别都可能导致相位差别很大。其次，装机后天线和天线罩之间，以及天线和机体之间存在较强耦合，对通道的幅度特性和通道间的相位特性影响较大。最后，天线与天线接口单元直接互联的射频电缆，在设计和制造上力求电长度一致，但由于技术水平限制等，实际上多路射频电缆的电长度不尽相同，从而引入了幅度和相位不一致性。因此在进行干涉仪测向之前，通常需要对天线进行幅度和相位校准。

对装机后的天线进行幅度和相位校准最好是在大型微波暗室的远场中进行，但是在通常情况下，装机后很难有足够大型的微波暗室对天线的幅度和相位差进行校准，更多情况是在开放环境(如水泥地面)完成校准工作。这种开放环境存在多径效应，会对校准的幅度和相位差产生污染，影响校准效果。本文分析了多径效应对干涉仪阵列天线通道幅度和通道间相位差的影响，并且和实验结果进行了对比，分析表明在反射点位置放置吸波材料可有效降低多径效应的影响。

1 相位干涉仪误差校准原理

图1所示为相位干涉仪测向示意图，辐射源从远场入射到天线阵口面，和天线视轴夹角为θ。由于到达每一个天线单元的距离不同，导致天线单元之间的相位存在差值。从图1不难看出，天线单元1和2之间的相位差为φ=2πdsinθ/λ，通过测量通道之间的相位差φ不难计算出信号的入射方向θ=arcsin(λφ/(2πd))(假设不存在相位模糊)。

图1 干涉仪测向几何示意图

相位差的提取精度直接关系到系统的测向精度。相位误差来源可分为两部分：一部分误差是接收机内部通道间的相位差Δφ1；另一部分误差为天线到接收机口面的误差Δφ2，这一部分误差主要来源为天线单元之间、天线与天线罩之间的耦合，以及天线到接收机口面的电缆电长度差。相对于Δφ1，Δφ2为固定系统误差，可以利用测试手段提取该误差，并加载到系统中，在实际使用时将该误差扣除。以某天线阵为例，在测向前先在视轴方向辐射信号，通过提取整个通道间的相位差扣除Δφ1得到Δφ2，在正式测向时通过扣除Δφ1和Δφ2得到由角度引起的相位差。实测Δφ2变化较大，需要在测向过程中予以扣除。

2 多路径校准精度的影响分析

提取Δφ2的过程如果是在地面开阔环境进行，此时不能不考虑地面环境等因素造成的影响，其中多径效应影响最大，下面分析多径效应对校准的影响。

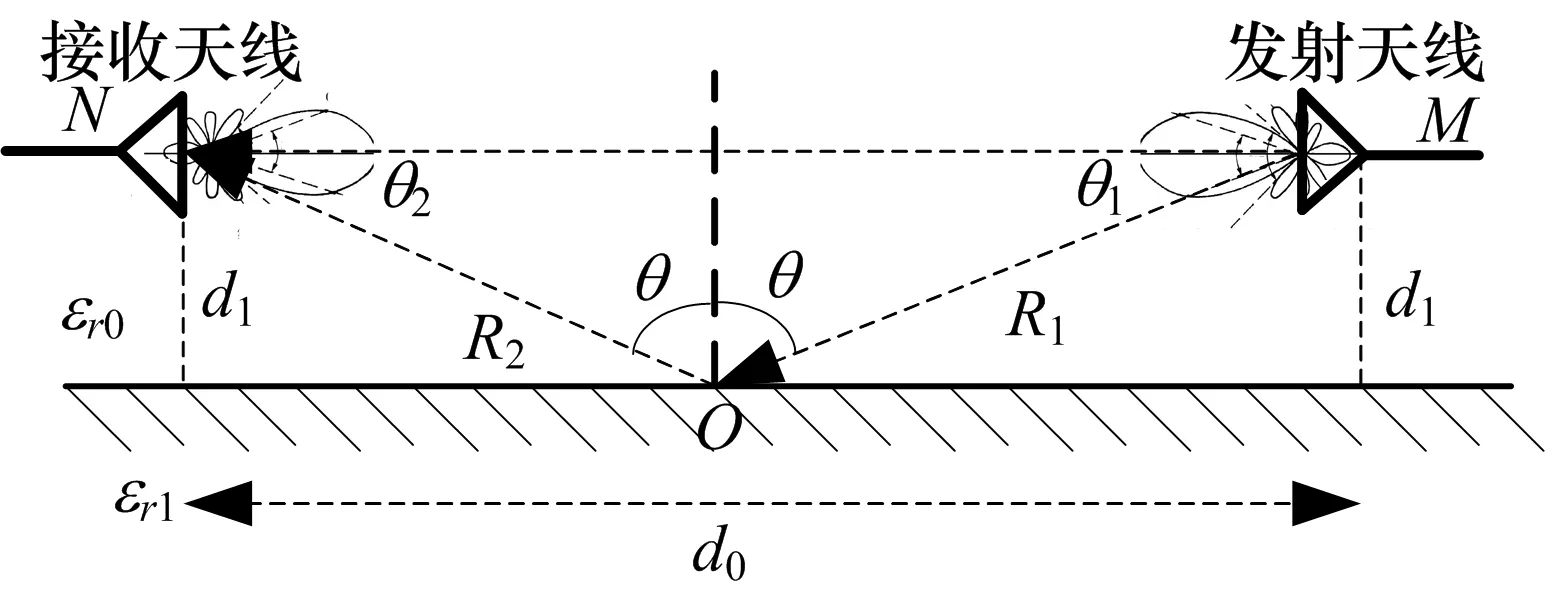
图2 多径效应示意图

图2所示为多径效应示意图，发射天线和接收天线直线距离为d0，离地面距离都为d1，空气和地面的相对介电常数分别为εr0、εr1，O点为发射天线M和接收天线N之间多径传输的反射点，即在O点满足发射信号入射角等于反射角。N点的接收天线接收从M点直接传输的信号可表示为：

Sr1=ae-jkd0/d0

(1)

式中，a表示信号幅度，k表示波数。由于多径效应的存在，N点同时还收到从M点经O点反射传到N点的信号，表示为：

Sr2=aGt(θ1)Gr(θ2)Γ(θ)e-jk(R1+R2)/(R1+R2)

(2)

式中，Gt(θ1)和Gr(θ2)分别表示发射天线和接收天线在对应角度上相对于两天线连线方向上的归一化增益。Γ(θ)表示在O点信号的反射系数，垂直极化反射系数和水平极化反射系数表示为：

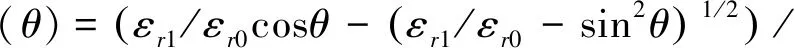
(3)

式中，Γ⊥、Γ∥分别表示反射点处垂直和水平极化波反射系数。为方便分析，这里分析垂直极化情况，水平极化分析类似。

N点接收到的信号可表示为直接到达信号Sr1和经过地面O点反射信号Sr2的复数和，即：

Sr=Sr1+Sr2

(4)

图3、图4分别给出了在θ=30°时不同路面多径效应对信号Sr相位和幅度影响，从图中可以看出，多径效应对信号的相位和幅度影响很大。图中草地、水泥地、沥青路面的复相对介电常数分别为12-3.5j、6.4-2j、3-j。

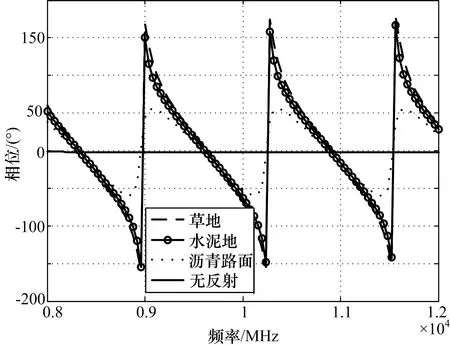
图3 不同环境下多径效应对信号相位影响

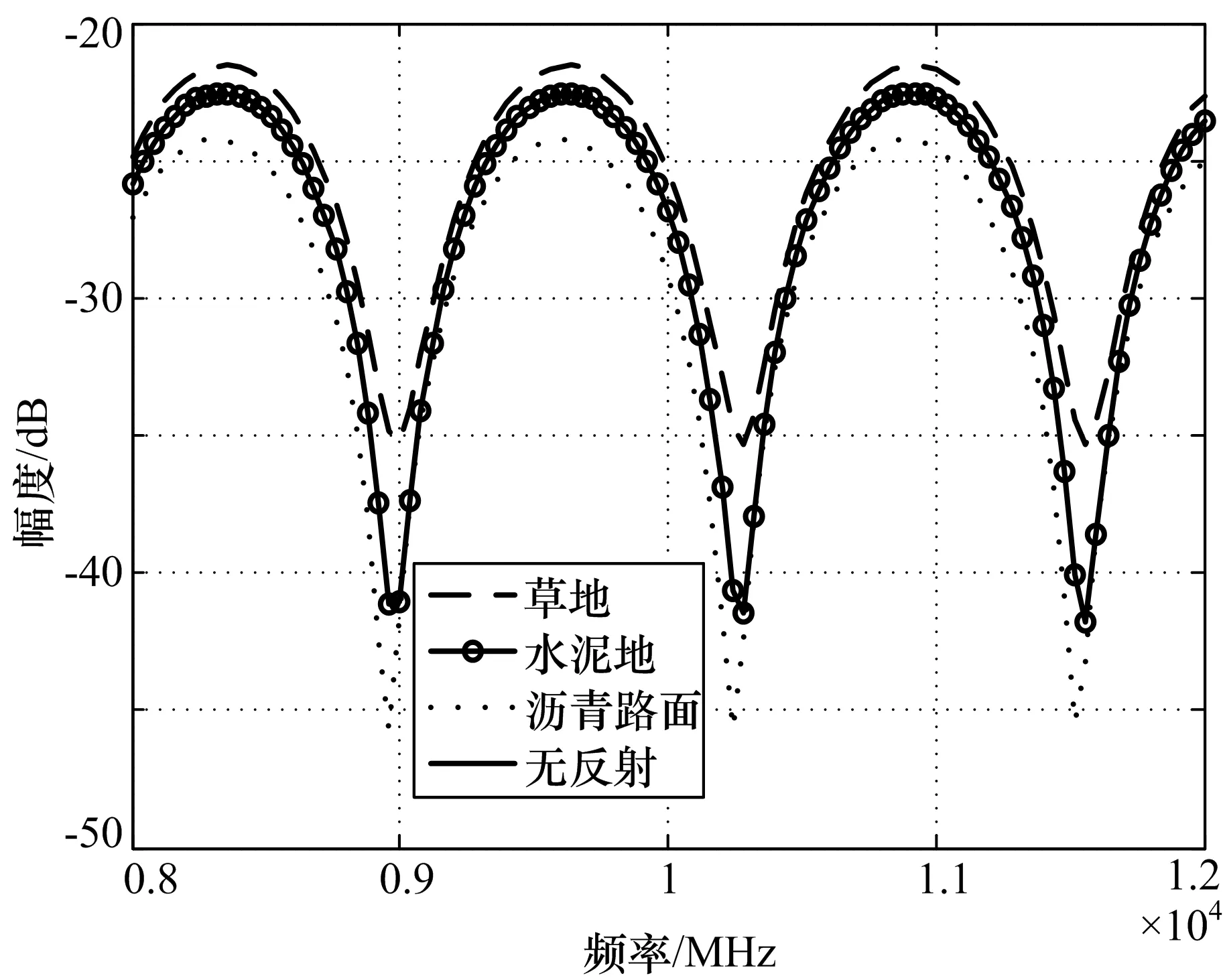
图4 不同环境下多径效应对信号幅度影响

为了验证地面反射信号Sr2对合成后的信号Sr的影响，在地面反射比较大的区域放置吸波材料，如图5所示。

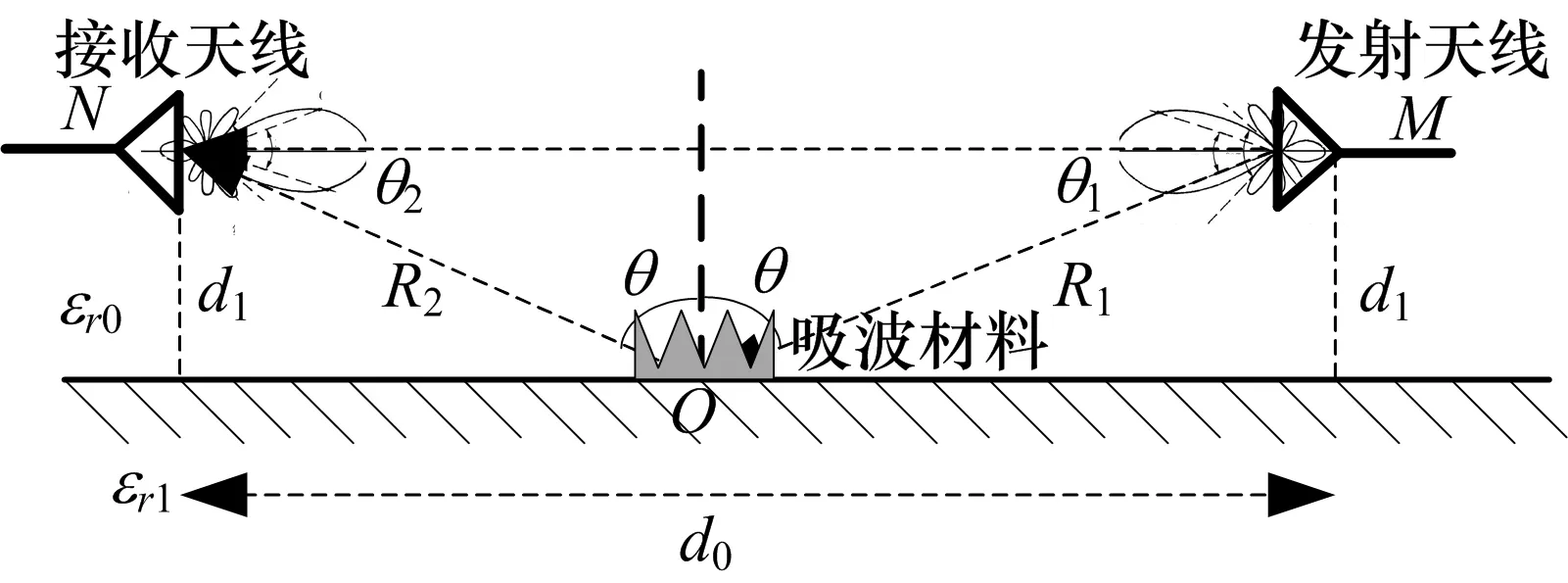
图5 地面放置吸波材料信号传播示意图

3 仿真及实验验证

3.1 天线增益测试

测试场景如图6所示，d0=30 m，d1= 1.83 m，通过计算得到θ1=θ2=7°。通过测试得7°的天线归一化增益(相对于天线视轴方向)如图7所示。

图6 多径效应测试场景

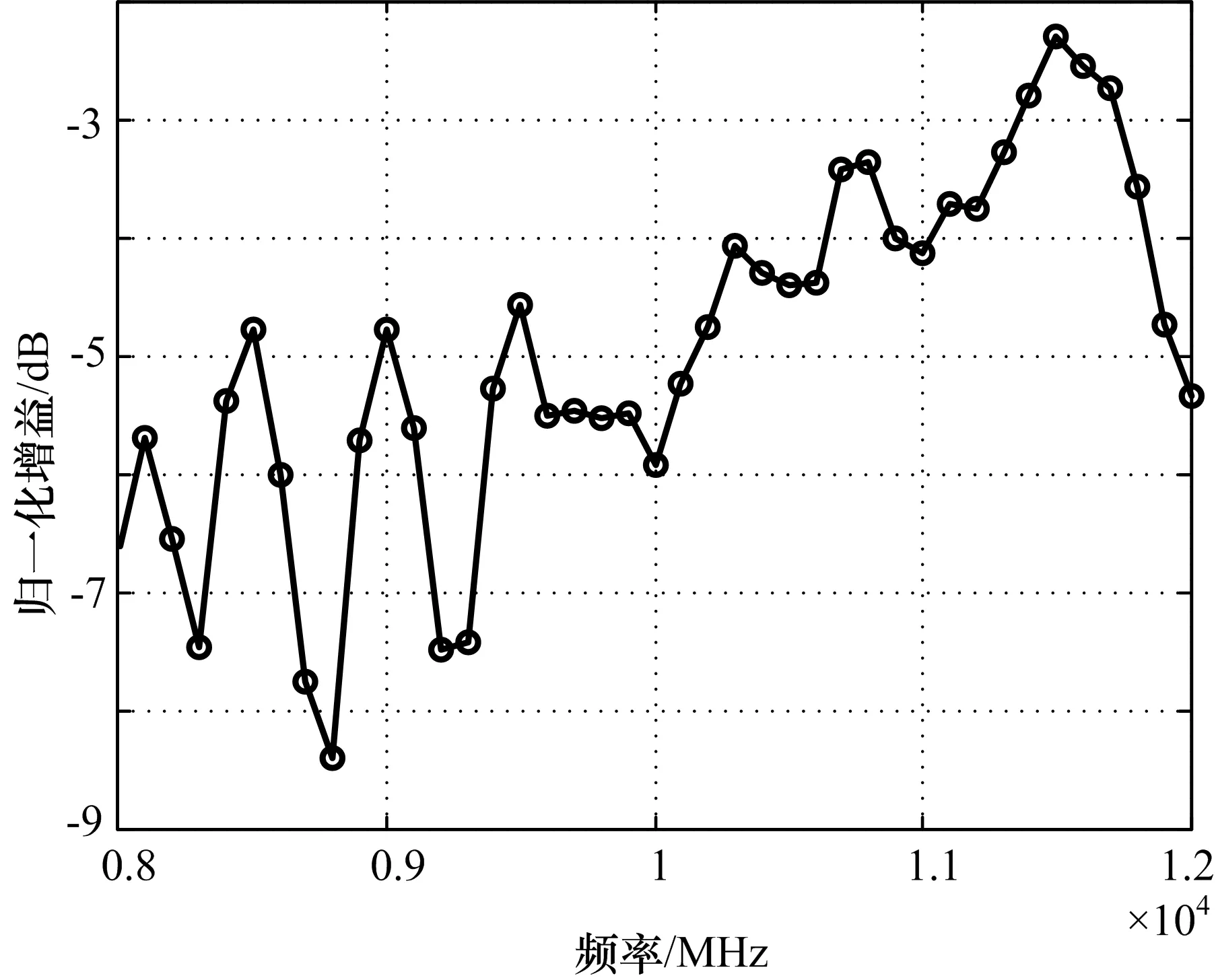
图7 多径方向天线归一化增益(相对于视轴方向)

3.2 多径效应仿真及测试

实验参数：d0=30 m，d1=1.83 m，混凝土地面εr1=6.4-2j，经过计算不难得知θ1=θ2=7°，Γ=-0.9053+0.016j。从图2可知，主要反射区在距离发射天线和接收天线连线中点处，即距离发射天线15m。分别测量没有放置吸波材料和放置吸波材料两种情况下接收天线的接收功率，两者之差即体现多径的影响，如图8所示。

图8 多径效应测试和理论仿真对比

从图8可以看出，仿真数据和实测数据吻合较好，说明仿真等效模型可信。下面通过仿真分析多径效应对通道幅度及通道间相位差影响。

3.3 多径效应对通道间相位差影响分析

仿真场景如图9所示，其中接收天线换为在垂直面上排列的4个天线单元，其他参数和3.1、3.2节一致。为分析多径效应对接收天线通道间相位差的影响，分别计算AB、AC、AD通道间相位差，以AB相位差为例。利用公式(1)和(2)可分别计算A通道无/有多径效应影响时接收信号的相位，分别表示为φA1、φA2，同理可得到B通道接收信号相位，分别表示为φB1、φB2。无/有多径相位AB通道相位差分别表示为：

φAB1=φB1-φA1

(5)

φAB2=φB2-φA2

(6)

多径效应对幅度和相位差影响如图10～13所示。图11～13还给出了无多径效应和铺设吸波材料相位差，其中吸波材料衰减按照30 dB计算，无多径效应对应不存在地面反射的场景，即根据公式(5)计算得到的通道间相位差。可以看出，由于存在多径效应，通道幅度呈驻波状波段，且频率越高，波动越大。通道间相位差波动最大达到40°左右，而铺设吸波材料后最大相位波动在±1°以内，如果在外辐射校准时不排多径影响，将直接影响干涉仪测向精度。以本仿真场景分析，当真实信号和视轴夹角为30°，频率为12 GHz时，40°的校准误差将产生0.92°的测向误差，而铺设吸波材料后，可以将这部分误差对测向精度的影响降低至0.023°。因此为了减少多径效应对外辐射校准时天线单元幅度和通道间相位差的影响，建议在反射较强的区域铺设吸波材料。

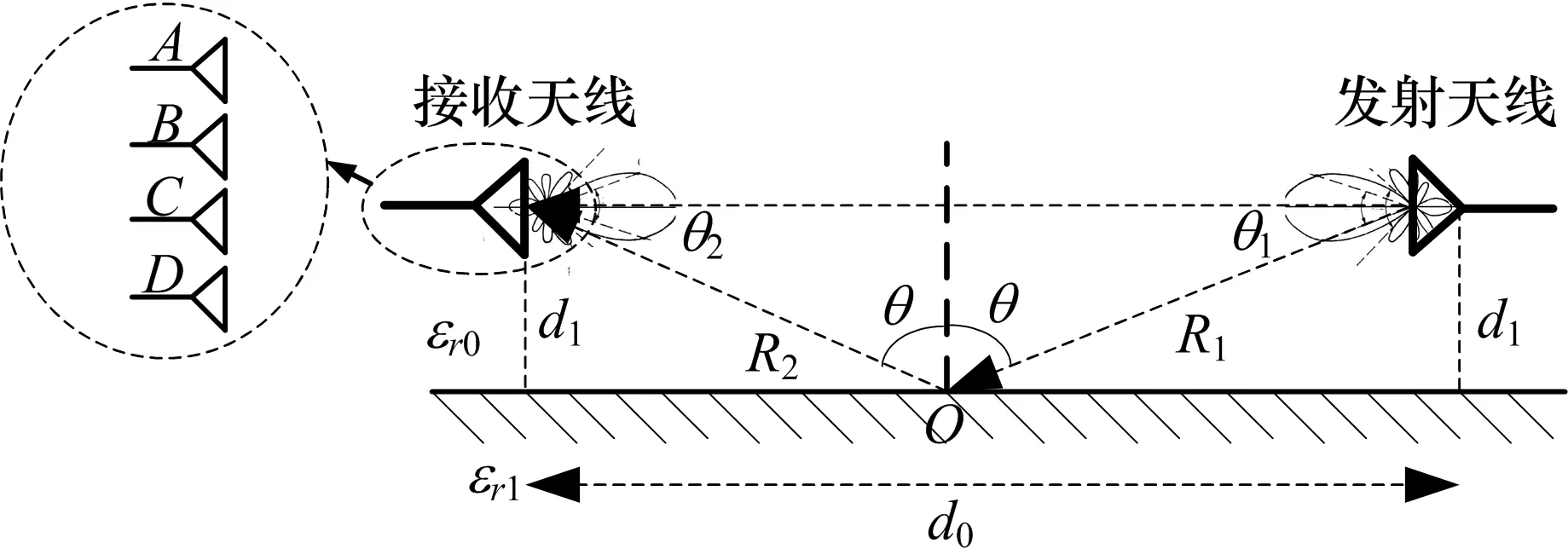
图9 多径效应对通道相位差影响仿真场景

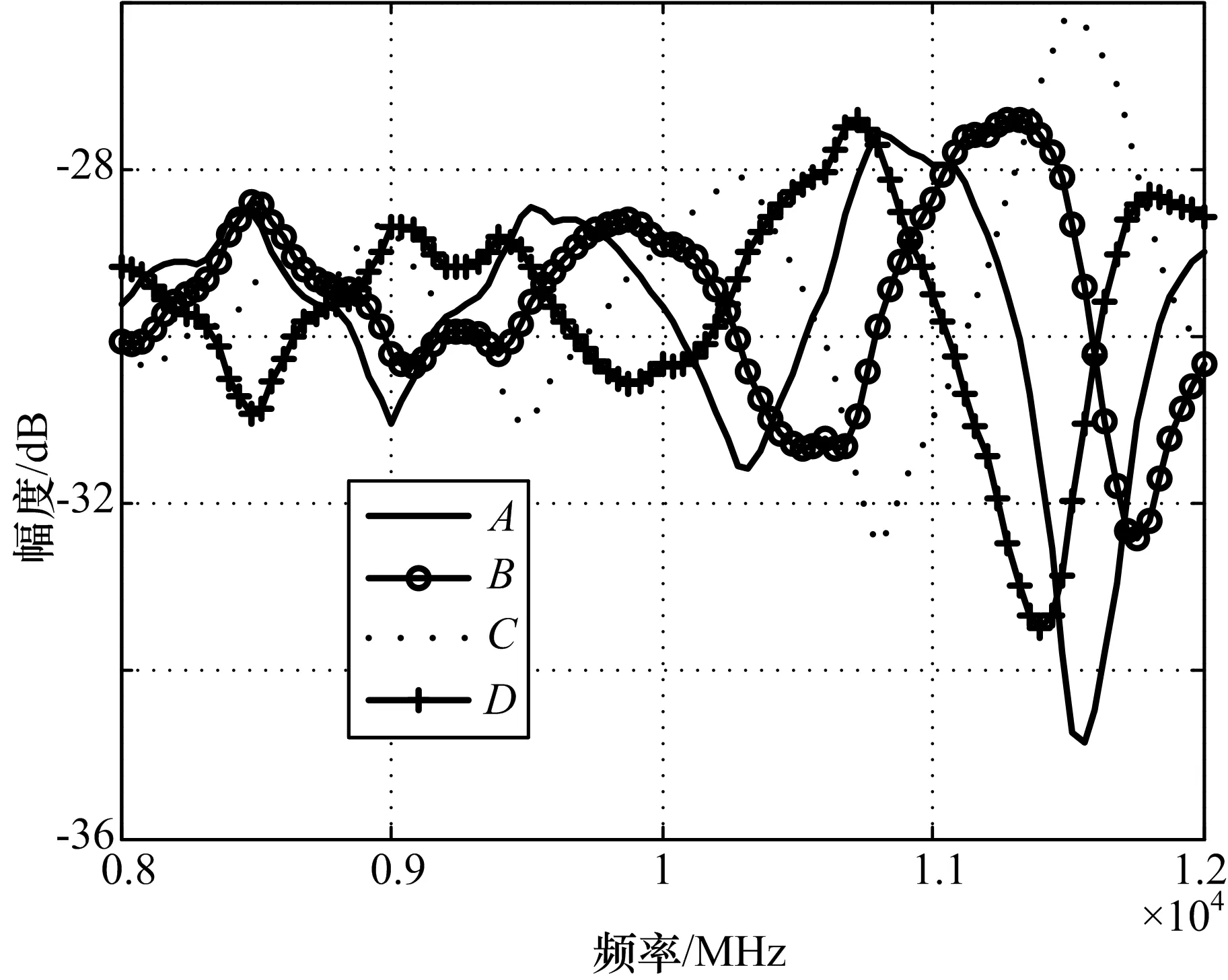
图10 多径效应对通道幅度影响

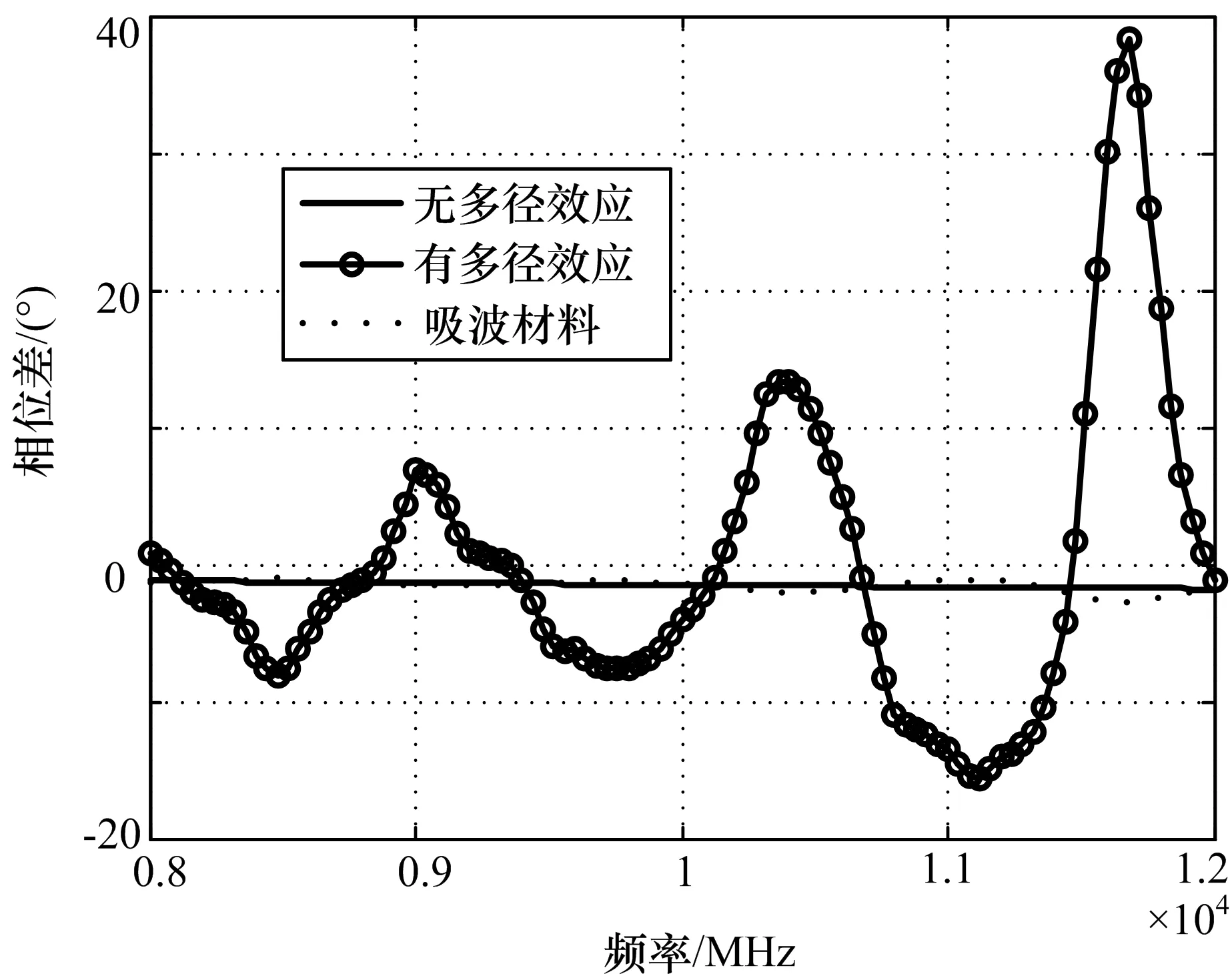
图11 多径效应对AB通道相位差影响

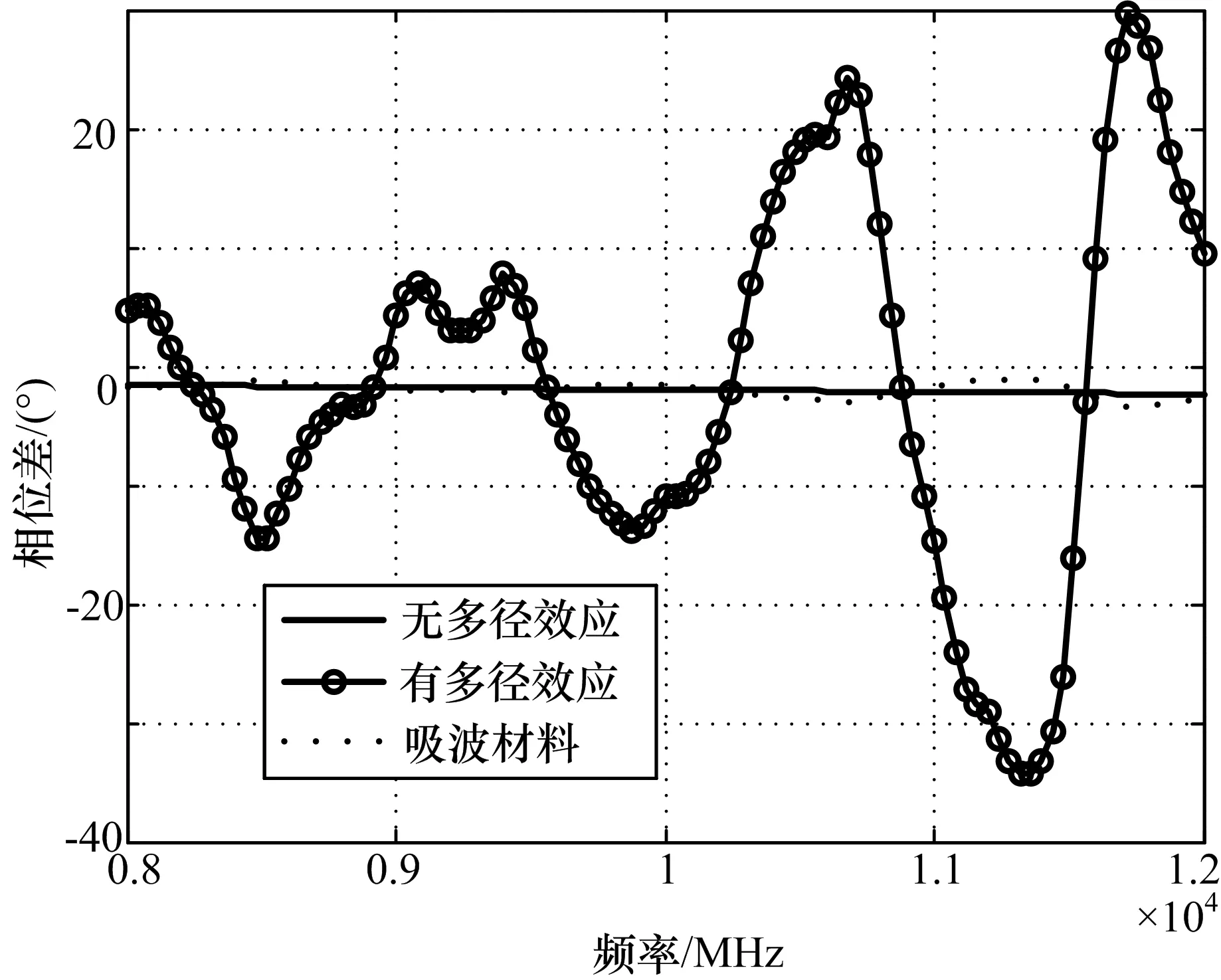
图12 多径效应对AC通道相位差影响

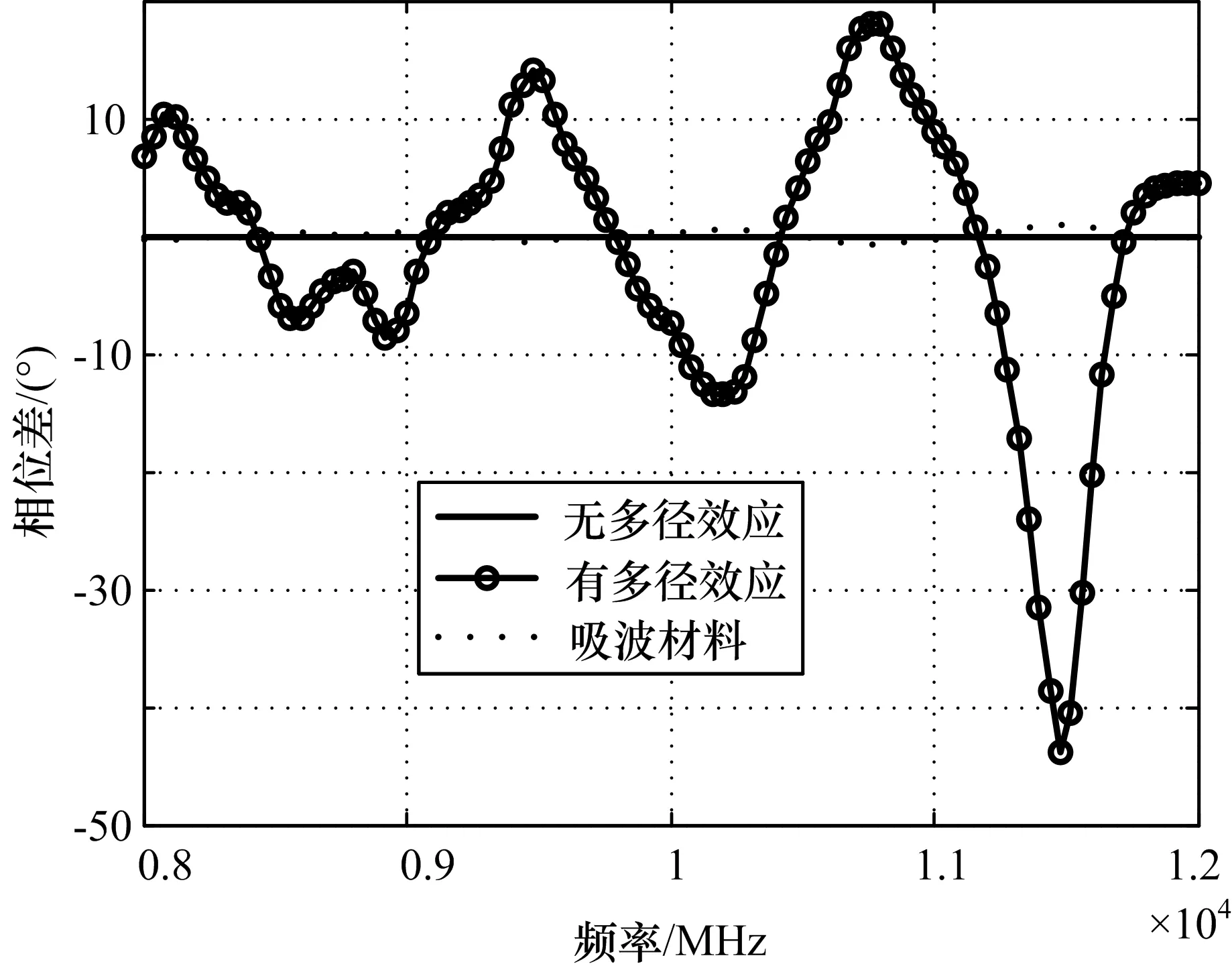
图13 多径效应对AD通道相位差影响

4 结束语

干涉仪测向方法广泛应用于机载无源探测系统，本文对机载天线在地面进行外辐射校准时多径效应的影响进行了分析，通过实测数据和仿真结果对比表明等效分析的合理性。同时对某干涉仪天线阵外辐射校准时多径效应对通道幅度和通道间相位差的影响进行了分析，结果表明多径响应对外辐射校准的相位差影响较大。因此对于测向精度要求高的无源探测系统，在进行外辐射校准时需要尽可能减小多径效应的影响，如可以通过在反射比较强的区域增加铺设吸波材料。■