基于最优化的广域雷场空间多节点坐标修正算法*

赵建新，张宏映，陈 兵，魏玉龙

（北方自动控制技术研究所，太原 030006）

0 引言

智能雷场是在传统雷场基础上的新型信息化地雷武器系统，将传统不动雷提升为具有按照指令布局、通道自动封锁等信息处理能力的活动雷［1］。针对室外活动节点，传统方法采用GPS进行定位，而在野外环境下，普通GPS模块的定位精度在10 m～15 m。在广域雷场空间中，为实现有效区域封锁，活动雷投放密度较高，各活动雷间距离小于3 m。基于成本和定位精度考虑，在每个活动雷中集成了UWB测距模块，其价格较为低廉，测距精度为米级。只在部分活动雷内部集成了GPS模块，包含了GPS模块的活动雷称为锚节点，其余活动雷称为普通节点，锚节点为普通节点提供基准坐标，普通节点利用锚节点坐标通过三边定位法完成定位。在进行活动雷布局时，根据各锚节点的GPS坐标得到的锚节点分布态势与锚节点实际物理分布情况差距过大，导致所有活动雷间的坐标相对误差过大，不能满足精度要求。因此，需要对各节点坐标进行修正，较大限度降低坐标相对误差。

1 基于最优化的广域雷场空间多节点坐标修正方法描述

GPS的误差包含了公共误差、传播延迟误差等，其误差具有随机性［2］。针对广域雷场空间中GPS坐标相对误差较大的问题，采用了GPS与精准测距相结合的方法，利用UWB测距的高精度［3］，提高节点之间的相对坐标精度。

多节点坐标的修正过程分为4个步骤：

1）划分区域并确定点集；

2）寻找凸多边形；

3）顶点坐标修正；

4）其余节点坐标修正。

1.1 划分区域并确定点集

利用锚节点的GPS坐标，对雷场区域中的各锚节点进行划分，得到多个节点点集。该步骤实质为一个聚类过程，借鉴K-均值聚类算法并结合实际情况完成对锚节点的聚类。已知雷场区域大小，雷场区域中存在m个锚节点（其中m＞9，若m≤9，直接寻找凸多边形），根据锚节点的GPS坐标获得锚节点的分布情况，划分过程如下：

1）为保证划分的每个区域中存在6个左右的锚节点，将初始划分区域数量设为n=m/6。

2）将雷场区域平均划分为n个区域，得到各区域中分布的锚节点，选取与各区域锚节点平均位置距离最近的锚节点作为聚类中心；若该区域中无锚节点，则将该区域归入邻近区域；最终得到n个聚类中心。

3）利用GPS坐标计算各锚节点到各聚类中心的距离，若某个锚节点距离第i个聚类中心更近，则将其归入i中心的点集中；若存在聚类中心的点集为空，则淘汰该聚类中心，将其作为锚节点参与划分；最终得到n个点集。

4）分别计算各点集中的平均位置，选取与平均位置距离最近的点作为新的聚类中心。

5）递归执行步骤3）～步骤4），直到聚类中心不再变化；各聚类中心的点集即为得到的点集。

雷场示意图及聚类过程如图1所示，雷场中存在22个锚节点，将雷场分为4个区域；得到4个初始聚类中心，图1中的星形即为各聚类中心；执行步骤3），淘汰聚类中心4，区域4并入区域3；执行算法，最终得到的聚类结果如图1所示，得到3个点集。

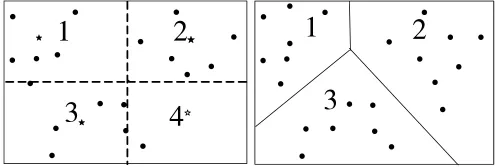
图1 雷场示意图及聚类过程

1.2 寻找凸多边形

分别在每个点集中递归寻找m个锚节点（其中m≥3），各锚节点可以组成一个凸多边形。

以点集M中最靠近中心位置的点作为原点O，建立高斯坐标系，将剩余点分配到各象限中，将集合中M的点按照与原点的距离远近重新排序。

推理得到，已知凸多边形N，其边数为n，判断某一点B能否与其组成凸n+1边形的条件为：

1）B点不在多边形N内；

2）多边形各相邻边反向延伸得到n个区域，B点不在这些区域内。

以四边形为例，如图2所示，若点B不在四边形 N 内，且不在区域 P1、P2、P3、P4内，则 B 可与四边形N组成凸五边形。

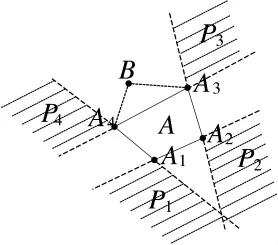
图2 四边形与点B组成凸五边形条件示意图

采用直接法寻找凸多边形，如图3所示，步骤如下：

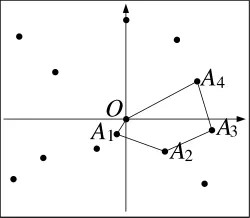
图3 直接法寻找凸多边形

1）以原点O为圆心，将集合M中与原点距离小于0.2 m的节点剔除，遍历寻找M中与原点距离最近的点A1。

2）在集合M中寻找点A2，使得A2与A1、O点可以组成三角形。

3）遍历寻找A3点，A3可与找到的点组成凸多边形，过程中对不满足条件的点进行剔除。

4）递归执行步骤3），直至完成遍历。

1.3 顶点坐标修正

得到凸多边形后，利用节点坐标修正模型对各顶点进行修正，得到修正坐标。

1.4 其余节点坐标修正

分别利用各点集中的凸多边形顶点坐标，通过三边定位方法计算各点集中其余锚节点坐标，再利用测距结合三边定位方法得到各普通节点坐标。

2 节点坐标修正模型

从某一点集中获取凸多边形后，利用UWB测距值结合GPS坐标对顶点坐标进行修正。

2.1 模型建立

假设获取的凸多边形为M，其边数为k，已知M中k个顶点的GPS坐标，利用GPS坐标可以确定M的形状和位置；利用UWB测距可以得到各顶点间两两距离。通过三角形稳定性原理，在得到了多边形M的所有边和对角线的精准长度后，可以确定一个新的多边形N。由于UWB的精度远高于GPS，故多边形N的形状比M更符合各顶点的实际分布形状。当多边形边数为6时的M和N的示意图，如图4所示。

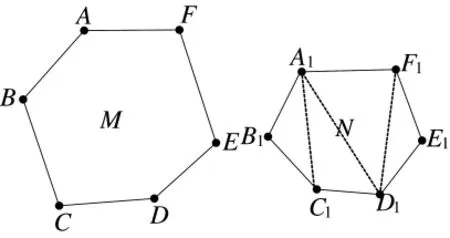
图4 六边形示意图

已知多边形M中各顶点坐标，得到M的中心O，将多边形N的中心与O重合，M不动，以O为圆心旋转多边形N，当N的各顶点距离与M的各顶点的距离和最小时，多边形N的各顶点坐标即为修正后的坐标。当多边形边数为6时的修正示意图如图5所示，图中要求（AA1+BB1+CC1+DD1+EE1+FF1）最小。

算法转化为最优化问题［4］，假设多边形边数为k，则 k 边形 M 中各顶点的坐标为（α1，β1），…，（αk，βk），k 边形 N 中各顶点的坐标为（x1，y1），…，（xk，yk），约束条件如下：

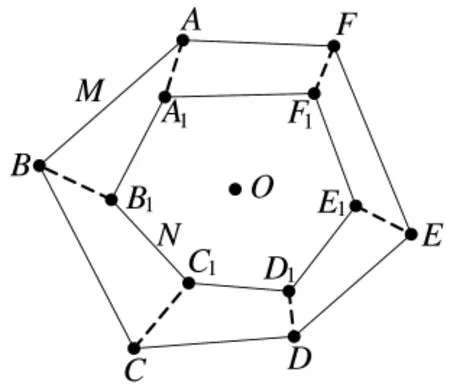
图5 修正示意图

1）k边形N和k边形M的中心O重合；

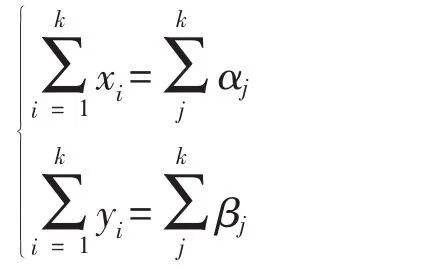
2）k边形N各边距离和对角线距离dij（其中i≠j）已知；

求k边形N各顶点与k边形M各顶点距离和最小，得到目标函数如下：

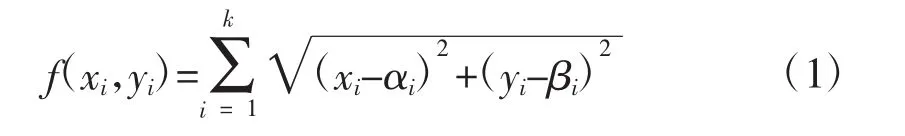
最优化问题通常采用拉格朗日乘子法将带约束条件的最优化问题转化为解方程组问题，当方程组维度超过8时，求得最优解的方法较为复杂且费时［5］，模型通过对多边形进行顺时针旋转，将多维问题优化为一维问题。

2.2 模型优化

以k边形M的中心O为原点建立高斯坐标系，k边形N的中心与O重合，已知M中顶点坐标分别为（α1，β1），…，（αk，βk），N 中各边长度和各对角线长度dij（其中i＝1，…k；j=1，…k；i≠j），推导得出原点O与某一顶点长度为：

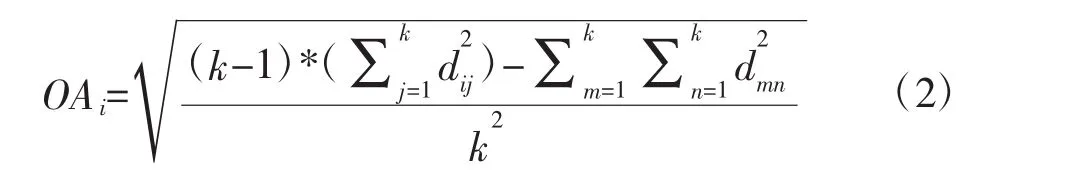
其中，j≠i，m≠n≠i。

以五边形为例，O与A1之间的距离为：

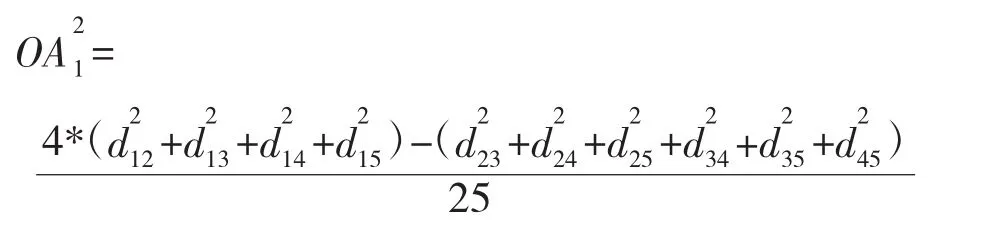
将N中的顶点A1的横坐标设为X1，通过式（2）得到，结合X1得到A1的纵坐标Y1，进而得到k边形N中其余各顶点的初始坐标。

以O为圆心，k边形N以顺时针进行旋转，旋转角度为θ，旋转过程中k边形N各顶点坐标为：

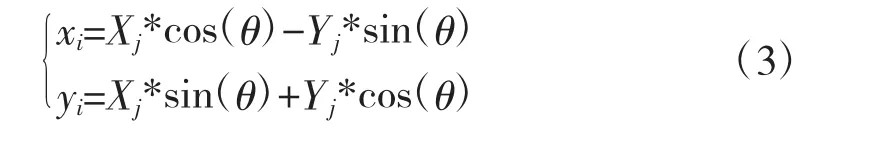
其中，i=1，…k；Xj≠Yj为各项点初始坐标。

旋转模型示意图如图6所示。

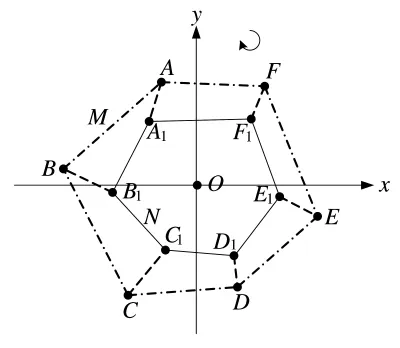
图6 旋转模型示意图

通过旋转使得N的各顶点距离与M的各顶点的距离和最小，结合式（3）得到目标函数为：

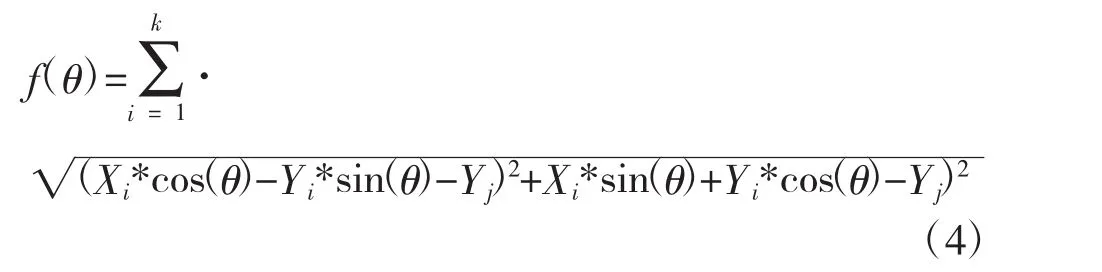
其中，Xj，Yj为各项点初始坐标。

模型最终转化为求单变量θ使f（θ）值最小的问题，通过极值法得到θ值后，将θ带入式（3）中，得到各顶点的修正坐标。

3 算法实验测试

实验选择90*90 m的区域作为雷场区域，选取总共40颗活动雷，其中锚节点15个，其余为普通节点，各活动雷在雷场区域随机分布，节点实际分布示意图如图7所示。其中，用圆圈表示的节点为锚节点，雪花表示的节点为普通节点。

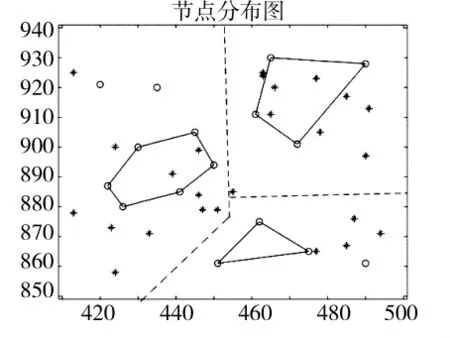
图7 节点分布图

对区域所有节点执行修正算法，将雷场区域划分为图8中虚线分割的3个区域，每个区域中的节点组成一个点集，各点集中分别寻找出六边形、四边形和三角形。

分别对3个多边形执行坐标修正，以六边形为例，各顶点的修正结果如图7所示。图中短划线组成的六边形的6个顶点为锚节点实际分布位置，点虚线组成的六边形的6个顶点为锚节点利用GPS得到的坐标分布位置，实线组成的六边形的6个顶点为经过校准后的坐标分布位置。

图8 校准结果

最终修正过后的所有节点态势分布图与实际分布图对比，如图9所示。

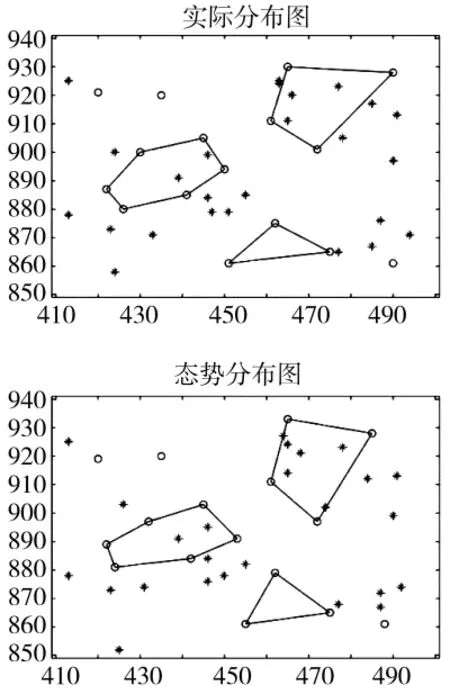
图9 修正后的态势分布与实际分布对比

4 结论

从实验结果来看，利用GPS得到的坐标与锚节点实际分布存在较大偏差，通过节点修正模型以提高锚节点坐标与实际分布的一致性，降低各节点之间坐标的相对误差。在实际应用中，算法还有很多地方需要改善，如稳定性方面需要进一步提高。