基于MATLAB和矩阵位移法的平面杆系结构有限元程序设计
阙仁波
(厦门大学嘉庚学院土木系 福建漳州 363105)
0 引言
在结构力学发展史上,为了解超静定结构,19世纪建立了力法。但用于解之后大量出现的高次超静定刚架,仍显繁琐。在20世纪初,以力法为基础,发展求解高次超静定结构比力法更具优势的位移法[1],但随着基本未知量的增多,位移法的手算法依然让人不堪重负。随着计算机的发展,位移法被以矩阵的方式来表达,即矩阵位移法,以适合编程计算,从而在传统手算法的基础上,发展了程序结构力学,极大地增强了求解高次超静定结构的能力,并将设计者很大程度地从繁琐的计算中解放出来,将更多的精力用于概念设计和定性分析[1-2]。
在适合杆件结构的矩阵位移法的启示下,又发展了适合连续体的矩阵方法——有限元法,故把矩阵位移法称为杆件有限元法[3-6],但相对于连续体有限元法,门槛低,故若由此入门,将其核心思想、计算流程和程序编制掌握,然后,再拾阶而上,在求同中类比而广义化,在变异中对比而延拓,从一维杆件、线性(线性代数之线性、本构关系之线性)到多维连续体、非线性,不断朝横向和纵深发展,不仅难度梯度比直接由弹性力学有限元入门小得多,亦容易建构起合理而有序的知识体系。
此外,杆件有限元在土木工程的专业课中应用较多,比如从总体受力来看,桥梁的特点是长而不宽,它的受力特性与杆系结构相符,一般采用平面杆系有限元法来分析[7]。但对土木专业的本科生而言,有限元大多只是选修课,而在专业软件如桥梁博士和PKPM中,却要用到有限元的概念,故在必修的矩阵位移法教学中体现一点有限元的思想对后续课程学习有较大帮助。
而现在的矩阵位移法教学却存在一些问题。一方面,可能受学时所限或学生没修过编程课,教学只局限于原理的讲解,而线性代数与结构力学的无“机”结合,使得缺乏程序实现而采用手算的矩阵位移法,不仅没显示出其相对于传统位移法和渐进法的优越性,反而让学生更加望而却步,该部分内容的内在规律呼唤理论教学和程序实现的有“机”结合。另一方面,某些观念认为,都那么多现成的软件,没必要再自主开发。可在输入和输出之间,作为内核的有限元对很多程序使用者而言却是“黑盒子”[4],尽管程序设计的智能化造就了软件应用的机械化,但若不加理解,面对复杂问题时出错的可能性会增大。而对于一个从事过开发的人而言,在应用别人开发的软件时,会有一种同理心的优势,站在开发者的角度来审视软件,透视其内核而不觉其内黑,从而能更快更好地掌握软件的应用,并在欣赏中继承,在批判中创新。在“计算机+”和人工智能的时代,这种同理心有助于更好地去理解和适应“机”智的内在原理。此外,对一些不在“通用”之列的个性化问题,亦要靠自主开发程序来解决。故编程训练仍有其存在的必要性。且矩阵位移法所蕴含的从一般到特殊的演绎(如从刚架到连续梁、桁架和组合结构)、化整为零的单元分析、集零为整的整体综合思想,更具有方法论上的意义。通过编程,可提高一个人对复杂系统内在逻辑认识的清晰度,将复杂系统分解为简单子系统逐个加以处理,然后再加以集成,可将“知识单元”富有逻辑地集成为“知识整体”,从“构件”到“结构”,建构起牢固而“几何不变的知识体系”。
基于矩阵位移法的程序开发,可采用不同的语言,如Fortran[2,8]、C++[5]和VB[9]等。而采用以擅长矩阵计算著称的MATLAB(即矩阵实验室)来处理“矩阵位移法”之“矩阵”,将会是一种非常具有优势的选择,且该语言简单易学,应用更广泛,故目前采用MATLAB编写的程序开始增多[4,6,10-13],但这些资料中,要么从弹性力学和一般有限元开始讲解[4,6,10],对于本科生来说,难度相对较大;要么将连续梁、桁架和刚架分门别类地讲[11,12],篇幅较大。如何与结构力学教材直接配套,在一边理论教学的同时,一边快速切入程序实现,而无需过多参考资料,以较小的跨度在传统手算和程序计算之间架起一座沟通的桥梁,对大多数受学时所限的本科教学来说,是非常必要的。此外,以较短的时间让学生一窥从理论到程序实现的全过程,可更好地激起他们的兴趣,然后再去拓展,教学效果会更好。而通过阅读程序、修改程序到自主编程逐步进阶,不失为一种入门的方法。
鉴于上述目的,本文将基于目前高校广泛采用的结构力学教材—文献[14](尽管它配套有求解器,为文献[2]的程序实现,但文献[2]是以Fortran语言编写),采用MATLAB语言编写一个程序,以供教学参考。
1 程序概况
(1)流程图和源代码请见附录。
(2)该程序充分发挥了MATLAB擅长矩阵计算的优势,代码十分简洁,除注释行外,才115行。
(3)该程序基于文献[14]编写,故对采用该教材的师生,参照非常方便。符号系统同文献[14],故限于篇幅,本文不再赘述。
(4)可自行控制输出,比如输出局部坐标系中的单元刚度矩阵、坐标转换矩阵、整体坐标系中的单元刚度矩阵等阶段性结果,以配合阶段性演示或检验。
(5)为便于没学过有限元英文专业词汇的学生记忆,程序中的变量名大多采用汉化的表述模式,如JJHZ-结间荷载,JDHZ-结点荷载。
2 编写说明
(1)该程序按分析刚架的一般模式编写。
(2)对于边界条件,均采用先处理法,即令结点位移为零的总码为零,如图3所示。
(3)将连续梁和桁架看作特殊的刚架,具体处理方式如下:
①对于连续梁(忽略轴向变形),每个单元亦按6个杆端位移输入,令4个线位移总码为零即可;
②对于桁架,每个单元亦按6个杆端位移输入,但同一铰结点处各杆的结点线位移相同,故采用重码;但结点角位移不同,故采用异码。如图7中单元①、②和⑤交点处的编码。
③上述处理模式对于单纯的连续梁和单纯的桁架结构,可能比按单纯计算连续梁和桁架的程序显得麻烦。但本文中,一方面更注重程序的通用性,希望以一般而非特殊的思维来统一看待不同类型的结构;另一方面,本文的方法在处理诸如例四所示的组合结构时,就显示出其优越性。
(4)组合结点处,编码时要注意线位移的重码和转角的异码问题,如例四中A点和B点处。
3 数据准备和输入
3.1 准备工作
(1)划分单元

②对结点位移编码,以确定单元定位向量。
(3)确定单元的结间荷载。
(4)确定单元的结点荷载。
3.2 输入工作
(1)BM——编码矩阵:每一行第1列元素代表单元号,第2~7列元素代表该单元定位向量(以行向量形式输入)的6个元素。
(2)CLJ——材料参数和夹角矩阵:每一行第1列元素代表单元号,第2~6列元素分别代表该单元的弹性模量E、截面面积A、截面惯性矩I、长度l和夹角α。
(3)JJHZ——结间荷载矩阵:每一行第1列元素代表单元号,第2~5列元素分别代表该单元的荷载类型号、荷载大小(q、Fp、M)、a和b,如表1所示。
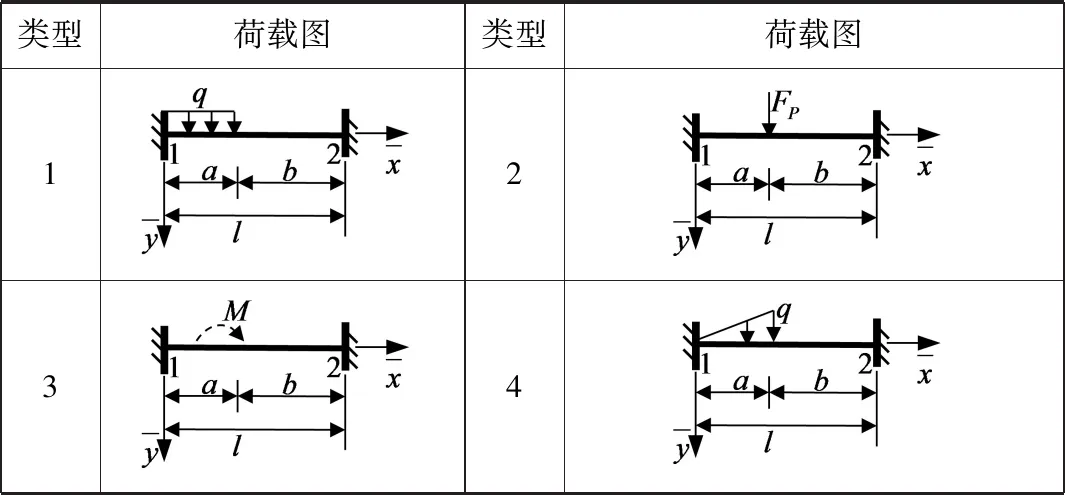
表1 荷载类型
该程序只考虑了表1所示的4种情况,更多可参阅文献[14]表11-2,读者可在求单元固端约束力的子程序function[GDL]=g(LX,F,a,b)中增加case即可扩展荷载类型、考虑支座移动或温变的影响。
输入JJHZ时要注意:
①有荷载的单元才需输入;
②当同一单元有多种荷载,每一种均需输入,如例一的单元1;
③若所有单元均无结间荷载(如桁架的情形),则JJHZ为空矩阵,如例三。
(4)JDHZ—结点荷载矩阵:每一行第1列元素代表结点荷载所对应的结点位移编码,第2列元素代表结点荷载大小。如例三中JDHZ=[1 10;2 -10]。若所有结点均没荷载作用,则JDHZ为空矩阵,如例一、例四和例五。
4 结果输出和控制
(1)一般控制输出的结果为:
①结点位移向量Δ即程序中的Delta;
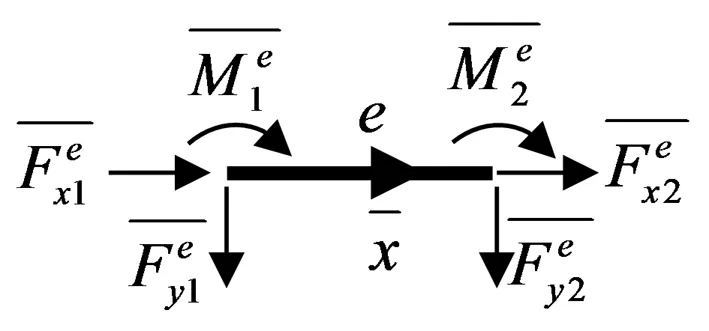
图1 局部坐标系中的单元杆端力
(2)用户可自行控制参数的输出,只需在function[ ]=f(BM,CLJ,JJHZ,JDHZ) 左侧方括号中填入或修改需要输出的参数即可。如例二,[DeltaT,GDNLT]=f(BM,CLJ,JJHZ,JDHZ)。习惯于行向量输出还是列向量输出,只需通过在程序中转置即可实现。亦可输出阶段性结果,以配合阶段性演示或检验的需要。
5 算例
注:荷载作用下,超静定结构的内力分布只与各杆的相对刚度有关,与绝对刚度无关,而位移与绝对刚度有关。故在以下算例中,当各杆的E、A、I值以相对大小输入时,算出的内力属于真实值,而位移真实值则需输入实际的绝对值进行计算。
为体现程序的通用性,算例的选择上着重体现结构类型、支座类型、截面变化情况和荷载类型的多样化。
5.1 例一 用程序计算图2所示刚架的杆端内力

图2 刚架算例
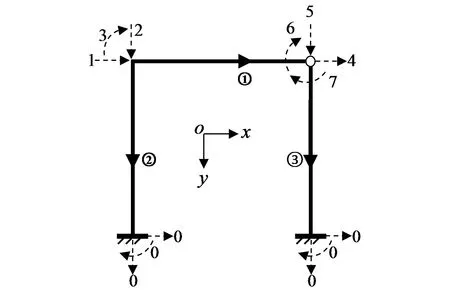
图3 坐标建立、单元划分和结点位移编码
(1)输入
>>BM=[1 1 2 3 4 5 6;2 1 2 3 0 0 0;3 4 5 7 0 0 0];
>>CLJ=[1 1 0.6 1/6 5 0;2 0.9 0.5 1/12 5pi/2;3 0.9 0.5 1/12 5pi/2];
>>JJHZ=[1 1 4.8 5 0;1 2 6 4 1;3 2 -8 2 3];
>>JDHZ=[];
(2)执行
>>[GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
(3)输出
Elapsed time is 0.133784 seconds.
GDNLT=

5.2 例二 用程序计算图4所示连续梁的杆端内力和杆端位移
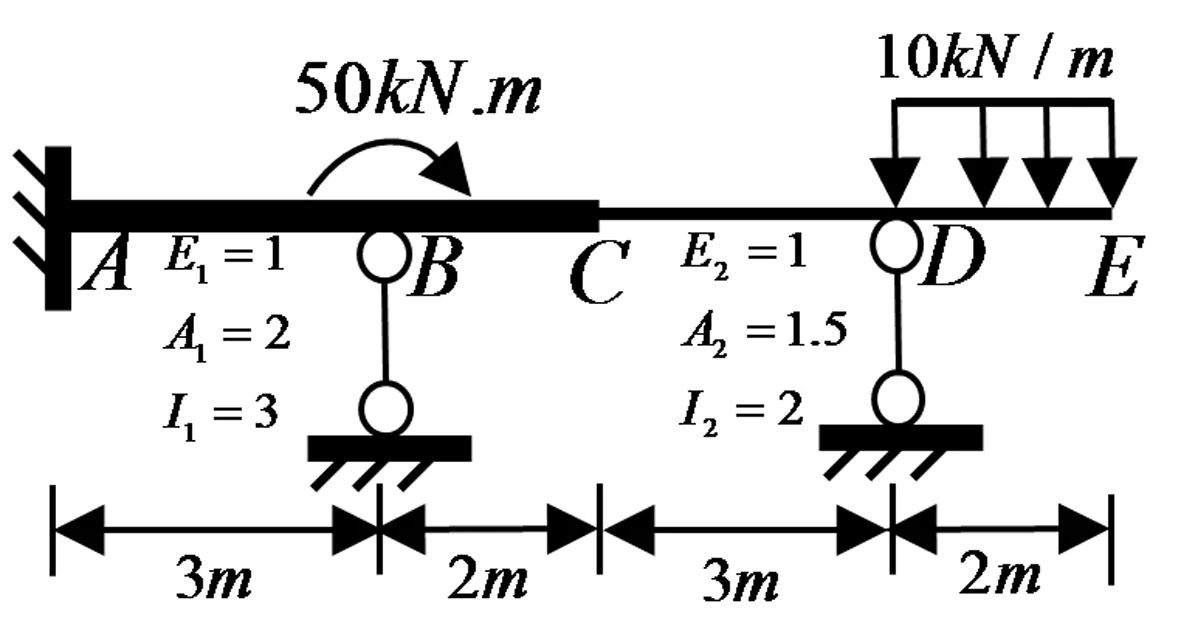
图4 连续梁算例
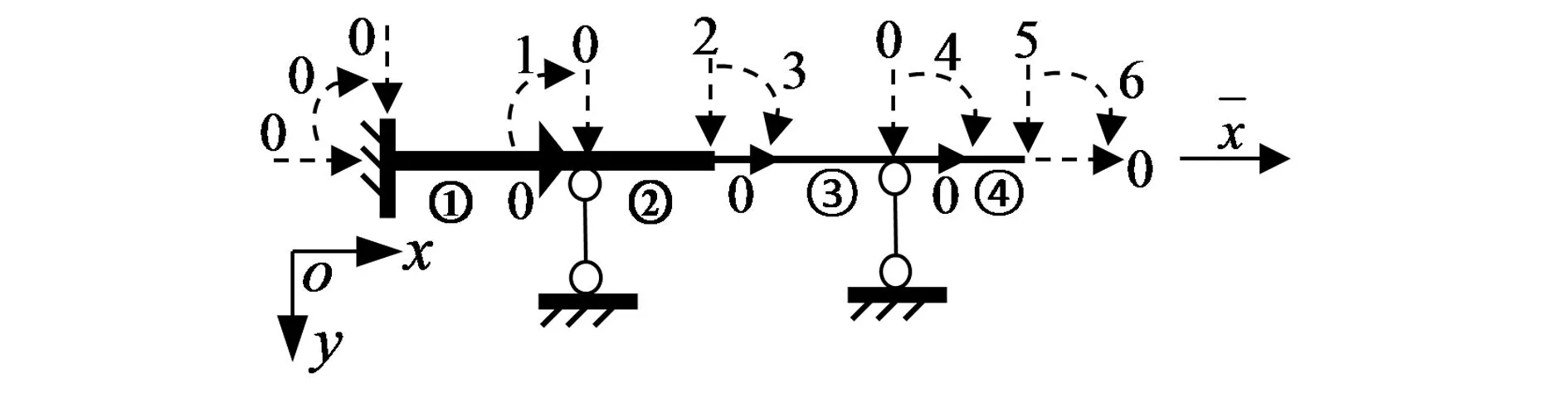
图5 坐标建立、单元划分和结点位移编码
(1)输入
>>BM=[1 0 0 0 0 0 1;2 0 0 1 0 2 3;3 0 2 3 0 0 4;4 0 0 4 0 5 6];
>>CLJ=[1 1 2 3 3 0;2 1 2 3 2 0;3 1 1.5 2 3 0;4 1 1.5 2 2 0];
>>JJHZ=[4 1 10 2 0];
>>JDHZ=[1 50];
(2)执行
[DeltaT,GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
(3)输出
Elapsed time is 0.024951 seconds.
DeltaT=
6.76512.0539-2.80277.874425.748814.5411
GDNLT=

5.3 例三 用程序计算图6所示桁架的杆端内力

图6 桁架算例

图7 坐标建立、单元划分和结点位移编码
(1)输入
>>BM=[1 1 2 5 0 0 6;2 1 2 7 3 4 8;3 3 4 9 0 0 10;4 0 0 11 0 0 12;5 1 2 13 0 0 14 ;6 3 4 15 0 0 16 ];
>>CLJ=[1 1 1 1 1pi/2;2 1 1 1 1 0;3 1 1 1 1pi/2;4 1 1 1 1 0;5 1 1 1 2^0.5pi/4;6 1 1 1 2^0.5 3*pi/4];
>>JJHZ=[];
>>JDHZ=[1 10;2 -10];
(2)执行
>>[GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
(3)输出
Elapsed time is 0.026574 seconds.
GDNLT=

5.4 例四 用程序计算图8所示组合结构的杆端内力

图8 组合结构算例

图9 坐标建立、单元划分和结点位移编码
(1)输入
>>BM=[1 0 0 0 1 2 3;2 1 2 3 4 5 6;3 4 5 6 0 0 0;4 0 0 7 1 2 8;5 4 5 9 0 0 10];
>>CLJ=[1 1 2 1 20 0;2 1 2 1 20 0;3 1 2 1 20 0;4 1 1/20 1 25 atan(3/4);5 1 1/20 1 25 -atan(3/4)];
>>JJHZ=[2 1 10 20 0];
>>JDHZ=[];
(2)执行
>>[GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
(3)输出
Elapsed time is 0.025520 seconds.
GDNLT=
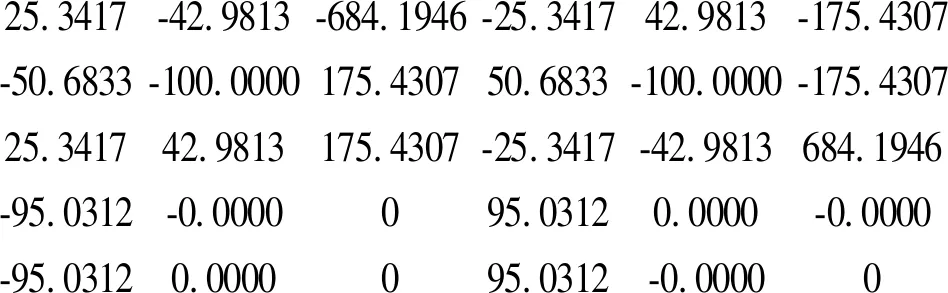
5.5 例五 用程序计算图10所示刚架的杆端内力

图10 带滑动支座的刚架算例

图11 坐标建立、单元划分和结点位移编码
(1)输入
>>BM=[1 1 0 2 3 4 5;2 3 4 5 0 6 0;3 3 4 5 0 0 0];
>>CLJ=[1 1 1 1 4 0;2 1 1 2 2 0;3 1 1 1 4 pi/2];
>>JJHZ=[1 2 10 2 2];
>>JDHZ=[ ];
(2)执行
>>[GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
(3)输出
Elapsed time is 0.003276 seconds.
GDNLT =

若忽略轴向变形,则可在CLJ中令A为一个大数,比如A=106,则CLJ=[1 1 10^6 1 4 0;2 1 10^6 2 2 0;3 1 10^6 1 4 pi/2],重新执行可得:
GDNLT=

6 结语
(1)基于MATLAB语言和矩阵位移法思想,进行了平面杆系结构有限元程序设计。该程序注重通用性,对刚架、连续梁、桁架及组合结构,都采用统一的分析模式,这对分析组合结构尤其具有优势。
(2)该程序充分发挥了MATLAB——矩阵实验室擅长矩阵计算的优势,代码简洁,数据准备简单、计算流程清晰、结果输出可选控,可作为矩阵位移法原理学习之外的一种实践补充,与教材紧密配套,切入方便快捷,以较低的门槛,引领学生初窥有限元。
(3)该程序旨在抛砖引玉,读者可在此基础上进一步修改拓展,以处理更多实际情况,比如增加荷载类型、考虑支座位移和温变的影响、考虑斜支座和弹性支座、考虑剪切变形和带刚域杆[15]、基于MATLAB GUI开发可视化图形用户界面和内力图自动绘制功能等,进一步增加其通用性和智能化程度。
7 附录:流程图和源代码

图12 计算流程图
function [GDNLT]=f(BM,CLJ,JJHZ,JDHZ)
tic %计时开始
DYSH=max(BM(:,1)); %计算单元数
ZDM=max(max(BM(:,2:7))); %计算最大总码
K=zeros(ZDM,ZDM); %将整体刚度矩阵赋初值零
FeP=zeros(6,DYSH); %将由局部坐标系中的固端约束力向量按列连接而成的矩阵赋初值零
P=zeros(ZDM,1); %将整体结构的等效结点荷载向量赋初值零
GDWY=zeros(6,DYSH);%将由局部坐标系中的单元杆端位移向量按列连接而成的矩阵赋初值零
GDNL=zeros(6,DYSH);%将由局部坐标系中的单元杆端内力向量按列连接而成的矩阵赋初值零
for N=1:DYSH
%计算局部坐标系中的单元刚度矩阵
kej=zeros(6,6);
EAL=CLJ(N,2)*CLJ(N,3)/CLJ(N,5);
kej([1 4 19 22])=[EAL -EAL -EAL EAL];
EIL3=12*CLJ(N,2)*CLJ(N,4)/CLJ(N,5)^3;
kej([8 11 26 29])=[EIL3 -EIL3 -EIL3 EIL3];
EIL2=6*CLJ(N,2)*CLJ(N,4)/CLJ(N,5)^2;
kej([9 12 14 32])=EIL2;
kej([17 27 30 35])=-EIL2;
kej([15 36])=4*CLJ(N,2)*CLJ(N,4)/CLJ(N,5);
kej([18 33])=2*CLJ(N,2)*CLJ(N,4)/CLJ(N,5);%将所有局部坐标系中的单元刚度矩阵按行连接生成一个大矩阵,以供后面求局部坐标系中的单元杆端内力向量时调用
kejall((N*6-5):N*6,:)=kej;
%单元坐标转换矩阵
T=zeros(6,6);
T([1 8 22 29])=cos(CLJ(N,6));
T([7 28])=sin(CLJ(N,6));
T([2 23])=-sin(CLJ(N,6));
T([15 36])=1;
Tall((N*6-5):N*6,:)=T; %将所有局部坐标系中的单元坐标转换矩阵按行连接生成一个大矩阵,以供后面求局部坐标系中的单元杆端位移向量时调用
kezh=T'*kej*T; %整体坐标系中的单元刚度矩阵
%定位
FL=0;
for M=2:7
if BM(N,M)~=0
FL=FL+1; %统计单元中非零总码的个数
BMFL(FL,:)=[M-1,BM(N,M)]; %找出局部码(M-1)与总码(B(N,M))对应关系
end
end
%累加
for I=1:FL
for J=1:FL
K(BMFL(I,2),BMFL(J,2))=K(BMFL(I,2),BMFL(J,2))...
+kezh(BMFL(I,1),BMFL(J,1));
end
end
%求局部坐标系中的单元固端约束力
SZJJ=size(JJHZ);
if SZJJ(1,1)~=0 %若结间作用荷载
for S=1:SZJJ(1,1)
if JJHZ(S,1)==N
[GDL]=g(JJHZ(S,2),JJHZ(S,3),JJHZ(S,4),JJHZ(S,5));
%调子函数
FeP(:,N)=FeP(:,N)+GDL; %单元固端约束力(局部坐标系中)
end
end
end
Pe(:,N)=-T'*FeP(:,N); %整体坐标系中的单元等效结点荷载向量
%将Pe在P中定位累加
for S=2:7
if BM(N,S)~=0
P(BM(N,S),1)= P(BM(N,S),1)+Pe(S-1,N); %整体结构的等效结点荷载向量
end
end
end
%将结点荷载在P中定位累加
SZJD=size(JDHZ);
if SZJD(1,1)~=0; %若作用结点荷载
for Z=1:SZJD(1,1)
P(JDHZ(Z,1),1)= P(JDHZ(Z,1),1)+JDHZ(Z,2);
end
end
Delta=KP; %(编码非零)结点位移向量,按编码从小到大的顺序排列
DeltaT=Delta'; %转置成行向量表示
for II=1:DYSH
for JJ=2:7
if BM(II,JJ)~=0
GDWY(JJ-1,II)=GDWY(JJ-1,II)+Delta(BM(II,JJ),1);
%由结点位移向量求整体坐标系中的单元杆端位移
end
end
DYWY=Tall((II*6-5):II*6,:)*GDWY(:,II); %局部坐标系中的单元杆端位移
GDNL(:,II)=GDNL(:,II)+...
kejall((II*6-5):II*6,:)*DYWY+ FeP(:,II); %局部坐标系中的单元杆端内力
end
GDNLT=GDNL'; %转置,以便输出时以每单元一行而非每单元一列,节省文中显示空间
%求解局部坐标系中单元杆端约束力的子函数
function [GDL]=g(LX,F,a,b)
L=a+b;
switch LX %判断荷载类型
case 1
FxP1=0;
FxP2=0;
FyP1=-F*a*(1-a^2/L^2+a^3/(2*L^3));
FyP2=-F*a^3/L^2*(1-a/(2*L));
MP1=-F*a^2/12*(6-8*a/L+3*a^2/L^2);
MP2=F*a^3/(12*L)*(4-3*a/L);
GDL=[FxP1 FyP1 MP1 FxP2 FyP2 MP2]';
case 2
FxP1=0;
FxP2=0;
FyP1=-F*b^2/L^2*(1+2*a/L);
FyP2=-F*a^2/L^2*(1+2*b/L);
MP1=-F*a*b^2/L^2;
MP2=F*a^2*b/L^2;
GDL=[FxP1 FyP1 MP1 FxP2 FyP2 MP2]';
case 3
FxP1=0;
FxP2=0;
FyP1=6*F*a*b/L^3;
FyP2=-6*F*a*b/L^3;
MP1=F*b/L*(2-3*b/L);
MP2=F*a/L*(2-3*a/L);
GDL=[FxP1 FyP1 MP1 FxP2 FyP2 MP2]';
Otherwise
FxP1=0;
FxP2=0;
FyP1=-F*a/4*(2-3*a^2/L^2+1.6*a^3/L^3);
FyP2=-F/4*a^3/L^2*(3-1.6*a/L);
MP1=-F*a^2/6*(2-3*a/L+1.2*a^2/L^2);
MP2=F*a^3/(4*L)*(1-0.8*a/L);
GDL=[FxP1 FyP1 MP1 FxP2 FyP2 MP2]';
end
end
toc %计时结束
end

