基于因子分解机和隐马尔可夫的推荐算法

王晓耘，李 贤，袁 媛

(1.杭州电子科技大学 管理学院，浙江 杭州 310018；2.杭州电子科技大学 计算机学院，浙江 杭州 310018)

0 引 言

近年来，随着互联网技术的飞速发展，数据呈现出了爆炸式的增长。如何快速又有效地从海量数据中寻找用户所需要的信息成为了一个迫切的问题。为了应对海量的数据信息，搜索系统和推荐系统应运而生。对于那些有着明确目的的用户，信息搜索系统是一种非常有效的方法，但通常用户并不是非常清楚自己所需要什么，在这种情况下使用推荐系统便是一个较好的应对策略，现如今推荐系统的应用已经遍布网络的各个领域。协同过滤是一种常见且有效的推荐方法，协同过滤是通过寻找与当前用户最相似的用户，根据相似用户的历史购买记录来进行推荐的。此外还有基于内容的推荐方法和其他一些传统的推荐方法，这类传统的推荐方法起初往往在推荐过程中并不会引入上下文信息，这导致在推荐精度存在一些不足。在这种情况下，研究者们开始在推荐系统中引入上下文信息，通过结合上下文信息来对用户进行个性化推荐。这便出现了将传统的“用户-产品”二维的评分模型User×Item→Rating扩充为含有上下文信息的模型User×Context×Item→Rating。

文中主要基于上下文信息来对用户进行个性化推荐，提出了一种结合因子分解机[1]和隐马尔可夫模型的方法来进行个性化推荐，通过因子分解机进行初始预测，之后利用隐马尔可夫模型对用户的兴趣爱好进行预测，从而为用户进行个性化推荐。通过引入上下文信息来构建包含用户和产品的上下文信息矩阵，但该矩阵通常是稀疏矩阵，而因子分解机能够较好地对稀疏矩阵进行学习，能够较好地解决实际情况中一些数据稀疏的问题，而拥有隐藏状态的隐马尔可夫模型则能够模拟以用户兴趣为隐藏状态的用户评分模型。在MovieLens数据集上的实验结果表明，该方法能够有效提高个性化推荐的准确度。

1 相关工作

1.1 推荐算法

目前推荐系统[2-4]可以分为两类：上下文感知推荐系统和非上下文感知推荐系统。它们之间的主要区别可以表述如下。对于一个用户集合U={u1,u2,…,um}和一个产品集合I={i1,i2,…,im}，传统的推荐技术即非上下文感知推荐系统，是基于用户对产品的评分矩阵M∈Rm×n来进行的，通过拟合矩阵特征模型来预测那些空白的数据，这类被称为非上下文感知的推荐。这种推荐模型能够适应很多的案例，但那些上下文信息，例如：时间、地点、用户情绪等[5]并未参与其中。这些信息能为推荐提供更多的维度。可以为上下文信息[6]定义一系列上下文的维度{C3,C4,…,Ck}，每个上下文维度Ci是由一系列在某一情境下所捕获的属性集所组成的。事实上用户和产品也可以由上下文维度C1,C2来表示。

使用用户对产品的评分来进行个性化推荐，在部分情况下有着不错的效果，但在许多应用场景下并不能进行精确的推荐。上下文感知推荐系统是通过利用用户以及产品的额外信息来构建适应面更加广泛的推荐系统，以达到提高个性化推荐准确度的目的，具有重要的研究意义和应用价值。

通常用户的选择是受当前上下文信息影响的，包括时间、地点、人物、环境等等。Karatzoglou等[7]提出了一种将用户，产品，上下文信息作为N维张量的多层推荐模型。对特征因子采用了高阶奇异值分解。然而，这种模型只能应用在一些特定的上下文信息之中，而且计算复杂度较高。Rendle等[8]通过使用因子分解机(FM)来进行上下文感知推荐。因子分解机中可以将大量的上下文信息转换到特征矩阵中。与多层推荐模型相比，因子分解机具有较短的计算时间，并且在预测结果和预测的质量上都要优于多层推荐模型。Hong等[9]提出了一种co-FM方法来对用户的兴趣进行建模，并进行个性化推荐。Cheng等[10]提出了一种具有损失函数的因子分解机模型，将一种特征选择算法和因子分级机进行合并。Wang等[11]提出了一种随机分割的因子分解机模型来进行上下文感知推荐。在训练随机分割的因子分解机模型之前随机选择树需要手动进行，另外还具有非常高的计算复杂度。Yin[12-15]等采用主题模型进行兴趣点推荐，利用一个包含隐藏变量的中间层以及用户和产品空间的链接，但该模型面对大量信息时效果不佳。

1.2 隐马尔可夫模型

隐马尔可夫模型的主要特点是具有隐藏的状态序列，以及在观测序列的一般随机过程。目前，基于隐马尔可夫模型的改进包括对隐马尔可夫模型的改进和将隐马尔可夫模型与其他模型的结合。文献[16-17]将一阶隐马尔可夫模型改为二阶隐马尔可夫模型，这在实际应用中能更加符合对象特征，但算法的计算复杂度将会是一个重要的问题。Krishnalal[18]提出一种将隐马尔可夫模型和支持向量机相结合的方法，先使用隐马尔可夫模型进行预分类，再使用支持向量机进行二元分类。为解决小波系数之间的依赖问题，Crouse等[19]提出一种小波域马尔可夫模型，该模型在分类、预测等方面也有不错的表现。

2 方 法

2.1 因子分解机

因子分解机是一种基于矩阵分解的机器学习方法，对于稀疏数据有较好的学习效果。因子分解机[20]的2维模型可表示为：

(1)

在该模型中，模型参数Θ={w0,w1,…,wn,v1,1,…,vn,k}为w0∈R,W∈Rn,V∈Rn×k。并且

(2)

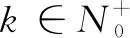
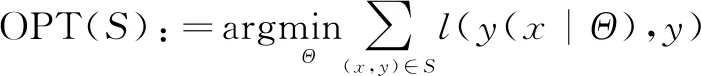
(3)

对于不同的目的，损失函数的选择也可以有所不同，通常采用的是：

lLS(y1,y2):=(y1-y2)2

(4)

或者对于二分类问题(y∈{-1,1})，有：

lC(y1,y2):=-lnσ(y1,y2)

(5)

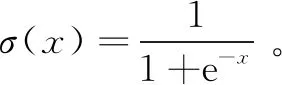
由于FM模型通常含有大量的模型参数Θ，因此容易出现过拟合。可以通过引入正则化进行处理。

(6)

其中，λθ∈R+是模型参数θ的正则化系数。

对于上述优化问题可以采用SGD算法来求解，SGD算法具有较低的计算复杂度和存储复杂度，以及易实现等特点，常用来优化因子分解机模型。参数的更新如下：

(7)

(8)

(9)

(10)

其中，η∈R+是学习速率，也可理解为梯度下降的下降速度。

2.2 隐马尔可夫

一个离散的马尔可夫链是一系列具有马尔可夫性质的随机变量X1,X2,X3…。也就是说下一状态的可能取值只依赖于当前状态，而与历史状态无关。

P(Xn+1=x|X1=x1,X2=x2,…,Xn=xn)=P(Xn+1=x|Xn=xn)

一个马尔可夫模型可以表示为(S,P,Q)，其中S为xi的所有可能取值所构成的可数集，称为该马尔可夫链的状态空间；P=[Pij]n×n是状态转移矩阵，Pij则表示在某一时刻处于状态i而下一时刻处于状态j的概率，其中n表示所有的状态个数；Q={q1,q2,…,qn}是初始的各个状态的概率分布。

隐马尔可夫模型也是一种马尔可夫链，不同的是它的状态转移过程是不可观察的，定义如下：X={s1,s2,…,sn}表示一组状态集合，其中n为状态数；O={v1,v2,…,vm}为一组可观察符号集合，m为观察值的数目；状态转移概率为A={aij}，B={bI(k)}为状态i的观察概率分布，表示状态i为对应观察值的概率；π={πi}表示初始化状态分布。至此，一个隐马尔可夫模型可以定义为：

λ=(X,O,π,A,B)

2.3 推荐方法

在推荐系统中，数据稀疏是一个常见的问题，由于因子分解机能够在稀疏数据中有较好的学习效果。因此，可以使用因子分解机来进行处理。首先构建含有上下文信息的矩阵，如图1所示。

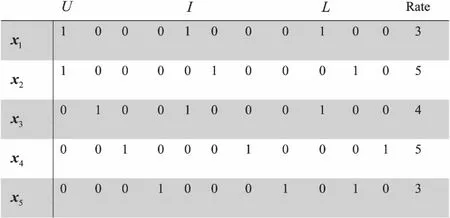
图1 含有上下文信息的矩阵

图1表示用户U={u1,u2,…,um}对于产品I={i1,i2,…,in}在条件L={l1,l2,…,lk}的情况下进行的评分，其中L便是由上下文信息所组成的，在L中可以添加想要加入的上下文信息，当与该信息所描述的情况符合时由1表示，否则为0。例如，第一行的x1向量表示用户u1在l1的条件下对于产品i1的评分为3。在构建完含有上下文信息的矩阵后便可使用因子分解机来进行学习。

用户的兴趣是对用户进行个性化推荐的一个关键点，如果根据用户的兴趣来进行推荐便可大大提高推荐的准确度。用户的兴趣通常来说是无法直接观察到的，但是可以通过用户的历史记录来对用户的兴趣进行猜测。

通过引入隐马尔可夫模型来进行预测操作，以用户的兴趣作为隐马尔可夫模型中的隐藏状态，可以事先手动设置隐含状态集合X，接着根据用户对产品的评分，对每一个用户按照时间的顺序来构建一组可观察符号集合O，之后便可以通过这组可观察的状态序列来对隐马尔可夫模型进行学习。具体的方法可以使用前向后向算法进行，这里就不再进行介绍了。

文中采用的推荐方法的整体流程如图2所示。

首先对数据集进行随机划分，按一定比例分为测试集和训练集。接着对训练数据集构建上下文信息矩阵，再对上下文信息矩阵引入因子分解机来进行求解，便可求得用户评分的初始预测值，之后将初始预测值加入到上述可观察符号集O中，结合用户的历史评分对隐马尔可夫模型进行学习，最后再根据得到的隐马尔可夫模型求解用户对产品的最终预测值。得到最终预测值后便可根据最终预测评分的最高n位来进行推荐。

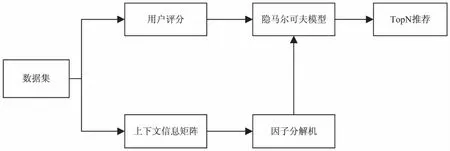
图2 算法流程

3 实 验

3.1 数据集

为验证文中方法的有效性，使用MovieLens-1M和MovieLens-10M数据集，其中MovieLens-1M数据集包含由6 040名用户对于3 900部电影进行的约一百万的评分，而Movielens-10M数据集包含71 567名用户对10 681部电影进行的约一千万的评分。其中评分为1到5星，对于用户记录了用户性别、年龄、职业和邮编，其中对于年龄的划分分为：小于18，18-24，25-34，34-44，45-49，50-55以及大于55。在职业上则进行了20种划分，包括作家、律师、无业游民、大学生等。而对于电影分成18种类型。

用户对电影的评分构成可观察的集合，再根据电影的类型作为用户兴趣集合。而对于上下文矩阵对用户考虑性别、职业和年龄属性。而对于电影则考虑电影类型。此外对用户的评分按照评分时间的顺序构建每个用户的评分序列。在数据上按照80%和20%进行划分，其中20%的测试集合为随机选取，剩余的80%则是训练集。

3.2 评估指标

推荐方法的评价指标有很多，但目前使用较多也是最直接的一类指标是准确度，比较典型的有平均绝对误差(mean absolute error，MAE)。

(11)

另外，均方根误差(root mean squared error，RMSE)也是一个使用较为频繁的指标。

(12)

3.3 实验结果

在对提出的方法(FM-HMM)进行实验时，选择了SVD++[20]和因子分解机(FM)两种方法分别对MovieLens-1M和MovieLens-10M两个数据集进行对比实验，并选择了平均绝对误差和均方根误差作为评估标准。另外SVD++是一种典型的非上下文感知推荐算法，而FM和FM-HMM则是基于上下文信息来进行推荐的。在构建含有上下文信息的矩阵时，对于用户选取了性别、年龄和职业作为上下文信息，在年龄和职业的划分上，采用了数据集所使用的划分方法分别将年龄划分为7段，而对职业则分为21种。对于电影，使用了电影类型来作为上下文信息，将电影分为了18种类型。而在对用户建立按照时间顺序的用户评分序列时，对于使用因子分解机初步预测得到的数据集，选择将这些预测值作为最新的评分来进行排列。

对于两种数据集得到的实验结果如表1和表2所示。分别查看可以明显地发现，上下文感知推荐在误差上明显要低于非上下文感知推荐方法。再对比FM模型和FM-HMM模型可以发现FM-HMM模型表现要略优于FM模型。再对比表1和表2的结果可以发现，当数据量增加时，三种方法在误差上都有相应的减少并且FM-HMM方法减少的量要略微大于FM方法。以上结果表明，引入上下文信息以及隐藏信息来进行推荐是可行的。

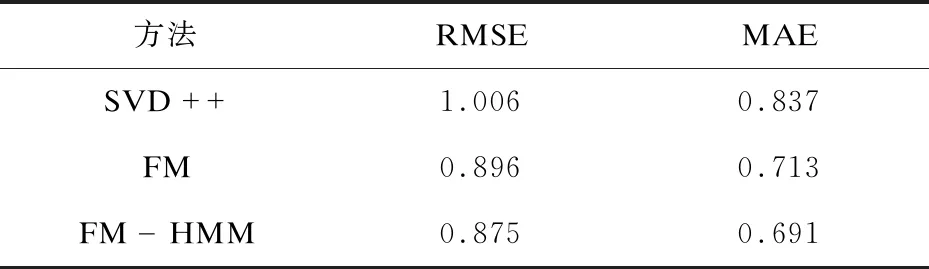
表1 MovieLens-1M数据结果

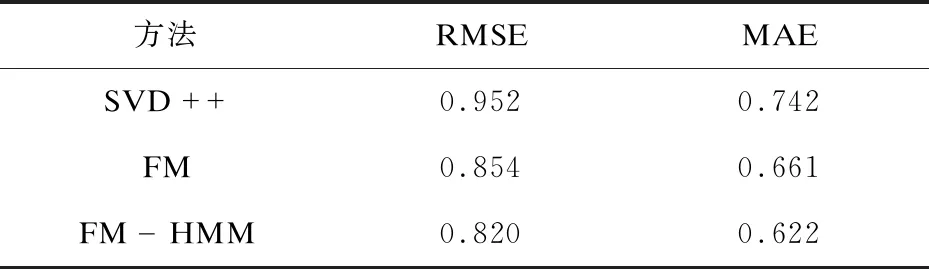
表2 MovieLens-10M数据结果

4 结束语

文中提出了一种应对上下文感知的推荐算法，通过结合因子分解机和隐马尔可夫模型来实现个性化推荐。该算法使用因子分解机进行初始预测，再将用户的兴趣偏好作为隐藏属性来构建隐马尔可夫模型进行预测。通过与其他机器学习方法的对比来验证该方法的有效性，并采用MovieLens数据集进行实验分析。实验结果表明，引入因子分解机和隐马尔可夫模型能够有效地提升推荐结果的准确性。但是文中研究也存在一些不足之处，在对用户的兴趣偏好方面比较依赖具体的应用领域，而且兴趣的选择上也比较单一，今后将会尝试在兴趣的选择上进行更多元化的实现。此外，也会思考如何在大数据平台下进行实现。