置换流水车间调度问题的水波化学反应算法
姜强强,张其亮
(1.浙江大学 软件学院,浙江 宁波 315048;2.江苏科技大学 电气与信息工程学院,江苏 张家港 215600)
0 引 言
置换流水车间调度问题(permutation flow-shop scheduling problem,PFSP)是一类典型的组合优化问题,并已证明是NP难题[1]。PFSP有大批量生产加工的应用背景,对PFSP的优化调度不仅可以提高生产效率,还可以提高资源的利用率,多年来已经得到广泛而深入的研究并取得了较好的成果。
如今,混合群体优化算法成为一个关注较高的研究方向,这些研究促使求解PFSP问题进入新的阶段。文献[2]针对粒子群早熟的缺点,提出了一种结合迭代贪婪算法的混合粒子群算法,使用迭代贪婪算法对停滞的粒子和全局最优粒子进行变异,然后利用模拟退火思想概率接受新值,跳出局部极值。文献[3]基于模糊化处理和蜂群寻优的特点,提出模糊人工蜂群算法,将模糊输入输出机制引入算法保持蜜源访问概率的动态更新,避免陷入局部极值。文献[4]提出混合离散人工蜂群算法,加入离散差分进化与变邻域搜索策略,雇佣蜂阶段接受新个体采用模拟退火的概率突跳机制,使用锦标赛方法进行选择,在侦察蜂阶段对锦标赛选择的个体执行破坏重建操作。文献[5]提出一种混合的迭代局部搜索算法,将基于超启发式的变邻域下降算法嵌入迭代局部搜索算法中。文献[6]提出一种结合集束搜索的迭代贪婪算法,首先利用基于构建启发式的快速集束搜索来评估部分工件序列,然后将构建启发式算法用于产生初始解。文献[7]结合NEH启发式构造初始解的策略提出一种混合的猴群算法,初始种群的生成采用随机方式和基于NEH的方式,同时利用SPV规则完成工件编码。
上述研究通过实验证明了群体优化算法对于求解PFSP问题的有效性。为了进一步提高求解质量,文中研究了新兴的化学反应优化(chemical-reaction optimization,CRO)与水波优化(water wave optimization,WWO),提出一种混合的水波化学反应优化(wave chemical reaction optimization,WCRO)算法,同时引入迭代贪婪、路径重连等策略,力求混合算法在局部搜索、全局搜索以及收敛速度上均具有良好的表现,最后通过与其他算法进行实验测试对比证明该算法的可行性。
1 PFSP问题的数学描述
PFSP问题一般描述为n个工件需要在m台机器上加工,每个工件需要经过m道工序;每道工序要求不同的机器;n个工件在m台机器上的加工顺序相同;每个工件在每台机器上的加工时间表示为pij(i为第i个工件,j为第j台加工机器)。记π={π1,π2,…,πn}为所有工件的一个排列,C(πi,j)为工件πi在机器j的加工完成时间,则各工件在每台机器上的加工完成时间的数学模型如下:
C(π1,1)=pπ1,1
(1)
C(πi,1)=C(πi-1,1)+pπi,1i=2,3,…,n
(2)
C(π1,j)=C(π1,j-1)+pπ1,jj=2,3,…,m
(3)
C(πi,j)=max{C(πi-1,j),C(πi,j-1)}+pπi,j
i=2,3,…,n;j=2,3,…,m
(4)
式1表示第1个工件在第1台机器上的完工时间;式2表示第i个工件在第1台机器上的完工时间;式3表示第1个工件在第j台机器上的完工时间;式4表示第i个工件在第j台机器上的完工时间。
加工的总完工时间Cmax(π)计算如下:
Cmax(π)=C(πn,m)
(5)
PFSP问题的目标是寻找一个工件排列序列π*使得Cmax(π*)最小,如式6所示:
Cmax(π*)≤Cmax(πn,m)
(6)
2 求解PFSP问题的WCRO算法
2.1 PFSP问题编码
文中PFSP问题的解采用离散编码方式,每个工件用一个整数代表,工件从0开始标记,{0,1,…,n-1}为n个工件标记,如n=5的一种工件序列为{2,3,1,4,0}。
在WCRO算法中,每个工件序列对应种群中个体的结构,工件序列的完工时间对应个体的适应度值。
2.2 WCRO算法概述
文中将CRO算法与WWO算法混合,提出了一种新的混合水波化学反应优化算法(WCRO),算法框架如图1所示。

图1 WCRO算法框架
WCRO算法首先初始化种群,然后进入由CRO与WWO协作完成的迭代优化阶段,化学反应优化针对种群个体,即随机选择种群中的个体进行化学反应优化操作,水波优化则针对整个群体进行优化操作,迭代完成后输出最优解。
2.3 基于NEH_GRASP初始化种群
为了得到多个质量较高且多样性的初始解,采用文献[8]提出的基于NEH的贪婪随机自适应搜索算法(NEH_GRASP)。NEH_GRASP算法在构造解时,首先对每一个候选元素赋予一个贪婪函数值,将每个工件在所有机器上加工完成的时间作为贪婪函数值,并按照从大到小进行排序;其次,将排在前面的候选元素选入到约束候选表中;然后,从约束候选表中随机选择一个元素构造初始解;重复上述操作直至初始解中包含所有的工件。NEH_GRASP算法一次生成一个初始解,经过多次执行可获得多个质量较高且多样性的初始解。
2.4 化学反应优化
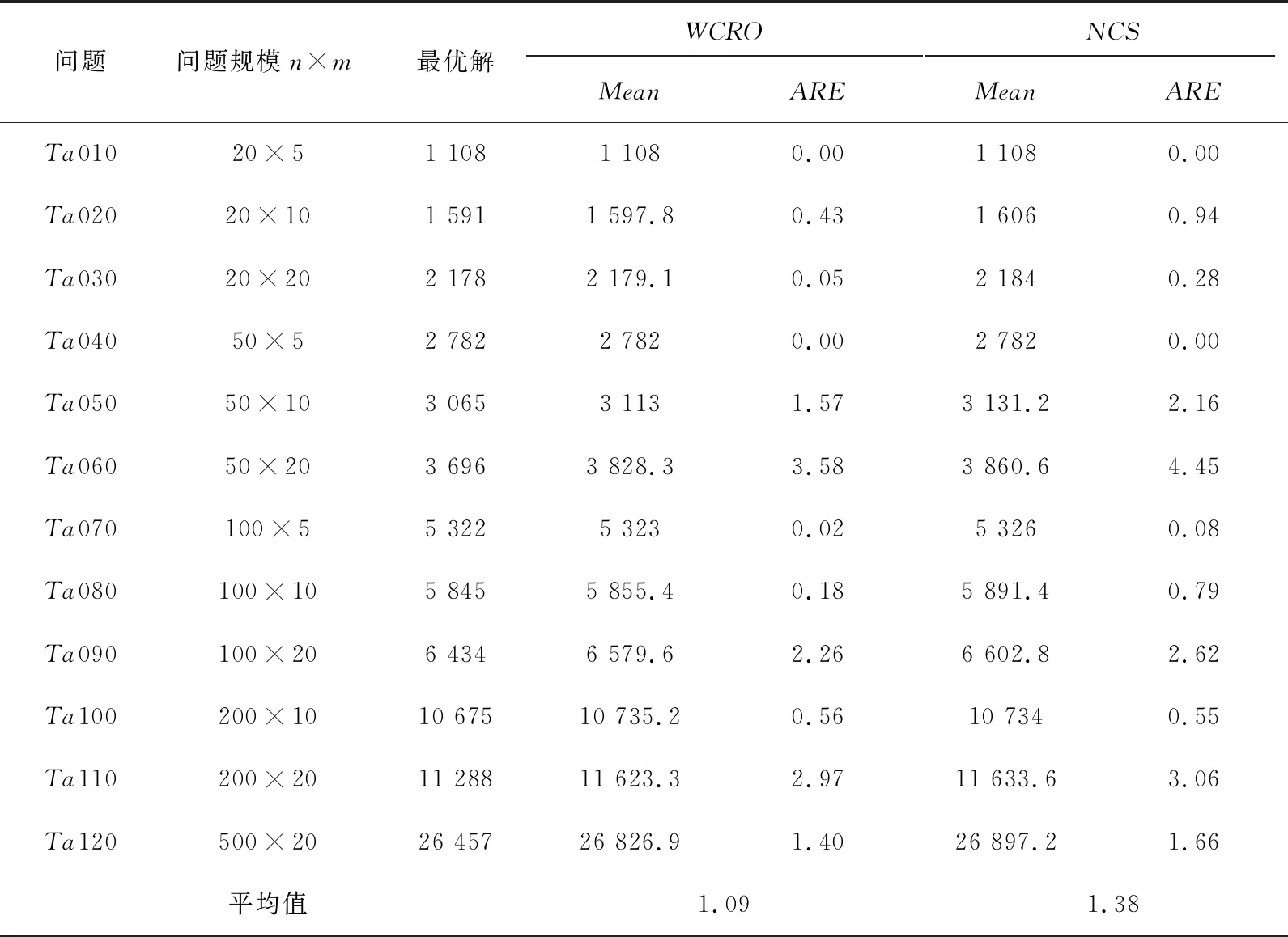
CRO算法是一种模拟化学反应变化的群体优化算法[9]。反应中的分子通过不断进行撞墙、分解、互撞以及合成四种反应实现能量的转化以寻求更低的势能。CRO算法具有保持种群多样性、全局搜索能力好的优点,而分解与合成反应在整个算法中的作用不明显[10-11],因此只保留撞墙和互撞反应。分子动能随反应的进行逐渐降低,则反应所需条件也愈加难以满足,为了使反应持续进行,在反应前加入分子动能是否过低的判断,当KE 2.4.1 撞 墙 撞墙反应指单个分子与容器壁碰撞后分子结构发生改变的过程,使得分子对应的解突变,防止算法陷入局部最优,文中采用基于随机互换方式实现撞墙操作。首先随机选择一个分子,然后针对分子的结构即工件序列,随机选择两个不同的位置工件进行交换,如图2所示。 图2 撞墙反应的分子结构变化 2.4.2 互 撞 互撞反应是指两个分子间发生碰撞后分子结构发生变化,发生碰撞的两个分子间进行信息交换,文中采用基于位置的交叉操作(position-based crossover,PBX)。随机选择两个分子,记互撞前后分子对应的工件序列分别为A、B和A'、B'。首先,确定保留信息的长度d且d∈[1,n];其次,随机选择A中的几个位置,将选中位置的工件直接保留到A'序列中对应的位置;最后,先在B中找出第一步选中的工件在本序列中的位置,再将其余工件按顺序放入A'中的空缺位置,如图3所示。 图3 分子碰撞反应的结构变化 B'生成的规则与A'相同,先从B中随机选择保留的工件,再从A中选择剩余工件补充空缺位置。 WWO算法是一种以浅水波理论为基础,通过模拟水波的传播、碎浪、折射操作在搜索空间中进行寻优的新兴元启发式优化算法[12-13]。 WWO算法用于求解连续优化问题,而文中求解PFSP问题采用了离散的编码方式,因此,需要设计离散的水波优化算法的求解问题,同时引入迭代贪婪、路径重连、淘汰机制来改善算法的局部搜索能力和收敛的速度。 离散WWO算法包括四个阶段:传播、折射、碎浪以及淘汰劣解。算法对每个水波执行传播操作,传播后的水波适应度值、波长、波高发生改变。适应度值的变化情况决定是否执行碎浪操作,波高的变化情况决定是否行进行折射或淘汰劣解操作。记工件序列πi为第i个水波,λi为波长,hi为波高。 2.5.1 传 播 水波的波长决定传播范围,适应度越好其波长越小,传播操作的搜索空间也越小。迭代贪婪(iterated greedy,IG)算法[14]通过在原始解上进行破环、构造操作来获得一个更优质的解,以该算法作为传播操作算子。 破坏操作选择d个工件并从原始序列π中移除,π被分成两部分:πd包含d个工件,πr包含n-d个工件。构造操作从πd中依次选择工件尝试插入πr中所有可能位置,选择一个使πr适应度最好的位置。 记操作完成后的水波为π',如果π'适应度更好,替换原来的π,否则原水波波高减1。DWWO算法中波长决定IG算法中破坏长度d,即d=λi,每次迭代波长发生如下改变: (7) c2=Cworst-Cbest (8) λi=λmax-λmin·e-c1/(c2+ε) (9) 其中,λmax、λmin分别为最长波长与最短波长;Cmax(πi)为当前水波的适应度;Cworst、Cbest分别为当前最优解与最差解的适应度;ε=0.001避免出现除数为0的情况。 2.5.2 折 射 当水波经过传播后波高减小为0时,进行折射。利用路径重连(path relinking,PR)完成折射使当前水波πi保持向最优水波π*的学习性。文中采用基于交换的PR算法,通过交换工件位使起始解向目标解靠拢,此过程会产生部分中间解,选择适应度最好的中间解作为PR算法的结果。 2.5.3 碎 浪 如果传播后的水波的适应度比当前最优解更好,对水波πi执行碎浪操作,此操作能进一步对最优解的附近范围搜索。以基于插入的局部搜索算法完成碎浪操作,首先,随机生成一个具有n个工件的序列π',令π作为每次操作的结果;其次,依次遍历π'中的工件,并在当前水波πi中找到对应的工件并插入所有可能插入的位置,找到一个适应度最好的工件序π'';然后将π''与当前解π进行比较,如果更优则用π''替换π。 2.5.4 淘汰劣解 淘汰劣解是一种概率性的接受较差解的操作,引入此操作有助于加快收敛速度。如果当前水波πi传播后得到的工件序列π'比原来更差,水波高度减1后高度变为0时,根据rand<α(α为算法参数,rand是0到1之间的随机数)条件决定是否淘汰群体中适应度最差的水波,如果满足淘汰条件,将π'替换群体中最差水波,否则舍弃π'。 基于上述WCRO算法的框架设计,并且针对化学反应算法和离散水波优化算法给出的具体实现,WCRO具体程序流程设计如下:初始阶段以NEH_GRASP算法生成高质量、多样性的种群,然后进入迭代优化阶段,包括执行两种分子碰撞的化学反应优化和混合搜索策略的离散水波优化,在水波优化进行深度局部寻优前先以化学反应优化执行全局搜索,防止陷入局部最优。 伪代码如下: 1:基于NEH_GRASP算法初始化种群 2:While (迭代停止条件未满足) 3:If(rand(0,1)≥MoleColl) 4:随机选择一个分子m执行撞墙反应 5:Else 6:随机选择两个分子m1、m2执行互撞反应 7:End if 8:Fori=1:PopSize 12:End if 14:Else 15:hi=hi-1 16:If(hi==0) 17:对πi执行折射操作 18:hi=hmax 19:Else 20:If(rand(0,1)<α)淘汰劣解 21:End if 22:End if 23:End if 24:根据式7~9更新波长λi 25:End for 26:End while 借助Eclipse开发平台,使用Java语言实现求解PFSP问题的WCRO算法,程序运行环境为Windows 10 64位操作系统、主频3.4 G的Intel Core i3系列CPU、4G DDR3内存。实验测试采用Taillard[15]提出的120组基准测试案列。 WCRO算法涉及如下几个重要参数:最大迭代次数MaxIteration、群体规模PopSize、初始动能InitialKE、动能损失率KELossRate、单双分子反应决定因子MoleColl、低动能阈值LowKE、初始波高hmax、最大波长λmax、最小波长λmin、淘汰劣解决定因子α。参考肖华军等[16]有关CRO算法的研究以及Zhao[17]等有关DWWO算法的研究,对WCRO算法的参数设置如表1所示。 表1 WCRO算法参数取值 需要注意的是,在500×20的数据规模中,存在不同的解的完工时间差距较大的情况,太小的分子动能大规模问题中难以保证化学反应成功进行,因此在500×20规模的案例中,将参数InitialKE和LowKE分别设置为2 000和200,以此保证算法能够在所有测试案例中发挥作用。 实验结果的对比以两种比较标准为例:平均误差率(average error rate,ARE)和平均相对百分偏差(average relative percentage deviation,ARPD),算法针对每个案例独立运行10次。 公式如下: (10) (11) 其中,mean、best分别表示算法所求得的平均值和最优值;opt为目前已知该案例的最优值。 为了完成性能测试,选取近些年较新的算法:新布谷鸟算法(NCS)[18]、免疫遗传算法(VacGA)[19]、改进NEH算法(NEHLJP1)[20]与文中算法进行对比。对比结果如表2和表3所示。 表2 WCRO、NCS算法的ARE结果对比 表3 WCRO、VacGA、NEHLJP1算法的ARPD结果对比 由表2可知,文中算法除了问题Ta100的求解结果比NCS算法稍有不足外,对其余问题的求解结果均优于NCS算法。从表3中数据可以看出,文中算法对于求解Taillard所有问题得到的结果与最优解的误差最小,与VacGA算法和NEHLJP1算法相比寻优性能更好。 基于CRO与WWO算法提出一种新的WCRO算法。使用NEH_GRASP算法生成高质量、多样性的种群,保留CRO中两种分子碰撞完成化学反应优化,设计离散型WWO算法并引入迭代贪婪、路径重连、淘汰机制,以CRO与DWWO协作完成算法的主要优化过程。 通过实验对比证明WCRO算法求解PFSP问题的可行性。未来可以将WCRO算法应用于TSP、作业车间调度、混合流水车间调度等其他组合优化问题中,以进一步证明该算法的有效性。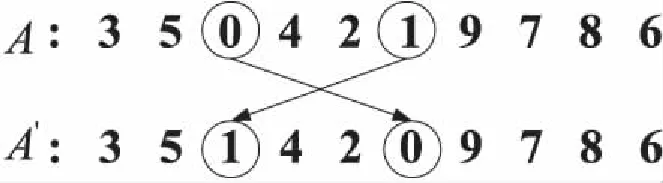
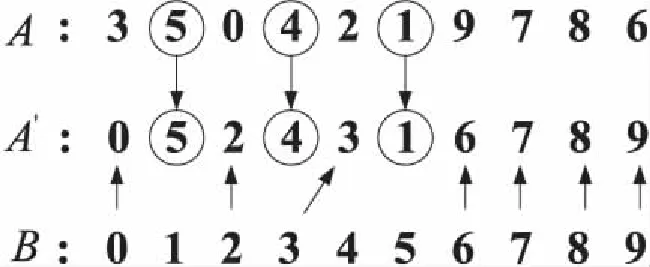
2.5 水波优化
2.6 WCRO算法设计
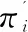

3 实验结果与分析
3.1 参数设置
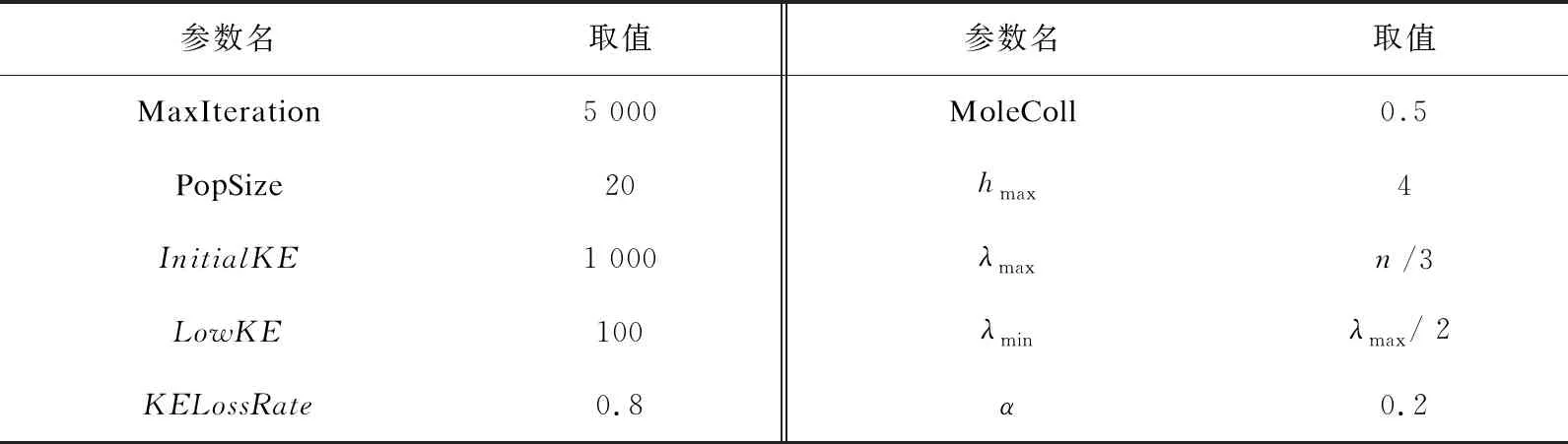
3.2 基准实例测试

4 结束语

