基于最小超球面密度的孤立点检测算法
冯 宇,苑易伟
(1.长安大学 电子与控制工程学院,陕西 西安 710064;2.西安理工大学 自动化与信息工程学院,陕西 西安 710048)
0 引 言
孤立点也被称作离群点或异常点,是指数据中不符合一般规律或明显偏离其他数据的数据。在数据挖掘研究领域,孤立点检测是一个重要的研究方向,其任务是通过算法寻找与大部分数据有着不同属性或含义的少量数据[1]。一方面,在数据预处理阶段发现并剔除这些数据,可以降低孤立点对数据挖掘结果的负面影响;另一方面,罕见的数据不一定是无用的数据,可能蕴含更大的研究价值,通过研究这些数据,会发现一些新的知识[2]。孤立点检测技术已经广泛应用于工业控制、网络安全、电子商务等各个领域[3-4]。
1 相关研究
孤立点检测算法大致可以分为四类,分别为基于统计、基于聚类、基于距离和基于密度的算法。基于统计的孤立点检测算法需要已知数据集的统计学分布规律[5-6],并且应明确孤立点不服从这种分布规律。然而实际中孤立点的分布规律往往并不清楚,与此同时,结构复杂的高维数据集会明显减弱这类算法的效果。基于聚类的孤立点检测算法是通过聚类分析将数据划分为若干个簇,并给定阈值,小于设定阈值的簇即视为孤立点[7]。这类算法在聚类过程中就能检测孤立点,但其检测的效果与簇形成的质量密切相关[8]。基于距离的孤立点检测算法需要计算每个对象与其近邻的距离,并且认为孤立点与其近邻的距离比正常数据远。这类算法应用简单,并且其有效性得到了充分的论证[9],但如果距离参数选取不合适,算法的效果会变得很不理想[10]。基于密度的孤立点检测算法根据数据的局部孤立程度来寻找孤立点,该思路更符合孤立点定义,因此基于密度的孤立点检测算法近年来发展迅速[11-12]。
2 关键技术
文中提出一种基于最小超球面密度的孤立点检测算法(minimum hyper sphere density,MHSD),在介绍算法之前,需对相关的定义和概念进行阐述。
2.1 相关定义
定义1:给定正整数n,一个n维球面是n+1维空间中距离某个点为R的所有点的集合。
特别地,一个0维球面是长度为R的线段的两个端点,一个1维球面是半径为R的圆,一个2维球面是半径为R的球体的面。维数大于2的球面称为超球面。最小球是包含对象p的k近邻所有超球中半径R最小的球面,p不一定是球心。
定义2:NNk(p)是对象p的k近邻序列,RNNk(p)是k近邻中包含p的所有对象,即反近邻。
以图1为例介绍RNNk(p)的构造方法。假设数据集A={p,q1,q2,q3,q4,q5,},当k=3时,NNk(p)={q1,q2,q3,q4},NNk(q1)={p,q2,q4},NNk(q2)={p,q1,q3},NNk(q3)={q1,q2,q5},NNk(q4)={p,q1,q2,q5},NNk(q5)={q1,q2,q3}。则根据定义2,p的RNNk(p)为{q1,q2,q4},同样也能得到其他对象的RNNk。显然,NNk(p)与RNNk(p)不一定相等。
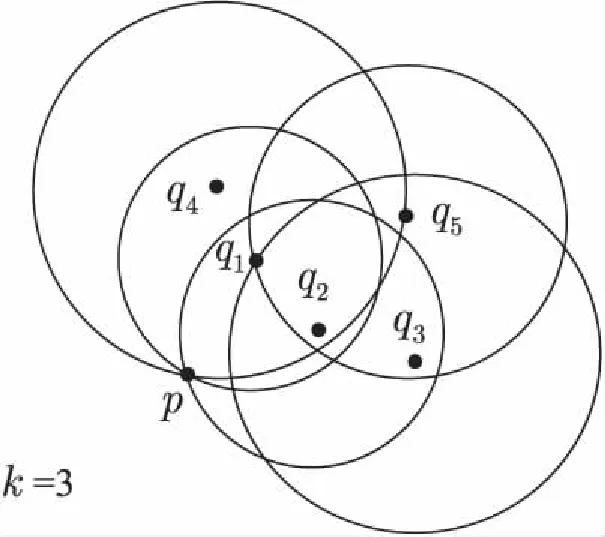
图1 反近邻构造方法示意
定义3:对于给定的正整数k,对象p的有效近邻定义为p的k近邻对象的k近邻中包含p的所有对象,即:ENP(p)=NNk(p)∩RNNk(p),ENP(p)可能为空集。
以图2为例介绍ENP(p)的构造方法。图中数据集D={a,b,c,d,e,f,g,h,i,j,k},当k=4时,d的k近邻NNk(d)={e,g,h,j},反近邻RNNk(d)={e,j};g的k近邻NNk(g)={e,f,h,i},反近邻RNNk(g)={e,f,h,i,k}。则d和g的有效近邻分别为ENPk(d)={e,j}和ENPk(g)={e,f,h,i}。

图2 有效近邻构造示意
根据上述定义,文中对最小超球面密度的定义为:
定义4:对象p的最小超球面密度是p的有效k近邻个数与最小超球面半径R的比值,即
(1)
其中,|ENP(p)|为有效近邻的个数。
2.2 算法描述
文中算法首先计算所有数据的有效k近邻,然后根据k近邻中的数据和对象p的距离从小到大排列,得到对象的最近近邻序列,通过计算对象p与有效k近邻中的最小超球面密度差来计算对象p的密度背离程度,最后根据有效k近邻中的所有数据的密度背离程度计算对象p的孤立程度。算法具体描述如下:
步骤1:计算每两个数据间的距离,并找到所有数据的k近邻。
步骤2:构建每个数据的近邻序列NNS。
设NNS(p)的初始值是{p},每次迭代把NNk(p)中距离p最小的对象加入到NNS(p)中,当NNk(p)中所有对象都加入到NNS(p)时,迭代结束。
步骤3:根据定义4计算所有数据的最小超球面密度。
步骤4:计算每两个数据的最小超球面密度差:
Δspden(x,y)=|spden(x)-spden(y)|
(2)
且Δspden(x,y)=Δspden(y,x)。
步骤5:根据最小超球面密度差,计算对象的最近近邻序列的密度背离程度(NDD)。
(3)
其中,r=|NNk(p)|。
步骤6:计算每个数据的孤立程度。
(4)
该值越小,说明p的孤立程度越低;该值越大,说明p越有可能是孤立点。根据设定的阈值便可检测出孤立点。
3 实验结果与分析
3.1 检测人工数据集的孤立点
人工二维数据集如图3所示,数据集包含1 700个正常数据和7个孤立点。这1 700个正常数据分为一个由200个服从高斯分布的数据组成的低密度簇C1和三个由500个服从高斯分布的数据组成的高密度簇C2,C3和C4。7个孤立点的编号分别o1,o2,…,o7。
使用三种经典的孤立点检测算法与文中提出的MHSD方法进行检测结果比较,三种方法分别为局部离群因子算法(local outlier factor,LOF)、离群影响因子算法(influenced outlierness,INFLO)和密度相似邻域离群因子算法(density similarity neighbor based outlier factor,DSNOF)[13-15],各方法检测结果中孤立程度最高的7个点如表1所示。可以看出,INFLO无法检测出o1、o5、o6和o7,DSNOF无法检测出o4,LOF和MHSD均可检测出7个孤立点,MHSD每个孤立点的孤立程度比LOF更大,说明MHSD的检测效果最理想。

图3 人工数据集示意

表1 人工数据集孤立点检测结果
3.2 算法性能评估
引入precision(Pr),recall(Re)和rank power(RP)三个参数评估算法的性能[16]。Pr表示算法检测出的孤立点的孤立程度在孤立程度最大的m个数据中的比例,Re表示算法在检测出的孤立程度最大的m个数据中孤立点个数占孤立点总数的比例,RP表示算法检测出的n个孤立点在孤立程度最大的m个数据中所占的位置参数。三个参数的值越大,表明算法性能越好。
数据集1选用经典的皮马印第安人糖尿病数据集[17],该数据集分为两类,第一类包含500个数据,第二类包含268个数据。将第一类数据随机删除488个,得到一个随机分布的簇,作为此实验中的孤立点[18]。为了比较在不同参数选择下不同算法的效果,将近邻个数k选为数据的维数、数据量的5%和10%,即k的值选择为8、14和28。各个算法的性能评估结果如表2~表4所示,其中Nrc为算法检测出的孤立点个数。

表2 k=8时的算法性能评估结果

续表2

表3 k=14时的算法性能评估结果
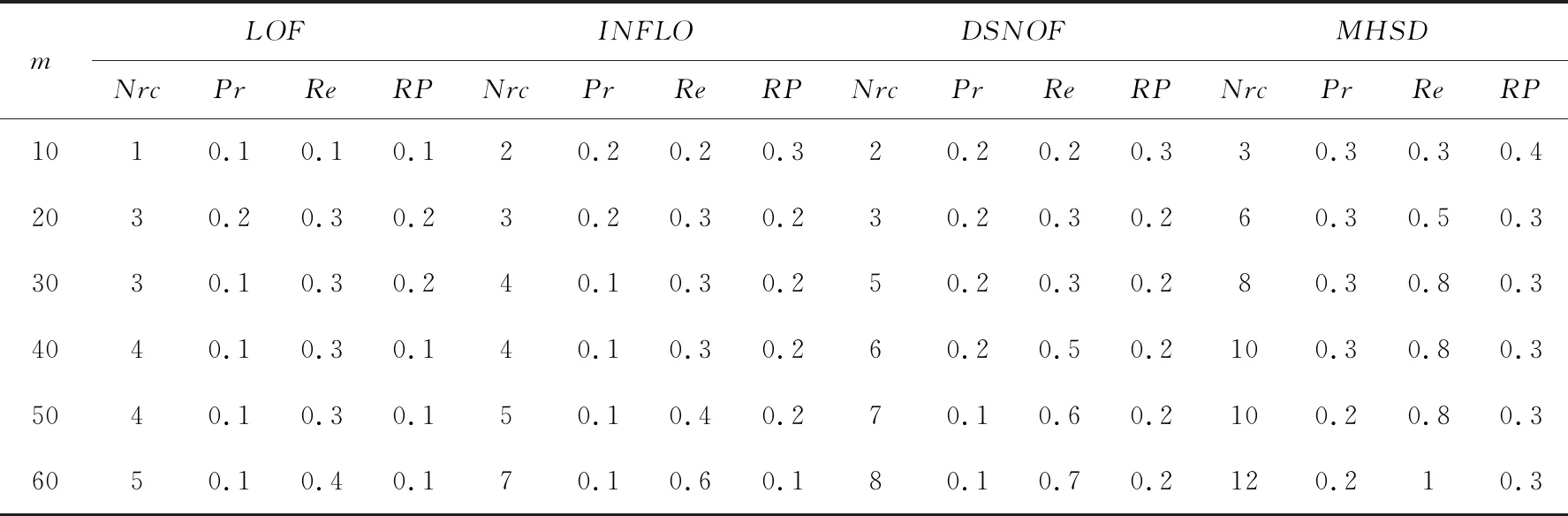
表4 k=28时的算法性能评估结果
当k=8时,在前10个孤立程度最大的数据中,只有MHSD能发现一个孤立点。随着m的增大,MHSD能够检测出的孤立点个数迅速增多,当m=90时,所有孤立点全被检测出来。此时LOF、INFLO和DSNOF分别检测出4、4、3个孤立点,MHSD的性能最好。当k=14时和k=28时,有类似的结果。真实数据集算法性能评估结果表明,MHSD算法随着k值的增大效果变好,并且优于LOF、INFLO和DSNOF。
数据集2选用本课题组在生物信息实验中实际测量的小鼠心脏窦房结场电位信号数据集,将在常温环境下(22±2℃)测量到的230个数据作为正常数据,从低温环境下(5±2℃)测量到的数据中取出10个作为孤立点,数据维度为30,取k=30。各个算法的性能评估结果如表5所示,MHSD的性能最优。
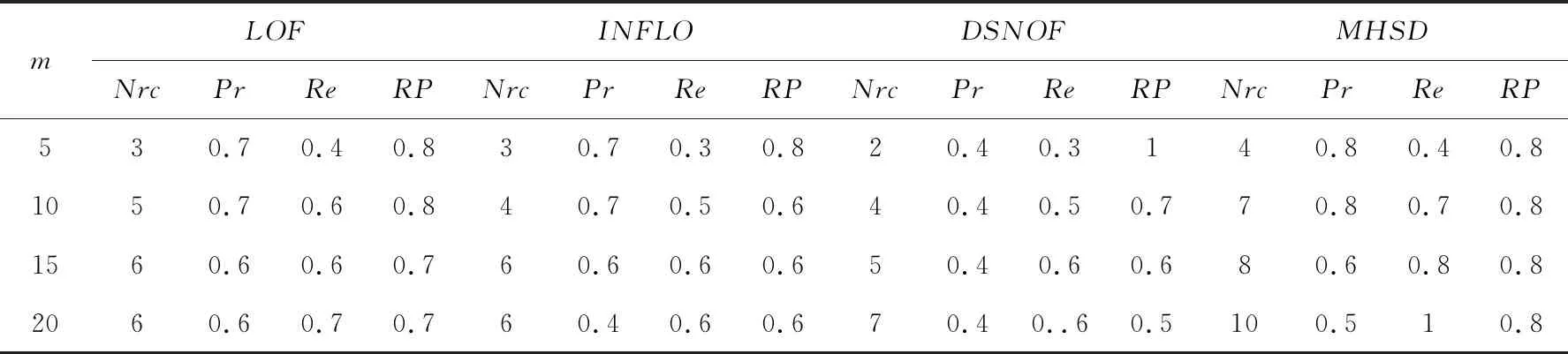
表5 使用生物信息数据集的算法性能评估结果
4 结束语
文中提出了一种基于最小超球面密度的孤立点检测算法,该算法通过找出对象数据的近邻序列,利用最小超球面密度差计算近邻序列密度背离程度,进而计算每个数据的孤立程度。使用人工数据集和真实数据集的检测结果表明,MHSD可以检测孤立点,且与经典的LOF、INFLO和DSNOF三种算法相比,MHSD的性能最优。

