STEMM视域下的初中数学“综合与实践”教学*
——以“反比例函数问题”为例
□黄 雄
(福建省厦门双十中学,福建厦门 361000)
一、问题的提出
近年来,起源于美国的STEM教育理念逐渐在我国被广泛传播.STEM是科学、技术、工程和数学英文的简称.STEM教育指在科学、技术、工程和数学领域的教和学,它是一种以项目学习、问题解决为导向的课程组织方式,通过项目探究和动手实践创造的方式学习[1].其宗旨是提升学生解决实际问题的综合能力和跨学科的思维能力,有利于学生问题意识、应用意识和创新意识及能力的培养.
STEM视域下初中数学“综合与实践”教学,要求学生从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,综合利用科学、工程、技术和数学的思想方法,求出结果并讨论结果的意义,这些内容的学习有助于学生初步形成模型思想,提高学生学习数学和应用数学的意识.
本文以人教版《数学》九年级下册第26章《反比例函数》数学活动2为素材,采用5E教学模式:情境吸引、模型探究、协作解释、成果展示和反馈评价,开展STEM视域下初中数学“综合与实践”教学研究.
二、教学设计与实施
(一)情境吸引(Circumstances Engage)
为各小组提供实验器材,多媒体展示引例:如图1,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O并将其吊起来.在中点O的左侧距离中点O25cm处挂一个重9.8N的物体,在中点O右侧用一个弹簧秤向下拉,使木杆处于水平状态.改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:N)有什么变化,并填写下表:
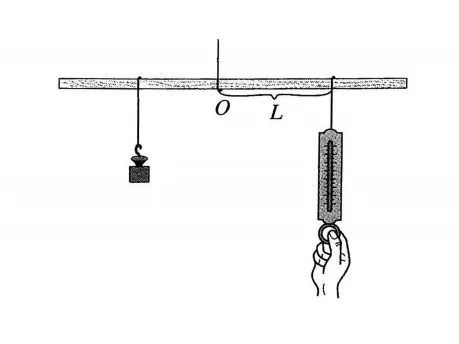
图1

L/cm F/N 5 10 15 20 25 30 35 40 45
以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.在坐标系中描出以上表中的数对为坐标的各点,并用平滑的曲线顺次连接这些点.
【学生活动】小组合作,合理分工,动手实践.
【设计意图】根据教师提供的实验器材,学生按以往的小组组合进行分组动手实践,有利于吸引并激发学生的学习兴趣,让学生在不知不觉中进入最佳状态的学习.
(二)模型探究(Models Explore)
应用希沃授课助手拍摄,投影学生1所作图象(见图2),同时,多媒体显示设问:这条曲线是反比例函数图象的一支吗?为什么?点(50,4.9)在这条曲线上吗?
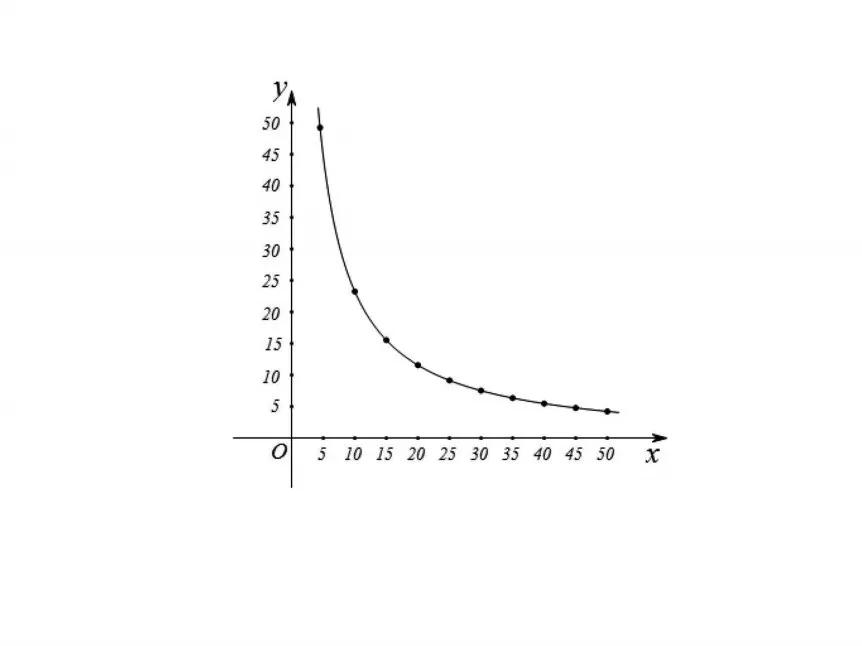
图2
【师生活动】
学生2:通过直观感知图象,我认为这条曲线是反比例函数图象的一支.
教师:你能说明原因吗?
学生2(略加思索整理):在物理中学过杠杆原理:阻力×阻力臂=动力×动力臂.结合已知条件,可以得到:25×9.8=F·L,从而由于L>0,所以该图象是反比例函数图象的一支.
教师:回答得非常好!你们小组在描点、连线的画图过程中,有没有要注意的问题和大家分享?
学生2:我们小组认为连线过程中要使用平滑的曲线,不要用折线连接.
教师:是的.除此之外,同学们是否注意到该图象是双曲线的一支,那么在画图过程中还需要注意什么细节?
学生3(补充):所画曲线都在第一象限内,图象不能与坐标轴相交.
教师:回答正确.点(50,4.9)在这条曲线上吗?
教师:同学们同意学生3的回答吗?
学生(齐声):同意.
【设计意图】本例来自物理学科,学生在物理课中已学过相关学科背景,具备一定的学科基础.通过本例教学,有助于学生体会数学与物理学科之间的联系,有利于培养学生的数学建模能力,在具体的情境中,从数学的角度发现问题、提出问题、分析问题和解决问题.
(三)协作解释(Coordinate Explain)
多媒体显示追问1:改变重物悬挂的位置,重复上述操作,所得曲线是否仍是反比例函数图象的一支?点(50,4.9)在新的曲线上吗?(说明:可以采用手持图形计算器HP39gs绘制图象)
【学生活动】小组合作,自由改变重物悬挂位置,动手实验,并用手持图形计算器HP39gs绘制图象.
【设计意图】以问题为载体,学生自主参与继续动手实践,合作探究,协作解释,契合STEM的教育理念.学生自由改变重物悬挂位置,保证实验结果的多样性和丰富性,有利于学生在众多实验结果中发现事物的辩证统一性.
在本环节教学过程中,学生应用信息技术,使用手持图形计算器HP39gs进行描点连线,可以更加精确、直观、形象地绘制反比例函数图象,体验应用信息技术解决问题的便捷.
多媒体显示追问2:所得反比例函数的图象中,是否存在两个图象相交的情形?为什么?
【师生活动】
学生4(小组代表):从所画的图形来看,不存在两个图象相交的情形.
教师:你能说明理由吗?
学生4:好像无法从正面得出结论.
教师:嗯,的确从正面很难证明,那有什么办法吗?
(片刻之后,少部分学生举手示意)
学生5:可以用反证法证明,先假设它们相交.
教师:请你和同学们分享你的想法.
教师:说得真好!请同学们按照学生5的思路,写出证明过程.
【设计意图】用数学思想方法解决问题,回归数学本质.教师在协作解释环节不急于抛出答案,而是由学生相互启发思考取长补短,最终实现问题的有效解决.
多媒体显示追问3:重9.8N的物体悬挂在中点O左侧距离中点O10cm处,若想使弹簧秤的示数不超过重物重量的2倍,则弹簧秤的用力位置至少应该在中点O右侧的什么位置?
【学生活动】小组合作探究,有困难的小组可以继续动手实验.
【设计意图】从表面上看,本追问是不等关系,但可以转化为相等关系解决.学生在相互协作解释中,仿照前几节课运用不等关系解决问题的方式,使问题得以解决.通过本追问,让学生应用数学知识解决实际问题,体验数学与物理学科的有机融合,从另一个侧面讨论实验结果的意义.
多媒体显示以下内容.头脑风暴:反比例函数不仅在现实世界中具有众多原型,而且具有广泛的应用.请你结合自己的生活与学习经历,举出生活中蕴含反比例函数关系的例子.
为保证头脑风暴活动的顺利进行,活动前教师可以向学生提供以下“头脑风暴活动指南”[2].
头脑风暴活动指南
进行头脑风暴活动时,以下做法是值得提倡的:
(1)记录下团队的各种想法.
(2)团队中的每个成员均要分享自己的想法.
(3)打破思维定式,欢迎各种具有创新性的奇思妙想.
(4)相互倾听、尊重和权衡,不要随意评价和质疑其他人的想法.
(5)尽可能多地提出自己的观点.
同时为了引导学生记录讨论的内容,并对团队其他成员的观点进行辩证的思考,可使用头脑风暴记录及评价表(见表1).

表1
【学生活动】小组合作探究,进行头脑风暴.
【设计意图】头脑风暴过程中讲究协作解释,学生通过发散思维,提出自己的想法,并学会倾听他人意见,加深对反比例函数在生活中应用的理解,进一步理解数学与科学的有机融合,为成果展示环节做好必要的准备.同时引导学生开展自评和互评,将反馈评价环节有机地结合在教学过程中.
(四)成果展示(Achievement Exhibit)
【师生活动】
学生6(小组代表):在使用剪刀的时候,被剪的物体放在剪刀口的不同位置,用力就有所不同.我们小组认为这是反比例函数在生活中的实际应用.
教师:同学们认为学生6的回答正确吗?如果正确,那么物理背景是什么?
学生:正确.物理背景是“杠杆原理”.
教师:大家回答得很好!
学生7(小组代表):我家台灯的亮度可以控制.其原理是:电压一定时,台灯功率P是电阻R的反比例函数.电阻越大,台灯的输出功率就越小,台灯就越暗.同理,电阻越小,台灯的输出功率就越大,台灯就越亮.
学生8(小组代表):受学生7小组的启发.我们小组认为:收音机的音量、电风扇的转速都由电器的输出功率决定.道理与台灯的亮度可以控制相仿.同样地,这是反比例函数在生活中的实际应用.
教师:非常好!刚才同学们所举的台灯亮度、收音机音量、电风扇转速都是反比例函数在实际生活中的应用.但它们都有前提条件:电压一定.
学生9(小组代表):物体运动的速度与所花时间成反比例关系.比如动车的速度比汽车快,所以动车所花时间就比汽车少.
教师:物体运动的速度与所花时间成反比例关系有前提条件吗?
学生9(有点不好意思):有,前提条件是:路程一定.
教师:同学们的表现非常棒!刚才发言的同学所举例子都很正确.用数学的眼光观察世界,你会发现数学无处不在.课后同学们可以进一步交流思考,体验反比例函数在实际生活中的诸多应用.
【设计意图】经历头脑风暴后,在成果展示环节,让学生充分展示小组研究的成果.在本环节中,学生再次体验从现实生活或具体情境中抽象出数学问题,有助于学生进一步形成模型思想,提高学习数学和应用数学的意识,实现STEM教育理念所提倡的科学、技术、工程和数学领域的教与学,提升学生跨学科的思维能力.
(五)反馈评价(Respond Evaluate)
学生填写“综合与实践”学习评价量表(表2),填写完毕后交给数学课代表.
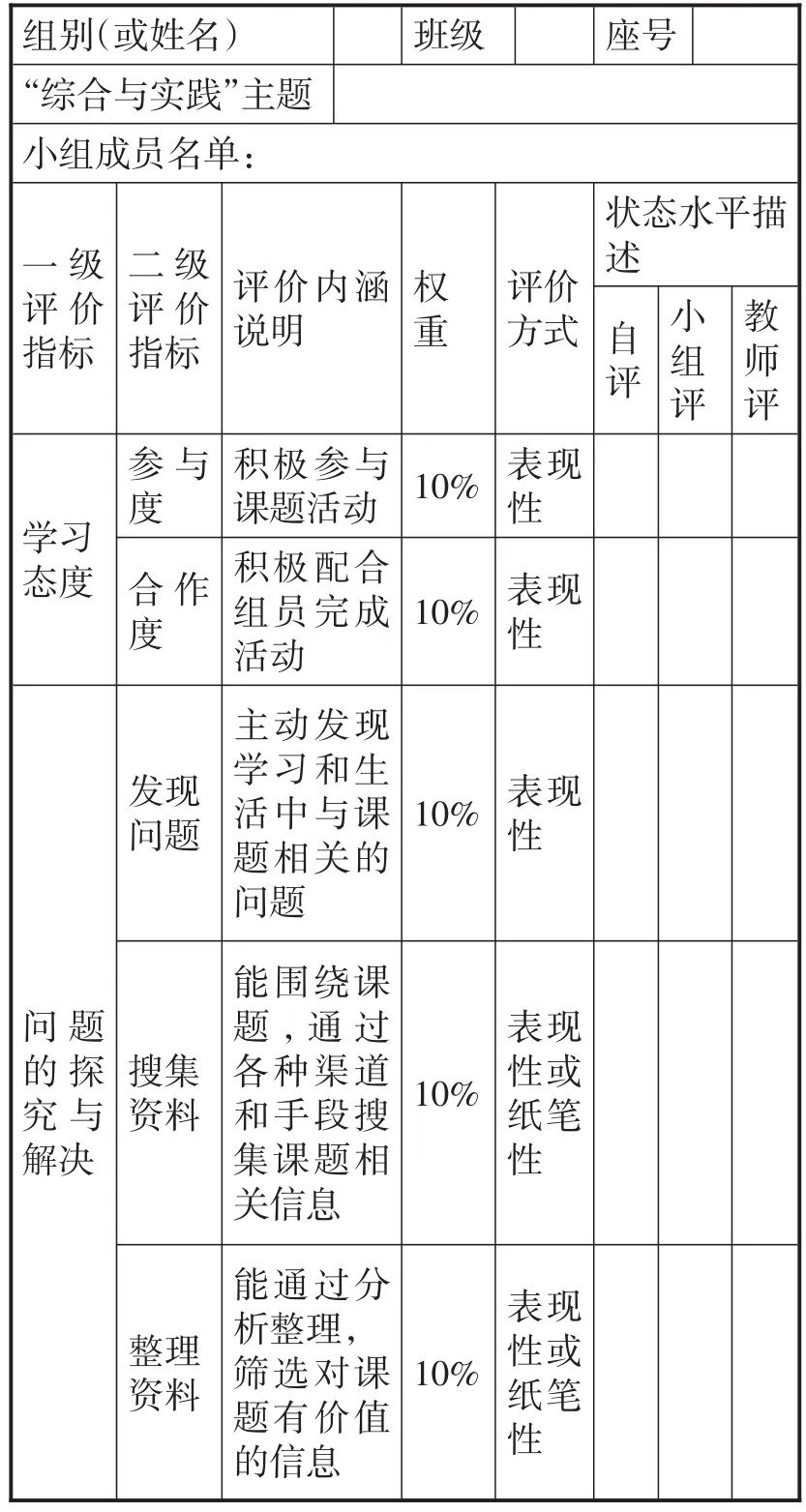
表2
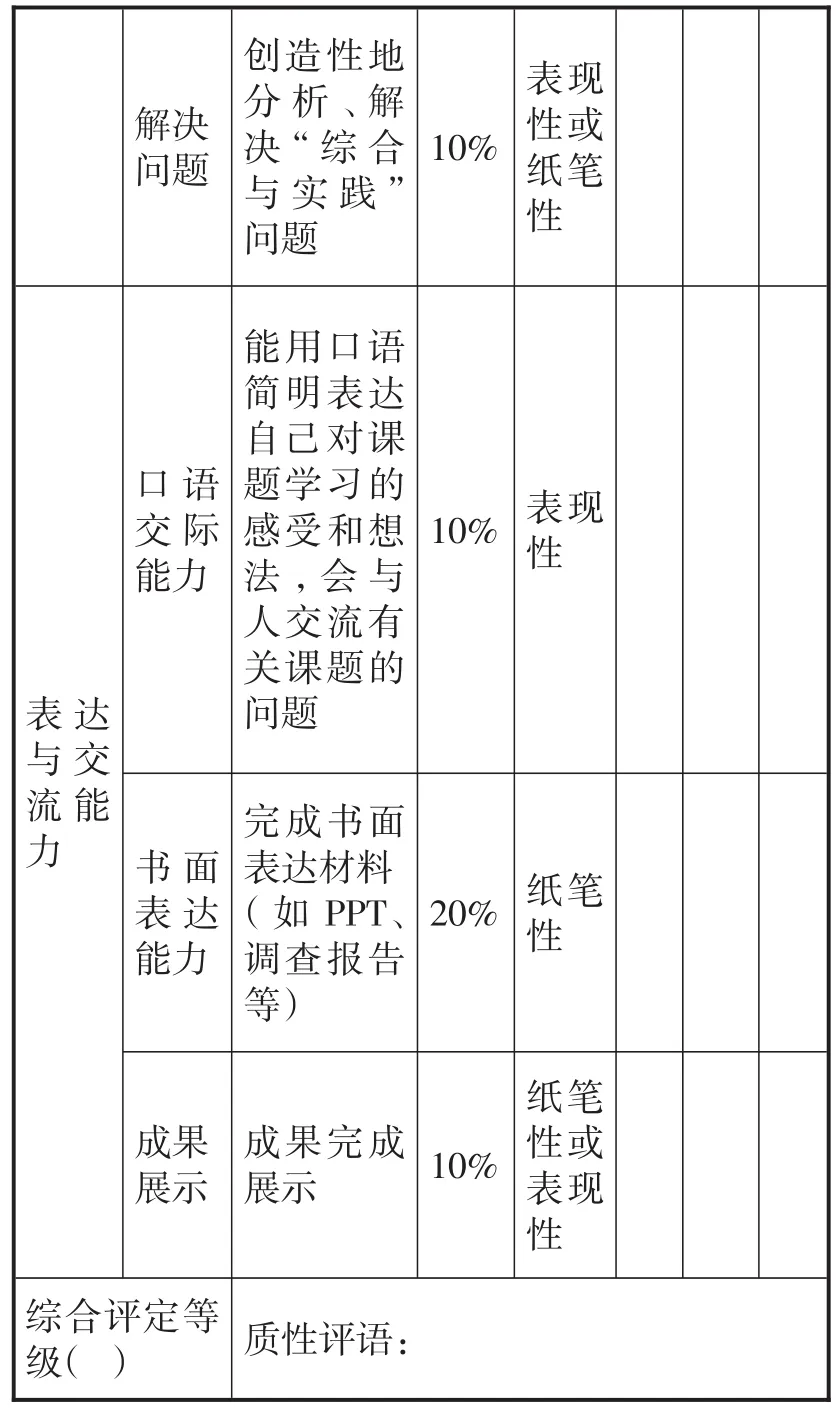
续表
【设计意图】学习评价量表可由学生在课后自主填写.反馈评价的设计意图主要是引导学生进行自评和生生互评,并结合教师评价,反思自己在课题学习过程中的得失,为今后的“综合与实践”课题学习积累经验.
课堂小结(略).
三、教学反思
从本节课例实施的过程和反馈效果来看,学生对“综合与实践”的学习持积极态度,每个学生都乐于与他人合作交流,能全过程参与,积累活动经验,展现思考过程,交流收获体会,激发创造潜能,促使学生“乐学”“爱学”“好学”,有效提高学生学习数学的兴趣.
基于STEM教育理念的初中数学“综合与实践”教学具有学科知识整合性的特点,它对教师的教学提出更高的要求,这对中学数学教师而言,是个巨大的挑战.教师只有在不断加强本专业知识积淀的同时,努力学习跨学科知识,掌握必要的STEM教学法知识,才能成为真正的内容传递者[3],成为STEM视域下初中数学“综合与实践”教学的推动者.
实施初中数学“综合与实践”课程有利于培养初中生的建模思想、应用意识、创新意识,这与STEM教育理念一致.STEM视域下采用“5E”教学模式,以项目学习、问题解决为导向开展初中数学“综合与实践”教学,融合物理、化学、生物、地理等学科开展科学研究,有助于学生进一步体会数学与其他学科之间的联系;有助于培养学生在具体的情境中,从数学的角度发现问题、提出问题、分析问题和解决问题的能力;提高学生数学知识的综合应用能力,更好地实现学以致用,更好地运用数学知识服务经济建设和社会各项事业发展.□◢

