一种面向稀疏数据的比率相似度计算方法

冯军美,冯晓毅,夏召强,彭进业,姚 娟

(1.西北工业大学 电子信息学院, 陕西 西安 710072;2.西北大学 信息科学与技术学院,陕西 西安 710127)

近年来,推荐系统[1]越来越多地应用在人们的日常生活中,根据用户的兴趣爱好、购买记录等信息为用户提供推荐。在推荐系统中,推荐算法在整个系统中是必不可少的。一般来讲,推荐算法分为4类:基于人口统计学的推荐[2]、基于内容的推荐[3]、协同过滤推荐[4]和混合推荐[5],其中,最常用的推荐算法是协同过滤推荐算法,且基于内存的推荐算法[6]和基于模型的推荐算法[7]是协同过滤推荐算法中的两个子类别。基于内存的推荐方法主要包括相似度计算和评分预测两个步骤。由于数据稀疏[8]和冷启动问题[9-10]在推荐系统中普遍存在,基于内存的协同过滤推荐方法中的数据稀疏问题是本文的研究重点。

目前,皮尔逊相关系数(Pearson correlation coefficient, PCC)和杰卡德系数(Jaccard)[6]是传统的基于内存的协同过滤推荐方法中比较常用的相似度计算方法。上述两种方法的相似度均通过用户之间共同评分项的评分数据来计算,但在稀疏的数据集上,共同评分项很少或者不存在,因此无法进行精准的推荐。针对这个问题,程伟杰等人[11]提出了一种利用用户的全部评分数据来提高推荐系统精度的方法,该方法借助动态权重将基于用户全部评分的相似度与皮尔逊相关系数进行混合,并根据混合后的相似度和最近邻的评分数据来预测用户对项目的评分大小。Guo等人[12]利用多种隐式反馈信息来解决推荐系统中的数据稀疏问题。Suryakant等人[13]考虑到传统的相似度计算方法存在数据稀疏问题,将3种相似度方法包括余弦相似度、杰卡德系数和平均散度进行线性组合来提高预测精度。

一种面向稀疏数据的基于用户的比率相似度计算方法在本文中提出。与现有的解决稀疏问题的推荐方法不同的是,该方法直接根据用户全部的评分数据来计算用户之间的相似度,根据相似度进行评分预测。解决了在稀疏数据的情况下传统的基于内存的协同过滤推荐算法无法计算相似度的问题,同时也提高了推荐算法的推荐精度。

1 传统的协同过滤推荐算法

基于用户的协同过滤推荐算法和基于项目的协同过滤推荐算法是基于内存的协同过滤推荐算法根据相似度计算对象的不同而划分的两种方法。本文把基于用户的协同过滤推荐算法作为主要的研究对象。

常用的相似度计算方法包括:PCC和Jaccard,上述两种方法均根据用户(项目)之间的共同评分项的评分数据进行相似度计算。两用户u和v之间的PCC的计算公式为

sim(u,v)PCC=

(1)

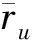
2 面向稀疏数据的协同过滤推荐算法

在实际的推荐系统中,用户之间的共同评分项通常很少或者不存在,评分数据集比较稀疏,采用传统的协同过滤推荐算法无法实现高精度的推荐。表1是用户User对电影Item的评分数据,从表可以看出,用户User 2和User 3之间只有一个共同评分项Item 5,User 1和User 2,User 1和User 3之间没有共同评分项的存在,在这种情况下,传统的相似度方法可以利用的数据很少或者没有,很难得到准确的相似度计算结果。因此,一种面向稀疏数据的比率相似度计算方法在本文中提出,该方法直接使用全部的评分数据进行相似度计算。

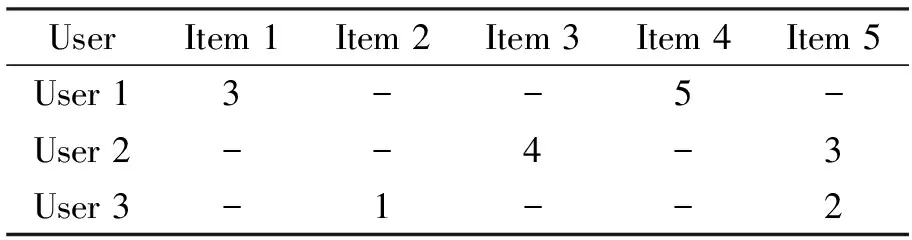
表1 用户对电影的评分Tab.1 Users′ ratings for the movies

2.1 面向稀疏数据的比率相似度计算方法

本文提出了一种面向稀疏数据的基于全部评分的比率相似度计算方法来解决传统的协同过滤推荐算法中相似度计算不足的问题。该方法定义用户u和用户v在所有项目上评分的集合Iu和Iv,用户u和v之间的相似度计算公式定义为

(2)

其中，|Iu|和|Iv|分别被用来表示用户u和用户v总的评分个数,用户u在所有评过分的项目上的第k个评分值用ru,k表示,用户v在所有评过分的项目上的第w个评分值用rv,w表示,min(ru,k,rv,w)函数返回ru,k和ru,w两者中的最小值,最大值通过max函数返回。从式(2)可以看出,本文提出的算法不依赖于共同评分项。

考虑到数据集中共同评分项的影响,对面向稀疏数据的比率相似度计算公式进行了修正,修正后的公式为

(3)

从式(3)可以看出,本文提出的相似度计算方法充分利用了用户评分数据集中的全部评分信息,相似度计算不会受到数据稀疏度的影响。

2.2 评分预测方法

用户u对未评分项目i的预测评分pu,i采用式(4)[14]进行评分预测，

(4)

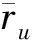
3 实验结果和分析

为了验证本文所提出的面向稀疏数据的比率相似度计算方法的有效性,实验在两个电影数据集MOVIELENS 100K和MOVIELENS 1M上进行,将文中所提方法与传统的基于用户的协同过滤方法进行了比较。

3.1 数据集

MOVIELENS 100K数据集包含100 000次评分, 这些评分是在1 682部电影上来自943个用户的匿名评价。 MOVIELENS 1M数据集包含1 000 209次评分,这些评分是在3 706部电影上来自6 040个用户的匿名评分,分值均为1～5。用户对电影的喜欢程度用分值的大小来表示,分值1表示用户非常不喜欢该电影,5表示非常喜欢。数据集的稀疏度不仅影响相似度计算的准确性,同时影响推荐系统的性能。本文所采用的两个数据集的稀疏度分别为93.7%和95.53%。

3.2 评价指标

由于本文所提方法以及用于对比实验的方法都是针对个性化推荐中的评分预测问题,因此，采用两个典型的预测精准度的度量指标:平均绝对误差(mean absolute error, MAE)[15]和均方根误差(rooted mean squared error, RMSE)[16],来度量算法的预测精度。MAE和RMSE越小,表示算法的预测误差越小,预测精度就会越高。MAE被用来估计预测值与实际值之间的平均偏差,计算公式为

(5)

其中,测试集中评分的集合用IT表示,pu,i被用来表示用户u在项目i上的预测评分值,ru,i被用来表示用户u对项目i的实际评分值。

RMSE反映了实际值与预测值之间的偏离程度,当预测值的误差较大时,RMSE比MAE更加敏感。RMSE用式(6)进行评估，

(6)

3.3 实验设置

为了验证本文提出的协同过滤算法在数据稀疏情况下的有效性,我们随机地移除了两个数据集中的一部分数据来构成稀疏数据集。在实验中,每个数据集上分别重构了7个稀疏度在97%～99.9%范围内,且步长为0.5%的稀疏数据集(稀疏度为99.9%的数据集除外),来验证稀疏度对本文所提出推荐算法的影响。对所有重构的稀疏数据集进行随机划分,取出其中的80%作为训练集,测试集采用剩余的20%。在接下来的实验中,本文提出的算法与PCC, Jaccard, CjacMD[13]和TMJ[17]这4种算法在性能上进行了比较。由于上述几种方法的性能同时受到稀疏度和最近邻的影响,所以,为了保证实验的准确性,本文需要确定上述4种方法的最佳最近邻数目,以排除最近邻的影响。

3.4 最近邻对精度的影响

本文选取在Movielens 100K数据集上重构的稀疏度为99.5%的稀疏数据集来验证最近邻对几种不同方法性能的影响。最近邻K设置为K∈[10,100]，步长为10。图1和图2分别展示了4种方法中MAE和RMSE随最近邻变化的实验结果。

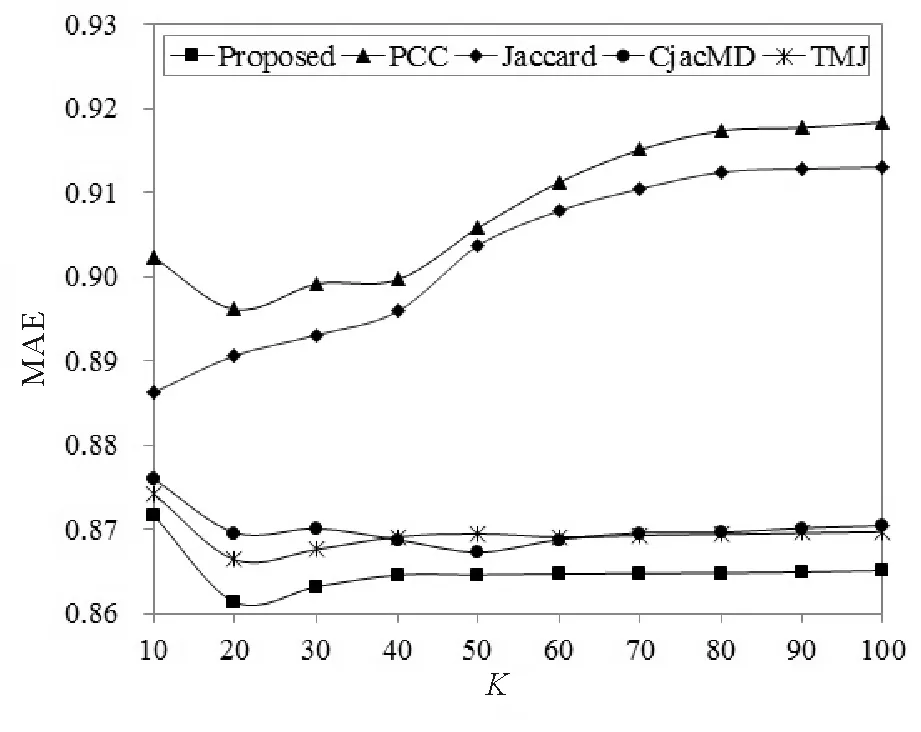
图1 最近邻对几种方法中MAE的影响Fig.1 Effect of nearest neighbors on MAE by several methods

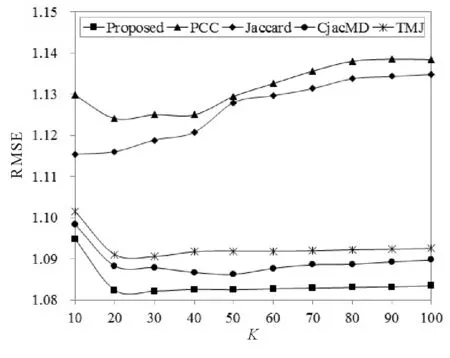
图2 最近邻对几种方法中RMSE的影响Fig.2 Effect of nearest neighbors on RMSE by several methods

从图1和图2中可以看出,最近邻对MAE和RMSE影响的变化趋势是一样的,本文提出的方法在整个最近邻范围内性能均最好,MAE和RMSE都比较低,当最近邻为20时,MAE和RMSE同时达到最低点。最近邻对本文提出的方法影响不是很大,在最近邻大于30以后，MAE和RMSE保持不变。PCC方法和Jaccard方法的性能相对较差,并且最近邻对Jaccard的影响比较大,随着最近邻的增加,性能逐渐变差。TMJ方法在最近邻为20时,两个指标均取到最小值,在最近邻大于40之后性能趋于稳定。CjacMD方法在最近邻大于60之后趋于稳定。实验结果说明,在整个最近邻范围内,本文提出的方法,PCC,Jaccard, CjacMD和TMJ方法在最近邻分别为20, 20, 10, 50和20时性能最好,两个指标均到达最低点。因此,在接下来的稀疏度实验中,本文提出的方法,PCC,Jaccard,CjacMD和TMJ上述5种方法的最近邻取值分别为20, 20, 10, 50, 20。

3.5 实验结果与讨论

在两个重构的不同稀疏度的稀疏数据集上来验证本文提出的面向稀疏数据的比率相似度计算方法的有效性。

图3和图4是在Movielens 100K上重构的7个不同稀疏度的数据集上得到的实验结果。图3和图4显示了本文提出的方法与PCC, Jaccard,CjacMD, TMJ方法在不同稀疏度条件下MAE和RMSE随着稀疏度变化的实验结果。可以看出,几种推荐方法的MAE和RMSE随着稀疏度的增加在不断变大。本文提出的方法在整个稀疏度实验范围内均取得了最小的MAE和RMSE,特别是在数据集稀疏度较高的情况下优势更大。PCC和Jaccard方法在整个稀疏度范围内MAE和RMSE值均比较高,性能较差。CjacMD和TMJ方法在稀疏度较低时和本文提出的方法性能比较接近,随着稀疏度的升高,性能逐渐变差。

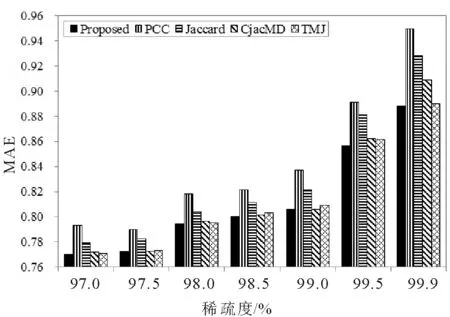
图3 Movielens 100K重构的数据集上稀疏度对几种MAE的影响Fig.3 Effects of sparsity on MAE of several methods on Movielens 100K reconstructed dataset

图4 Movielens 100K重构的数据集上稀疏度对几种方法RMSE的影响Fig.4 Effects of sparsity on RMSE of several methods on Movielens 100K reconstructed dataset

图5和图6是在Movielens 1M上重构的7个不同稀疏度的数据集上得到的实验结果。图5和图6显示了本文提出的方法与PCC, Jaccard,CjacMD,TMJ方法在不同稀疏度条件下的MAE和RMSE随着稀疏度变化的实验结果。可以看出,几种推荐方法的MAE和RMSE随着稀疏度的升高在不断地增加,性能也随之变差。本文提出的方法在整个稀疏度实验范围内的MAE和RMSE均较小,特别是在数据集稀疏度大于99%时优势更明显。PCC方法在整个稀疏度范围内MAE和RMSE值均比较高,性能也较差。Jaccard方法在稀疏度较低时MAE和RMSE值比较低,在稀疏度较高时性能一般。CjacMD方法的MAE和RMSE在整个稀疏度范围内均较低,性能仅次于本文所提出的方法。TMJ方法在整个稀疏度范围内优于传统的协同过滤算法。

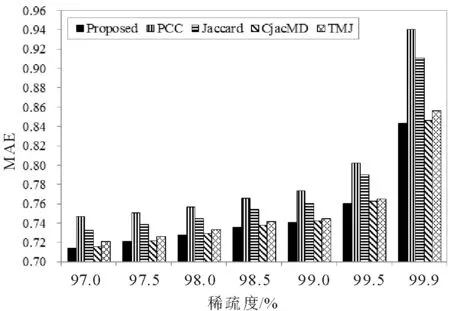
图5 Movielens 1M重构的数据集上稀疏度对几种方法MAE的影响Fig.5 Effects of sparsity on MAE of several methods on Movielens 1M reconstructed dataset

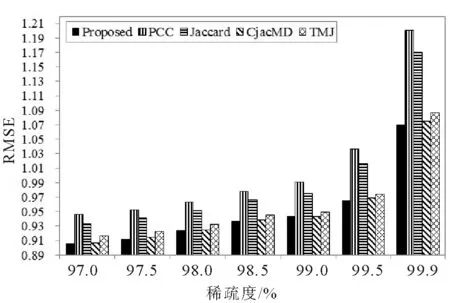
图6 Movielens 1M重构的数据集上稀疏度对几种方法RMSE的影响Fig.6 Effects of sparsity on RMSE of several methods on Movielens 1M reconstructed dataset

实验结果表明,PCC方法不适合对稀疏数据进行推荐,Jaccard, CjacMD和TMJ方法可应用在稀疏度较低的推荐系统,而本文提出的面向稀疏数据的比率相似度计算方法充分利用了全部的评分信息,且不依赖于共同评分项,在数据稀疏度较高的情况下也能保证系统的精度和性能。

4 结 论

本文提出了一种面向稀疏数据的比率相似度计算方法来提高推荐算法的预测精度和推荐系统的性能，主要贡献为:

1)本文提出的比率相似度计算方法是基于全部评分数据的,不同于传统的推荐方法的是,本文提出的算法不依赖于共同评分项。

2)充分利用全部评分数据,挖掘其中的有价值的信息,提高了推荐系统的推荐精度。

3)解决了传统的推荐算法对稀疏数据推荐精度不高甚至无法推荐的问题。

4)本文提出的相似度计算方法主要面向稀疏数据,尤其是稀疏度较高的数据,为进一步彻底解决稀疏问题和提高推荐精度提供了思路。

在接下来的工作中,我们将继续研究稀疏问题,并从隐式反馈信息入手,将其转化为显示信息来提高推荐精度。