《统天历》的岁实消长与气朔算法分析

滕艳辉，王鹏云，刘娅娅

(1.咸阳师范学院 数学与信息科学学院,陕西 咸阳 712000；2.西安财经学院 统计学院，陕西 西安 710100)

《统天历》是宋代极其特殊的一部历法,它首创“岁实消长术”,并放弃传统的上元积年,无论是对天文学的认识,还是对历算方法的改进,都达到了传统历法前所未有的高度。《统天历》在改变传统历法方面可谓大胆,虽然可能由于新法未能与新的观测完美匹配,导致其交食推算精度不高,饱受诟病,但它的思想方法直接启发了郭守敬《授时历》的制定。《授时历》很多方法自称沿用了《纪元历》之法,其实更直接的是使用了《统天历》之法。

《元史》记载《统天历》行用时间是庆元六年(1200AD)至开禧三年(1207AD),共8年[1]。但《宋史》载 “于是《开禧历》附《统天历》行用于世四十五年”[2][注]《元史历志》载《开禧历》行用44年,见《历代天文律历等志汇编》(9),3365页,自嘉定戊辰(1208)至淳佑辛亥(1251)应为44年。。那么,在《开禧历》行用期间,历官可能也使用《统天历》进行推算,与《开禧历》相互参照。这样,《统天历》真正使用的时间可能多达52年(1200AD—1251AD)。前人已经对《统天历》有过一定的研究,但更深入的探讨仍是必须的[3-8]。

1 《统天历》的岁实消长与积年算法

1.1 《统天历》的历元与积年

传统历法理想的上元时刻是甲子年、甲子日、日月五星同黄经同处升(降)交点并且是冬至日。这导致历法制定年到上元时刻的积年数非常庞大,有时甚至过亿。而《统天历》仅保证了上元时刻是甲子年和冬至日等少数几个条件,它的上元积年相比前历要小得多[1]。《统天历》上元距离宋绍熙五年(1194AD)为3830年,该年为甲子年,上元时刻为当年的冬至时刻。但这个冬至时刻并不在甲子日夜半,也不是近地点或远地点,还不是交点和日月合朔时刻。此时刻与上述几个天文起算点的关系如图1所示[8]。

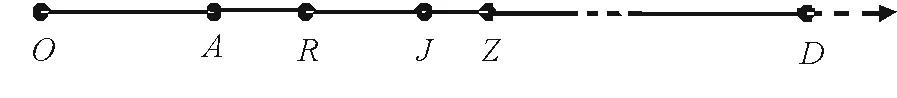
图1 《统天历》的上元时刻Fig.1 Epoch of Concord with Heaven System

图1中,我们令O表示上元时刻(冬至时刻),A点为上元后最近的甲子日夜半,R表示降交点时刻,J表示经朔时刻,Z表示近地点时刻,D是某年冬至时刻。在《统天历》中,OA=237811称为气差,表示上元时刻与甲子日夜半的距离,AJ=21704称为闰差,表示甲子日夜半到经朔点的距离,AR=80298称为交差,表示甲子日夜半到交点距离,AZ=188800称为转差,表示甲子日夜半到近地点的距离。这样,如果求冬至时刻就需要在OD上减去气差OA,求上元到某个朔的积月数,就要在依照上元时刻推得的基础上减去闰差AJ[8]。

1.2 岁实消长与《统天历》的回归年常数

由于地球自转长期变慢,这使得每一天的长度按原子时秒来衡量是在不断变长。如果以恒星日(即每一日的长度不变)来衡量,则回归年的长度则是在不断的变短,即回归年是一个古大今小的量。《统天历》不但意识到了这点,且给出了回归年变化的定量表达。《统天历》求天正冬至算法里面包含了这个表达,其术文称[2]:

置上元距所求年积算,以岁分乘之,减去气差,余为气泛积;以积算与距算相减,余为距差;以斗分差乘之,万约,为躔差。复以距差乘之,以减气泛积,余为气定积。满纪实去之,不满,如策法而一为大余,其大余命甲子,算外,即得日辰。

设《统天历》回归年常数为t=T/A,A为策法,Nn表示所求年距上元的积年数,该年回归年长度是tn,我们暂称之为回归年变量,N1194表示所求年至绍熙五年(1194AD)的积年数,则Δn=Nn-N1194=k,Δn在历法中称为距差。这样《统天历》距上n年的岁实消长数值可表示为

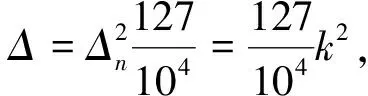
(1)

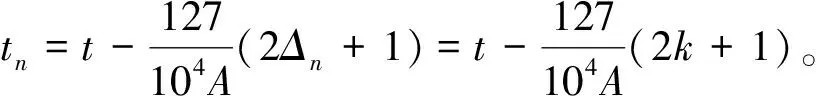
(2)

这样,可以得到任意年的回归年变量为

tn=365.d2424989147-0.0000021167(n-1194)

(3)

式中n表示儒略纪年。与文献[6]中的结果相比,这个结果更加精确,而文献[6]中则是近似值。因为1194年的回归年长度也不是365.2425日,而是要减去斗分差除以一万倍的策法。《中国天文年历》发布的回归年常数理论值为

tn=365.d24219878-0.0000000614(n-1900)。

(4)

可见《统天历》给的回归年常数过大,并且消长的幅度也过大。例如,《统天历》计算1900年回归年为365.24210045,与理论值相差0.0001日,不到10s;但1194年回归年的理论值为365.24224213,《统天历》回归年误差近4min。

2 《统天历》的气朔算法

2.1 求冬至时刻算法

《统天历》不使用传统的上元积年并首创消长法,受此影响,它气朔算法也与其他历法不同。设Δq为气差,根据其天正冬至术文,可得到其冬至时刻Tdz计算公式为

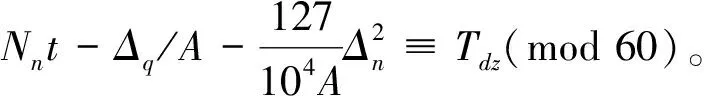
(5)

由于回归年长度自上元以来,逐渐减小,Nnt-Δq/A是依照1194年回归年计算得到的,称为气泛积。如果所求年在1194年以后,气泛积要比实际所求年到上元最近甲子日的时间长,就要减去这段时间岁实减少的累积值;反之,1194年以前,所求年到1194年的时间小于真实值,要加上累积值,而气泛积相应的还是要减去累积值,因此公式(5)中对于累积值都要用减号。《统天历》的真实的上元时刻应该在历法给定的上元前面。经计算,历法给定上元在甲子日前237811日分,合19.8175日,即上元是甲辰日15.21刻。如果按式(5)计算,上元的实际时刻为戊子日64.97刻。

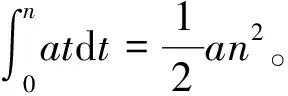
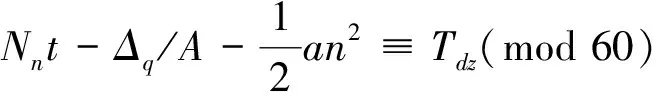
(6)

如果1194年冬至的时刻已知,其他年份的冬至时刻求起来更为方便,《统天历》在求冬至术文的小字部分给出这种方法方法。术文称[2]:

如求已,径以躔差加减岁余,距差乘之,纪实去之,余以减气积差二十【二】[注]原文为207489,我们重新计算1194年天正冬至,得227489日分,此处当改。万七千四百八十九,如策法而一,余同上法。

据术文,则有

Tdz=

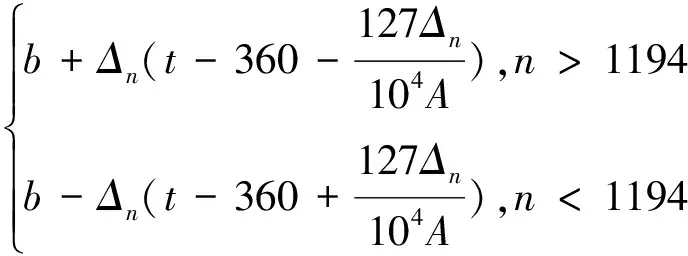
(7)

其中b就是1194年天正冬至时刻,Ab=207489为气积差。

对于上述两种形式,在符号的选择上,术文称“其加减躔差,乘积算,少如距算者加之,多如距算者减之;其加减气积差,即反用之”[2]。很显然,如果在1194年以后,计算的冬至时刻应该加入岁余的若干倍,但由于岁实为消,则实际的时间提前,用减;而1194年以前的情况是,要减去岁余的若干倍,此时,岁实为长,也应再减去消长的累积值,但此值又在此前计算,因而先加后减,于是得到上面两种形式[8]。

2.2 定朔算法

《统天历》“求天正经朔”算法称:

置天正冬至气定积,以闰差减之,满朔实去之,不满,为天正闰泛积余;用减气定积,余为天正十一月朔泛积;以百五乘距差,退位减之,为朔定积;满纪实去之,不满,如策法而一为大余,不尽为小余。其大余命甲子,算外,即得日辰。[2]

这样,设Δr为闰差,《统天历》的经朔Tpm可由下式求得:

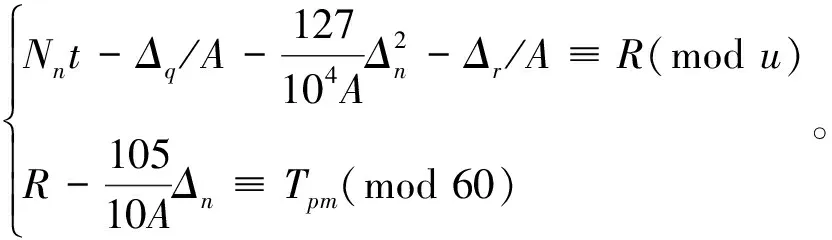
(8)

其术文的小字部分补充到:“积算少如距算者加之，无距算者，以泛为定。求交转准此”[2]。因距差[注]事实上,我们定义的距差是具有正负号的,《统天历》的距差都是正值,因此它要在小字中说明运算时正负号的取法。在1194年前为负,则式中取减号能保证实际计算时是加法。

《统天历》求日月改正数及求定朔的方法都与《纪元历》的相同,只是在求经朔入气与经朔入转时略有不同[9]。我们将会在后面的计算中详细说明这些。

2.3 《统天历》推算1191年冬至和定朔过程

为了更清楚展示《统天历》岁实消长计算气朔的方法,我们给出一个算例加以说明。元史载“绍熙二年辛亥十一月壬申四十七刻”[1]，这是在计算公元1191年12月15日的冬至。其计算过程如下所示。

其中3828×4382910-237811-0.1143=240581168.8857就是气定积。因不足1日时,当日是甲子日,则8日时为壬申日,得到冬至时刻是壬申日余5668.8857日分,合11时20分,约为47刻23分,与史载计算完全一致。

我们可以进一步计算该年的天正定朔时刻。闰差Δr=21704,朔实U=Au=354368,

其中321372.8857是天正闰泛积余,16777541668.8857-321372.8857=16777220296就是朔泛积。

天正经朔到冬至的实际距离是321372.8857+10.5×(-3)=321341.3857,相当于其他历法中的天正闰余。《统天历》一个平气长度为182621.25日分,321341.3857>182621.25,因此,经朔前面的最近的平气是小雪气,又2×182621.25-321341.3857=43901.1143=3×12000+7901.1143,于是得到经朔入小雪气,入3日小余7901.1143。查询每日日躔表[注]每日日躔表是根据《统天历》24气日躔表经过二次插值计算得到,具体算法参考文献[10]。,得其日损益率为32,脁朒积-1058。根据文献[10]中的算法,得其朔入气腓朒定数为

接下来求经朔时刻距离最近一个近点的的距离,由图1知,上元附近,近点的在经朔点后面,这样要在朔定积基础上减去这段距离即转差18880。可得

结果不足1日是为入转1日,结果21即朔入22日余6137.5日分,其日损益率为-215,胐朒积为5008。由此得到入转胐朒定数为[9-10]

定朔时刻就是经朔加入气入转胐朒定数,即

1194年天正定朔时刻是丙午日188.6061日分,合丙午日1刻57分。

3 《统天历》气朔计算的精度

我们完全按照《统天历》推算冬至和定朔的算法,利用Visual Basic 9.0编写了计算机程序,能够方便地计算出任意给定的定朔和冬至。这样,如果将其与真实的天象相比较,就可以得到《统天历》计算气朔的精度水平。据文献[11],日月改正数周期大约9年或112个朔望月,我们就选择《统天历》行用初年(1200AD)向前和向后各推9年,计算这18年(1192AD—1209AD)的定朔,然后与真实值比较,讨论其定朔计算精度。同时,我们又计算了公元1101—公元1300年的各年的冬至时刻,与真实值比较,得到了《统天历》冬至推算的精度。本文的气朔真实值取自《三千五百年历日天象》中“合朔满月表”和“分至八节表”中的数据[12]。《统天历》气朔计算精度的各项指标如表1所示。

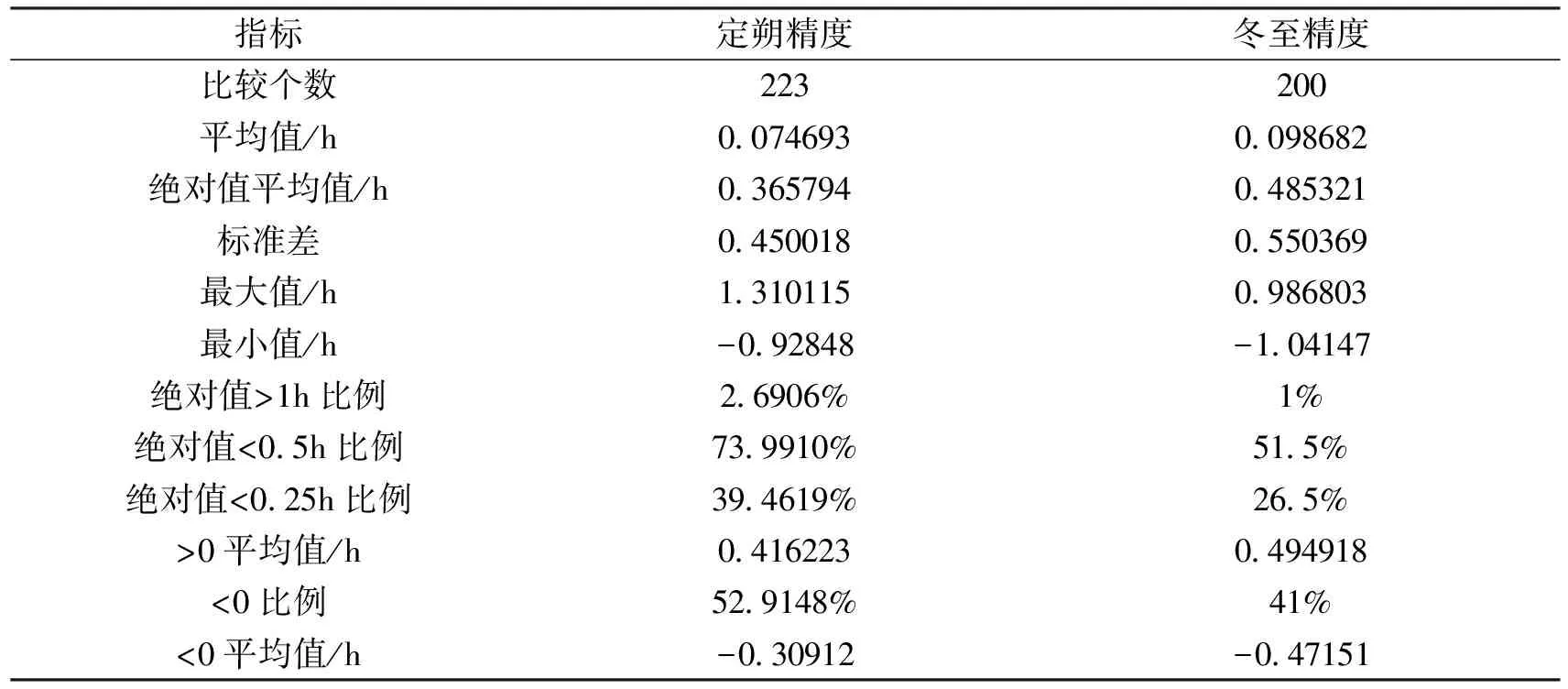
表1 《统天历》气朔计算精度Tab.1 Calculation accuracy of the true sun and the real new moon in Concord with Heaven System

《统天历》定朔误差平均值0.074693h,仅为4.5min,取绝对值为0.365794h,也仅为21.9min;反而算法相对容易,计算量较小的冬至时刻精度略低于定朔精度,冬至误差平均值为0.098682h,合5.9min,绝对值均值为0.485321h,合29.1min。最大误差方面定朔的为1.310115h,超过78min,而冬至的仅略大于1h;误差大于1h的,定朔有6次,而冬至仅为1次;其余的精度指标都是定朔的略优于冬至的。《统天历》定朔与冬至推算的精度分别如图2和图3所示。

图2 《统天历》定朔计算精度Fig.2 Accuracy of the real new moon

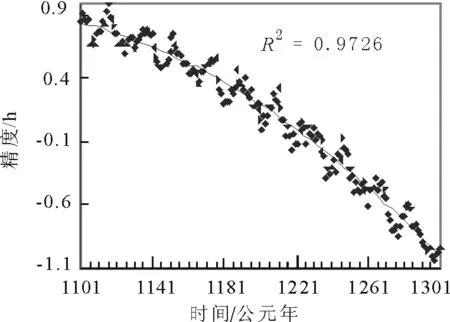
图3 《统天历》冬至计算精度Fig.3 Accuracy of the winter solstice

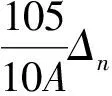
4 结 语

废传统积年并非《统天历》首创,唐曹士蒍《符天历》、五代马重绩《调元历》就曾有过尝试,它们的历元都在千年之内,但未得到官方的普遍认可。《纪元历》、《元嘉历》和《乙未元历》等历法也曾放弃了传统历法上元的条件,如上元不选择冬至,上元不在甲子日等。但《统天历》在这方面做的是最彻底的,它的上元仅仅保留了是冬至时刻,其余重要的天文点几乎都不与之重合,于是,杨忠辅又设立了各种“差”(闰差、气差等),保证历日天象的正常推算。这样,《统天历》的计算量降低了。我们的算例也能看到,里面出现的最大数值也仅达到11位,而传统上元积年的历法,推算时动辄15位16位,因为有些历法积年就达到8位9位。

《统天历》最重要的创新则在于它发现岁实消长,并给出定量描述。虽然早在刘洪和祖冲之时期,天文学家就讨论过岁差等问题,但真正明确回归年的变化,并完整应用在历法上,《统天历》是第一个。虽然由于这种方法与当时历家的思维及造历的原则不一致,并且行用几年后也出现了多次交食不验,但经过对其气朔的推算精度分析,我们发现其实《统天历》的推算精度还是可以的,冬至时刻的推算在百年内都能保证误差在1h以内,定朔的计算更是绝大多数稳定在0.5h左右。

《统天历》推算精度显然比不上其后的《开禧历》,在交食方面可能还不如前面的《淳熙历》和《会元历》,但这是两项空前创举第一次应用的结果,不成熟之处是很自然的。我们甚至可以设想下,如果能够给造历者更多的时间去测算和调整,他造出的第二部历法肯定会弥补推算精度上的缺憾。巧合的是,80年后,郭守敬正是继承了杨忠辅的方法,并重新测算了天文常数,他造出了传统历法的巅峰之作——《授时历》。