《五大历数书汇编》中的月亮中心差算法
——兼与6世纪之前中国月亮中心差算法比较
唐 泉,袁 敏
(西北大学 科学史高等研究院, 陕西 西安 710127)
汉魏六朝时期,印度天文学随佛教传入中国,此后一直延续至唐代而未中断。关于印度天文学在中国的流传与影响,江晓原和钮卫星进行过非常深入细致的研究,相关研究成果比较集中地收录在《天文西学东渐集》[1]和《西望梵天:汉译佛经中的天文学源流》[2]两部著作中。
公元6世纪中叶,北齐天文学家张子信经过多年天文观测,提出了太阳和行星的不均匀运动以及月亮视差会影响日食计算等一系列重大天文发现。隋代天文学家刘焯在制定《皇极历》时,率先考虑了张子信的重大天文发现,从而揭开了隋唐历法大变革的序幕。李约瑟指出,如果中国和印度天文学家并非独立发现了太阳的不均匀运动,那么张子信关于太阳不均匀运动的发现很有可能受到了印度天文学的影响[3]。钮卫星通过考察张子信的水星应见不见术,认为张子信隐居海岛时可能接触到某些印度天文学内容,并把它们吸收到中国传统天文学中的这种可能性是存在的[4]。
近年来,对古代中印数理天文学中的一些核心算法的比较研究,引起了学者的关注。例如,胡铁珠[5]对《大衍历》和《苏利亚历》行星算法的比较研究,曲安京[6]对古代中国和印度日月食食限算法的比较研究,唐泉和曲安京对古代中国和印度月亮视差理论的比较研究[7],袁敏[8]和刘丽芳[9]等人对中印晷影算法的比较研究,都值得关注。
伐罗诃密西罗(Varāhamihira)所著《五大历数书汇编》(Pacasiddhāntikā)是公元6世纪印度一部非常重要的数理天文学著作。该书所收录的5部天文学著作的概要,反映了公元6世纪以前印度本土天文学和传入印度的域外天文学的主要内容。《五大历数书汇编》一直受到科学史家的高度关注,自1889年至今,先后出现了3个影响较大的英文译本[10-12],相关研究也非常丰富[13-15]。然而,国内学者对《五大历数书汇编》的系统研究尚未全面展开,已有的零星研究,主要集中在太阳运动理论和行星运动理论[16-17]。
本文中,我们将详细考察《五大历数书汇编》中的月亮中心差算法,并与公元6世纪之前的《乾象历》、《景初历》和《元嘉历》等3部中国历法中的月亮中心差算法进行比较,进一步揭示中印数理天文学传统的多样性,为探讨公元6世纪之前中印数理天文学交流与传播线索提供相应的数理基础。
1 《五大历数书汇编》中的月亮中心差算法
《毗昙摩诃历数书》在《五大历数书汇编》中所占的篇幅非常小,原始的《毗昙摩诃历数书》所取近距历元为公元80年1月11日,其来源可能与巴比伦天文学有关[18]。原始的《沃西斯特历数书》成书于公元270年之前,其来源与希腊化的巴比伦天文学有关,但是收录在《五大历数书汇编》中的《沃西斯特历数书》,其历元已被改编为公元499年12月3日。原始的《罗马伽历数书》和《宝莉莎历数书》大约成书于公元3~4世纪,二者具有明显的希腊风格(文献[18],540~545页)。《太阳历数书》是5部著作中成书最晚的一部,根据《太阳历数书》所取近距历元为公元505年3月20日夜半,其成书年代应该略晚于这个时间。
在《五大历数书汇编》收录的五部著作中,只有《毗昙摩诃历数书》未涉及到月亮的不均匀运动,而其他4部著作均有涉及。《沃西斯特历数书》中的月亮不均匀运动算法比较初级,尚未完全将月亮中心差从月亮的平运动中分离出来,而《太阳历数书》、《宝莉莎历数书》和《罗马伽历数书》都是以公式或数值的形式给出了月亮中心差或某些区间内月亮平运动与真运动的差值,本文主要讨论这3部著作中的月亮中心差算法。
1.1 《太阳历数书》中的月亮中心差算法
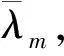
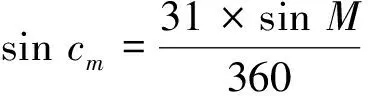
(1)
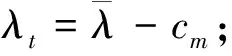
1.2 《宝莉莎历数书》中的月亮速度与中心差算法
《宝莉莎历数书》在《五大历数书汇编》中所占的篇幅较大,内容也相对比较完整。《宝莉莎历数书》将一个近点月长度均分为248padas,pada是一个比日更小的时间单位,它与日和近点月长度之间的关系为:1pada=1/9日=1/248近点月。由此可知《宝莉莎历数书》所取近点月长度为248/9≈27.555 6日,《沃西斯特历数书》采用了相同的近点月常数。
《宝莉莎历数书》将一个近点月从远地点作为起点等分为两半,若令p和p′分别表示月亮过远地点或近地点的时间,单位为pada,vm表示月亮每日实行速,单位为分,则月亮每日实行速度可以表示为以p或p′为自变量的函数(文献[12],45页):
(2)
《宝莉莎历数书》中的月亮中心差算法收录在《五大历数书汇编》Ⅲ.5~8节,共4段术文。T.S. Kuppanna Sastry和K.V. Sarma仅仅翻译了Ⅲ.5节,而未对Ⅲ.6~8节术文进行翻译。若设月亮的中心差为cm,单位为分,p和p′分别表示月亮过远地点或近地点的时间,单位为pada,则根据T.S. Kuppanna Sastry和K.V. Sarma对Ⅲ.5节的释读,月亮中心差cm可以表示为以p或p′为自变量的函数
cm=
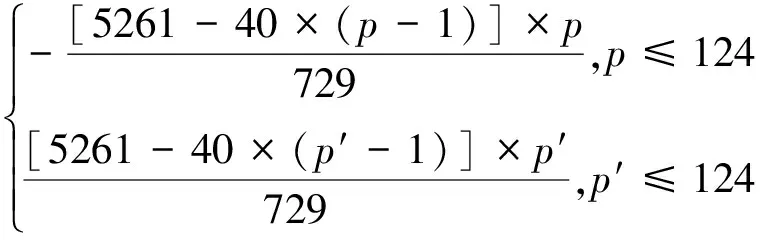
(3)
Otto Neugebauer和David Pingree对Ⅲ.5~8均给出了翻译,根据他们的翻译和释读,月亮中心差cm是以p为自变量的分段函数(文献[11],39~41页)。
若p≤120,
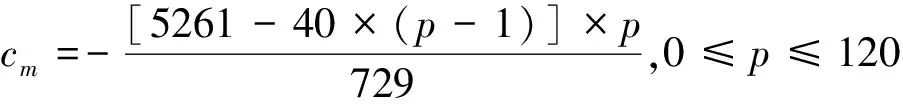
(4)
若p>120,令p′=p-120,
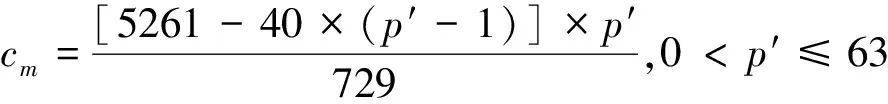
(5)
当p′>70时,令p″=p′-69,
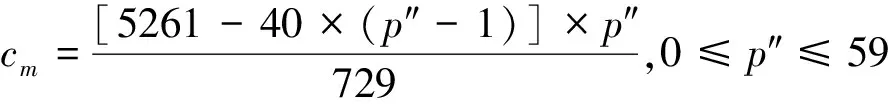
(6)
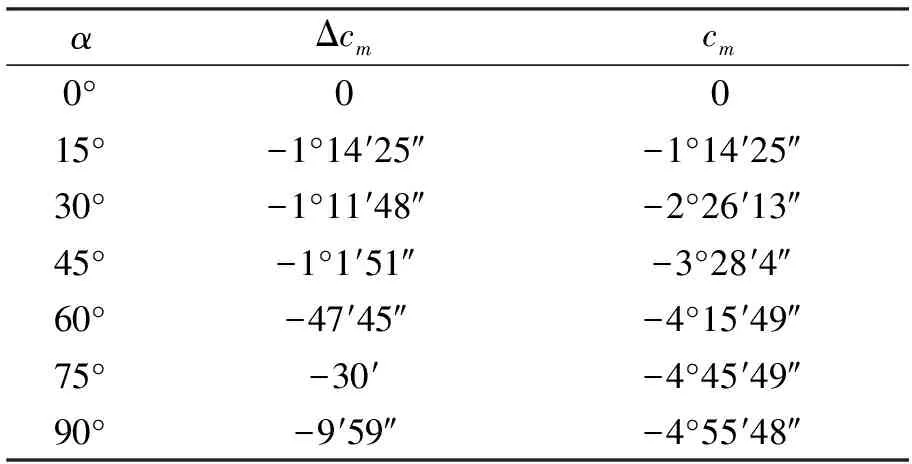
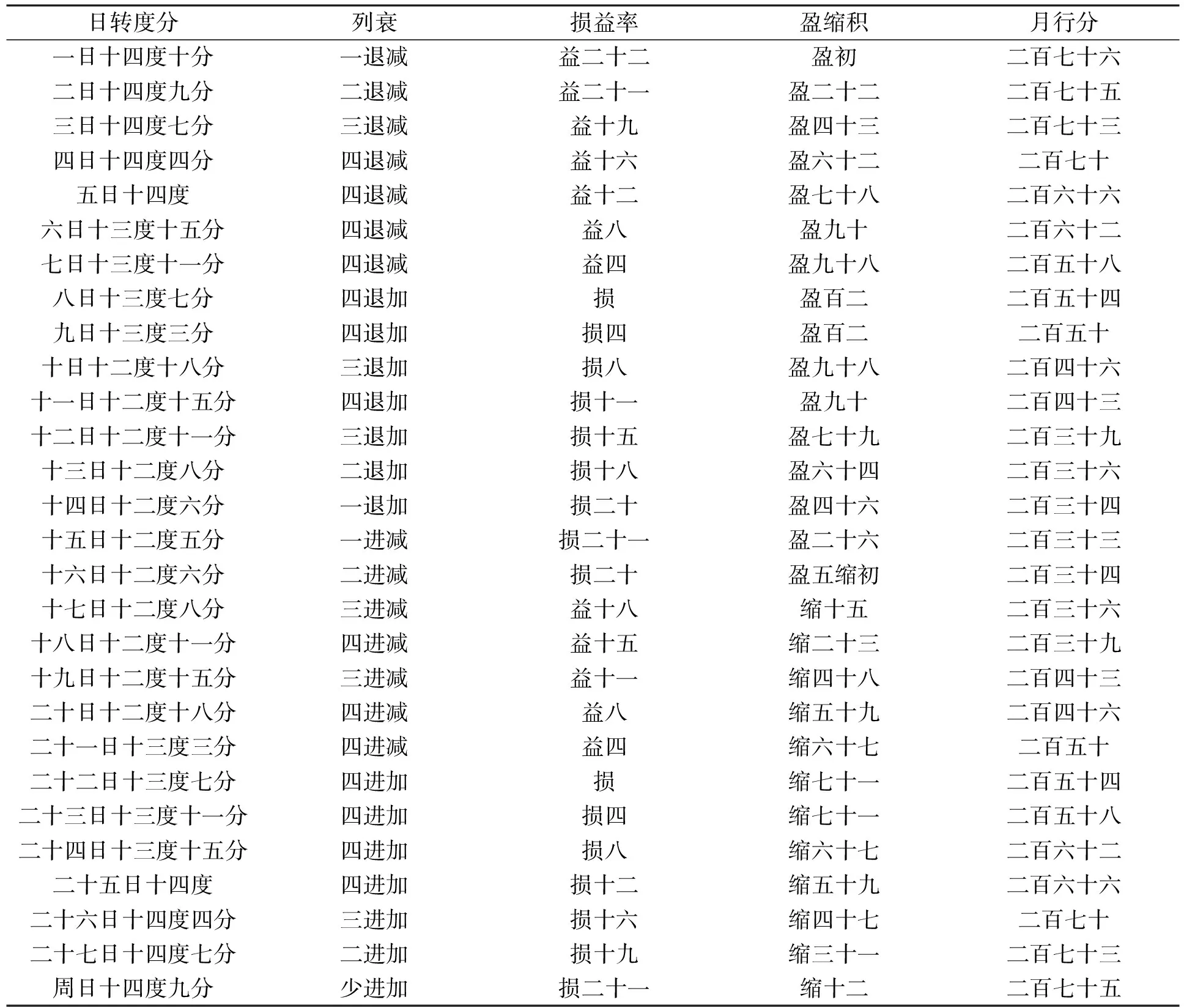
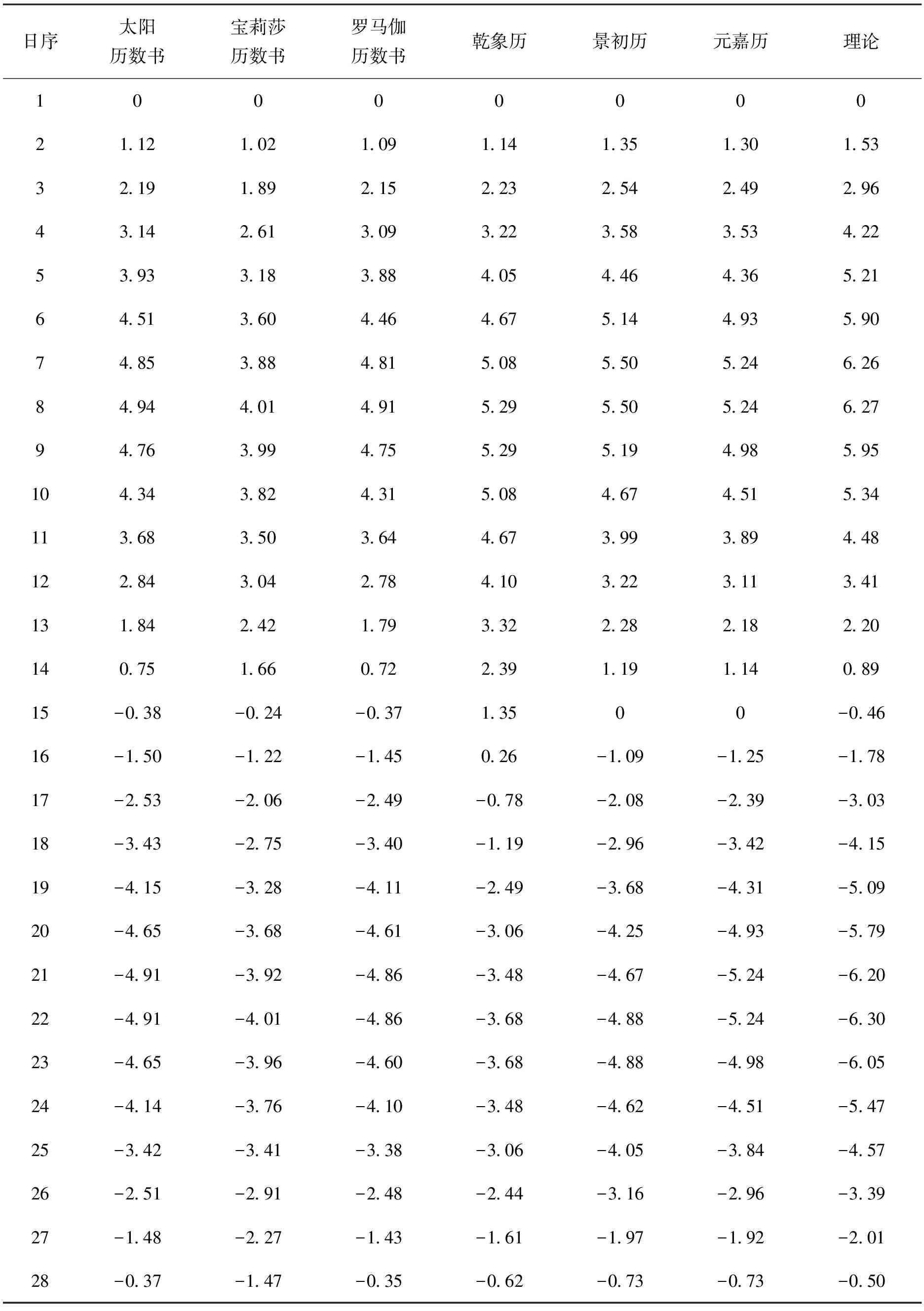
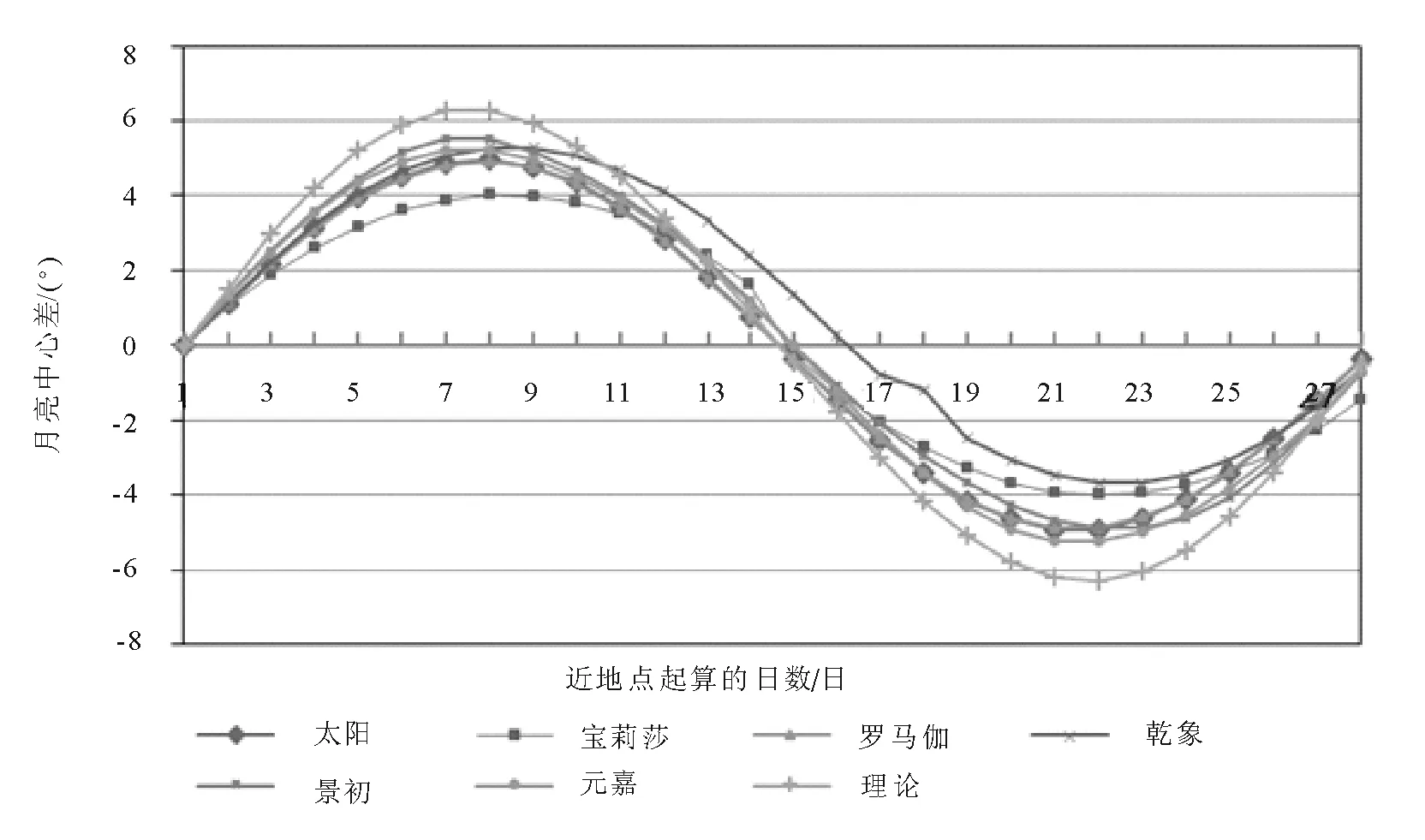
从式(4)~(6)看出,当63 《罗马伽历数书》中的月亮中心差也是从远地点起算的,但是与《太阳历数书》中基于本轮模型和三角函数的月亮中心差算法和《宝莉莎历数书》中以分段函数计算月亮中心差的算法不同,《罗马伽历数书》将一个近点月以远地点作为起点分为四个象限,并给出了第一象限内每隔15°月亮真运动和平运动的差值。若令α表示月亮的远点角,Δcm表示月亮实行度和平行度之差,cm表示月亮中心差,则根据《罗马伽历数书》术文(文献[12],183页),可以列出月亮在第一象限内Δcm和cm的数值,结果如表1。表1中Δcm数值系由《罗马伽历数书》直接给出,cm的数值系笔者累加Δcm数值得到。 表1 《罗马伽历数书》中的月亮中心差Tab.1 Lunar equation of center in the Romaka Siddhānta 表1给出了第一象限内每隔15°的Δcm的数值,其他各象限的数值可根据对称性求出。在第一象限和第四象限,Δcm均取负值,即月亮实行速小于月亮平行速,在第二和第三象限,Δcm均取正值,即月亮实行速大于月亮平行速。这里需要指出,Otto Neugebauer和David Pingree对表1中Δcm的数值给出了不同的释读,根据他们的释读,Δcm的数值依次为-1°14′,-1°11′,-1°2′,-48′,-25′和-6′,与表1中所列数据差距非常明显。此外,月亮在一个近点月内运行的距离略大于360°,但是《罗马伽历数书》则以360°入算。 我国古代对月亮运动的观测和研究非常重视,至迟在西汉,中国天文学家已发现月亮的迟疾运动。西汉末期,刘向(前77—前6年)提出月行九道术,此后九道术在西汉晚期和东汉非常流行,历法家利用九道术推算月亮迟疾运动和交食[20]。公元206年,天文学家刘洪在九道术的基础上,首次在其制定的《乾象历》中设计了月离表,对月亮的不均匀运动进行了较为科学的描述。《乾象历》之后的历法,除极个别历法直接以函数的形式给出月亮中心差算法之外,其他历法都设计了相应的月离表。 在隋代之前设计月离表的历法中,刘洪《乾象历》(206年)、杨伟《景初历》(237年)和何承天《元嘉历》(443年)是行用时间较长的3部历法,其中《乾象历》行用57年(223—280年),《景初历》行用114年(237—451年),《元嘉历》行用64年(445—509年)。《乾象历》术文保存在《晋书·律历志中》,为讨论方便,我们照录《乾象历》[21]月离表如下,见表2。 表2 《乾象历》中的月离表Tab.2 Lunar equation of center in the Supernal Emblem System 《乾象历》中的月离表奠定了中国古代月离表的基础,此后各历中月离表的内容虽然有所增损,但基本内容不变。《景初历》术文保存在《晋书·律历志下》和《宋书·律历志中》,其月离表(文献[21],1628~1629页)包括四栏,依次为“月行迟疾度”、“损益率”、“盈缩积分”和“月行分”,分别对应《乾象历》中“日转度分”、“损益率”、“盈缩积”和“月行分”等四栏内容。《元嘉历》术文保存在《宋书·律历志下》中,其月离表[23]包括六栏,第一栏为日序,其他各栏依次为“月行迟疾度”、“损益率”、“盈缩积分”、“列差”和“差法”,分别对应《乾象历》中“日转度分”、“损益率”、“盈缩积”和“月行分”。 通过分析《乾象历》、《景初历》和《元嘉历》等三部历法中月离表的结构与内容可知,这3部历法中与月亮中心差对应的栏目分别是“盈缩积”、“盈缩积分”和“盈缩积”。 由于太阳和大行星的摄动,使得月亮的运动变得非常复杂。月亮的真黄经和平黄经之间存在许多周期性差项,根据布朗的研究,这些差项主要包括中心差、出差、二均差、周年差和月角差,等等。在这些大的差项中,只有中心差系数以月亮的平近点角为引数,其他差项则与太阳和月亮的相对位置、太阳的位置、月亮距升交点的距离以及它们的组合有关[22]。为简化讨论,我们在本文中仅用月亮的中心差来刻画月亮平黄经和真黄经的差值。 根据天体力学知识,做椭圆运动的天体的中心差c可以表示为以近点角M为自变量的函数[24]: (7) 式(7)中e表示月亮轨道的偏心率,月亮轨道的偏心率并非一个常量,而是在1/15到1/23的范围内变化,其平均值为0.054 9,接近1/18[25]。若取偏心率至二乘方,则式(7)可简化为 (8) 利用式(8),我们可以对《太阳历数书》和《乾象历》等六部历法中的月亮中心差精度做一个初步的讨论。根据前面的讨论,在《五大历数书汇编》收录的三部著作中,月亮中心差均以远地点起算,而《乾象历》等3部中国历法中月亮中心差均以近地点起算。为方便比较,我们将3部印度历法中的月亮中心差均归算为以近地点为起点。 表3 《乾象历》等历法中的月亮中心差Tab.3 Lunar equation of center in the Supernal Emblem System and the other systems 根据表3中数据,可以绘出上述各部历法中月亮中心差变化曲线,如图1所示。 图1 《太阳历数书》等历法中的月亮中心差曲线Fig.1 Figure of luanr eauqtion of center in the Saura Siddhānta and the other systems 从表3和图1可以看出,上述六部历法中的月亮中心差曲线的振幅均小于理论曲线的振幅,而且在这六部历法中,《乾象历》月亮中心差曲线在远地点之前的振幅较大,在远地点之后的振幅较小,差别比较明显,《宝莉莎历数书》月亮中心差曲线振幅最小,其他四部历法中的月亮中心差曲线振幅接近月亮轨道偏心率取最小值时的振幅,其曲线形状与理论曲线形状也比较相似。 通过本文的讨论可以看到,在公元6世纪之前,中国和印度的天文学家都设计了月球中心差算法推求月球的真位置,月球中心差算法的设计,为提高月球位置计算精度提供了保障,从而为进一步计算日月食奠定了基础。通过比较《太阳历数书》等3部印度历法和《乾象历》等三部中国历法中的月亮中心差算法,我们可以得到如下认识: 1)中国和印度的月亮中心差算法具有不同的传统。《乾象历》等中国历法中的月离表以表格形式逐日给出了月亮在一个近点月内的各项数据,包括月亮每日实行速、月亮每日实行速与平行速差值以及月亮中心差等。月离表充分体现了中国数理天文学中数表的强大功能,是中国古代月亮运动理论中的基本表格。与中国历法中内容丰富的月离表相比,同期印度天文学家设计的中心差算法相对比较简单,《太阳历数书》等三部印度历法中的月亮中心差算法又表现出不同的传统,《太阳历数书》采用三角函数计算月亮中心差,《宝莉莎历数书》采用分段函数计算月亮中心差,而《罗马伽历数书》将一个近点月等分为24段,直接给出了每一段内月亮实行分与平行分的差值。 2)古代中国和印度月亮中心差算法的起点不同。古代印度历法中,一般以远地点作为月亮中心差算法的起点,而中国6世纪之前的天文学家均以近地点作为起点。不过从唐代开始,部分中国历法中的月离表也以远地点作为起点,如《大衍历》和《神龙历》等历法中的月离表就是以远地点起算的,至于这些历法是否受到来自印度的影响,目前很难给出明显的证据。 3)从月球中心差精度方面考虑,中国和印度所取中心差最大值均偏小。根据表3,《太阳历数书》、《宝莉莎历数书》和《罗马伽历数书》中月亮中心差的最大值分别为4.94°,4.01°和4.93°,《乾象历》、《景初历》和《元嘉历》中月亮中心差的最大值分别为5.29°,5.50°和5.24°。由于月亮轨道偏心率变化较大,当月亮轨道偏心率分别取最大值1/15,平均值0.054 9和最小值1/23时,对应的月亮中心差理论结果的最大值分别为7.66°,6.27°和4.98°。由此可以看出,《太阳历数书》和《乾象历》等六部历法中月亮中心差的振幅均与月亮轨道偏心率取最小值时的理论结果比较接近,就接近的程度而言,3部中国历法略优于3部印度历法。1.3 《罗马伽历数书》中的月亮中心差算法
2 中国隋代之前的月亮中心差算法
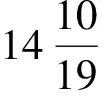
3 中印月亮中心差算法精度分析
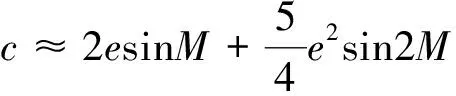
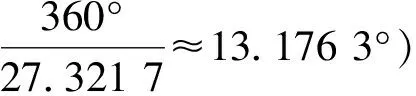
4 结 语

