混凝土箱梁氯离子扩散效应分析与寿命预测的CA模型

(1.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，兰州 730070； 2.兰州交通大学 土木工程学院，兰州 730070)

1 研究背景

与其他建筑材料相比，混凝土具有无定形、制作工艺简便、就地取材、价格低廉等优点，因此在国内外桥梁建设中一直被广泛采用。但当混凝土箱梁长期暴露在含有不同浓度的酸、碱、盐等腐蚀性物质的环境中时，这些腐蚀性的物质会和混凝土的组成成分发生电化学反应，从而使混凝土中钢筋发生腐蚀，最后钢筋锈胀，使混凝土脱落，进一步影响结构的使用性和耐久性[1-2]。目前，国内外很多研究工作者在混凝土结构耐久性方面，尤其是在混凝土氯离子腐蚀性能方面，已经做了大量研究[3-6]。但很少有文献对混凝土箱梁进行研究。在实际桥梁结构中，大量数据显示，每年由于氯离子腐蚀导致桥跨结构提前退出工作的案例不在少数。因此，为了使结构能够达到预期的设计使用年限，本文重点分析和模拟了混凝土箱梁中氯离子传输过程。

氯离子在混凝土中传输机理主要有基于混凝土孔隙的毛细管吸收作用、基于压力梯度的渗透作用和基于浓度梯度的扩散作用。目前，氯离子在混凝土中的扩散过程主要通过Fick第二扩散定律来描述[7-9]，但是由于Fick第二扩散定律的表达式用高斯误差函数来表示，实际的模型分析时往往含有高阶微分方程，而对于高阶微分方程的求解比较繁琐，从而不能被工程设计人员所推广。

为了简化计算，避免高次微分方程的求解，本文基于元胞自动机原理，建立了氯离子在混凝土箱梁中的元胞自动机扩散模型(CA模型)。通过MATLAB编写了计算程序，分析了氯离子在混凝土箱梁中的扩散过程，计算了混凝土箱梁在不同深度、不同时刻、不同位置截面各个部位的氯离子含量，并和解析解作了比较，同时对结构耐久性极限使用寿命进行了预测。

2 元胞自动机原理

元胞自动机(Cellular Automata，简称CA)是把研究对象定义成一个由离散、有限状态的元胞空间，按照一定的局部进化规则，在使用计算机进行计算的基础上，通过与其它相关理论的结合，在离散的时间维度上进化的动力网格系统。元胞自动机主要由元胞、元胞空间、元胞领域、局部进化规则、元胞状态、边界条件和初始条件等构成[10]，其相互关系如图1所示。

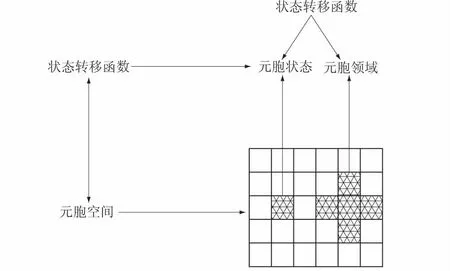
图1 元胞自动机组成示意图Fig.1 Schematic diagram of cellular automata

(1)元胞：元胞是元胞自动机的基本组成单位，是由分布在一维、二维等欧几里德空间网格上的格点构成的。

(2)元胞领域：在运用元胞自动机原理来求解问题之前，必须定义一定的领域规则，确定元胞领域的类型。对于不同类型的元胞空间，应当采用不同维度的领域类型。根据文献[10]和文献[11]，对于二维元胞空间，常采用图2所示的元胞领域。

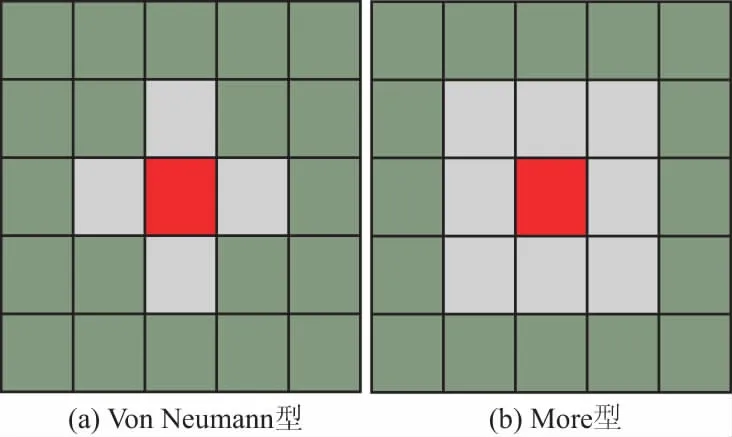
图2 二维元胞领域Fig.2 Cell domain in two dimensions

(3)局部进化规则：是一个状态转移函数，根据中心元胞在某一时刻(t)的状态以及领域元胞的状态来分析下一时刻(t+1)该元胞状态的函数，即

(1)

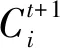
3 基于2D元胞自动机的氯离子扩散模型

3.1 模型的建立

在氯盐等腐蚀性环境下，钢筋混凝土结构随着氯离子扩散作用的进行，钢筋表面氯离子浓度逐渐增加，使得混凝土中的钢筋发生锈蚀。当钢筋表面氯离子浓度值大于某一临界值时，钢筋表面的钝化膜将会发生破坏，从而导致钢筋表面混凝土发生脱落，最终使结构发生破坏，严重影响结构的使用寿命。因此，只要通过研究在使用年限内结构中氯离子浓度的变化，就能够为混凝土结构耐久性设计提供参考依据以及有效地预测结构的耐久性极限使用寿命。

利用元胞自动机的算法来模拟混凝土结构中氯离子的扩散规律，获得结构内任意时刻、任意位置处的氯离子浓度。首先应对研究对象进行网格划分，根据问题的复杂程度，将所要研究的对象在时间和空间上离散成一维或二维的动力网格系统，系统中的每个网格可以看成一个元胞。此时，该元胞的状态就代表了该位置处的氯离子浓度。

本文所建立的氯离子扩散的元胞自动机模型，主要是在采用一定的局部进化规则和元胞领域类型的基础上，通过某一时刻(t)元胞(i，j)以及其领域元胞的状态(浓度)来分析下一时刻(t+1)该元胞的状态(浓度)，从而来获得截面任意时刻、任意位置处氯离子浓度。

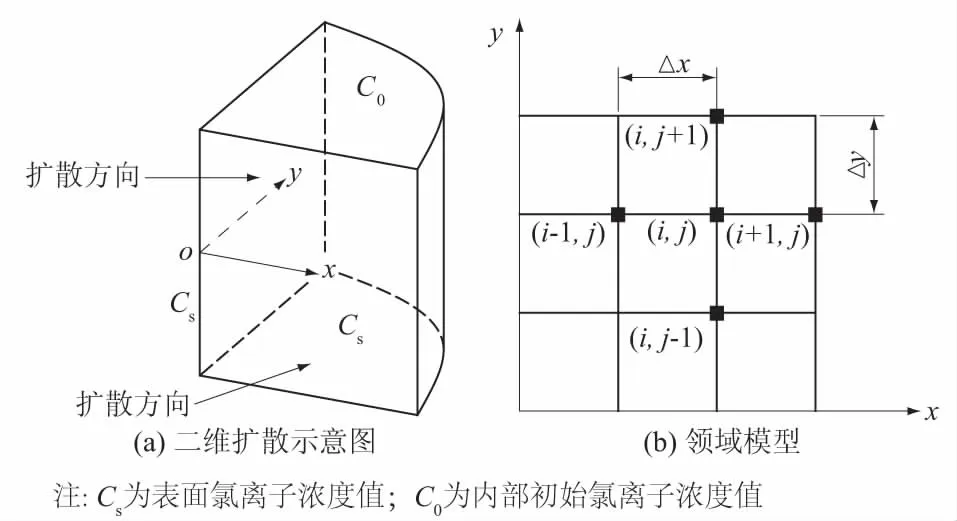
图3 二维1/4无限大体的氯离子扩散与领域模型Fig.3 The diffusion of chloride ion in 1/4 infinitely general and the model of cellular domain

3.2 进化规则的确定

对于元胞自动机模型而言，局部进化规则的制定是必不可少的步骤，氯离子在混凝土中的扩散过程主要通过局部进化规则来实现。对于图3(a)所示的1/4半无限体而言，氯离子在混凝土中的扩散过程属于二维扩散问题。同时，如果将混凝土看成各向同性材料时，二维Von Neumann型的元胞领域将能够很好地解决氯离子在混凝土中的扩散问题。

对于图3(a)所示的1/4半无限体而言，氯离子在混凝土中的二维扩散效应可以进一步地描述为式(2)[12],即

(2)

式中：D为氯离子扩散系数；C为氯离子浓度。

对研究对象划分网格后，取单个中心元胞及领域元胞如图3(b)所示，网格尺寸分别为xi+1, j-xi, j=Δx，yi+1, j-yi, j=Δy，分别在x和y方向上，网格尺寸保持一致。

假定图3(a)所示的二维氯离子在混凝土中的扩散过程满足各向同性，则对于二维氯离子的非稳态扩散微分方程，可以利用中心差分法来求解。差分法是把所求解的基本方程近似地改用差分方程来表示，把求解二维氯离子扩散微分方程的问题转化成求解代数方程的问题。

根据中心差分法[13]，可得：

(3)

(4)

(5)

式中：Δx为元胞沿x方向的尺寸;Δy为元胞沿y方向的尺寸;Δt为氯离子扩散的时间步长。

将式(3)、式(4)、式(5)代入式(2)可得

(6)

假定所有元胞形状大小相等，即Δx=Δy，则上式可进一步简化为：

λ0=1-4DΔt/(Δx)2；

(8)

λ1=DΔt/(Δx)2。

(9)

式中：λ0为位于(i，j)处的中心元胞t时刻氯离子浓度对t+Δt时刻中心元胞氯离子浓度的影响系数；λ1为位于(i，j)处的领域元胞t时刻氯离子浓度对t+Δt时刻中心元胞氯离子浓度的影响系数。

上式即为氯离子在混凝土中扩散的浓度传递公式，即可通过t时刻中心元胞以及领域元胞的氯离子浓度值得到t+Δt时刻该中心元胞的浓度值。通过式(7)、式(8)和式(9)就可建立氯离子在混凝土中扩散的元胞自动机模型。

3.3 模型计算参数的确定

3.3.1 氯离子扩散系数

众所周知，氯离子在混凝土中的扩散过程不是一成不变的，而是一个随时间、材料水灰比等变化的过程。为此，美国混凝土协会进行了大量的试验研究，最终建议混凝土养护28 d时考虑水灰比的扩散系数为

D28=1×10(-12.06+2.4w/b)。

(10)

式中w/b为材料水灰比。

Willam等根据试验研究，发现混凝土中氯离子扩散系数随着时间的推移而逐渐降低。结果表明，扩散系数随时间增长而减小的规律能较好地用幂函数来拟合[1]，即：

Dt=D0(t28/t)m；

(11)

m=2.5w/b-0.6 。

(12)

式中：D0为初始氯离子扩散系数；(t28/t)m为混凝土养护龄期系数；t为结构服役时间；m为扩散系数随时间的依赖指数。

3.3.2 表面氯离子浓度

文献[14]的试验研究发现，混凝土结构表面氯离子浓度往往不是常数，而是一个随时间变化的过程。根据文献中的试验结果，进一步拟合得到混凝土表面氯离子浓度随时间变化的拟合公式，即

Cs=0.196 8t0.104 1，R=0.937 1 。

(13)

3.3.3 临界氯离子浓度

随着氯离子扩散作用的进行，截面内部氯离子浓度逐渐增加，使得混凝土中的钢筋发生锈蚀，钢筋表面混凝土发生锈胀，导致钢筋表面混凝土发生脱落，最终使结构发生破坏。钢筋混凝土结构中，钢筋表面氯离子浓度值大于某一临界值时，钢筋表面的钝化膜将会发生破坏，此时氯离子浓度即为临界氯离子浓度。文献[15]的研究结果表明，对于预应力混凝土结构，临界氯离子浓度一般取为0.13%。

4 模型验证

基于上述理论公式，本文借助MATLAB软件，编写了钢筋混凝土中氯离子扩散的二维CA模型的计算程序。选用文献[16]中的混凝土试件氯离子侵蚀试验，建立氯离子扩散的CA模型，分析计算了混凝土试件中氯离子的扩散过程。试件的尺寸为100 mm×100 mm×100 mm，材料水灰比为0.5。选取立方体试件的中心截面，距离截面端部较远，因此氯离子在其截面内的扩散可以近似地认为是二维扩散。模型中采用的参数分别为：扩散系数D=1.192 7 mm2/d；影响系数λ0和λ1分别为0.5和0.125；模型网格尺寸Δx=1 mm；通过式(9)计算得到元胞进化步长Δt=0.104 8 d。通过MATLAB软件编制的模型计算程序，计算了氯离子在试件横截面内扩散经历30 d和70 d后，距离截面表面不同深度处氯离子的质量分数，结果如图4所示。为了便于比较，图4同时给出了根据Fick第二扩散定律得到的解析解。

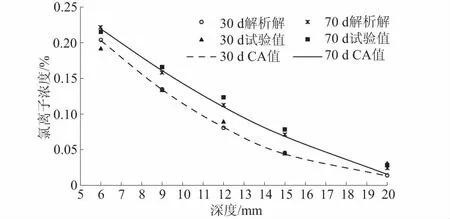
图4 不同时刻混凝土内部氯离子浓度随深度的 变化规律Fig.4 Variation of chloride ion concentration in concrete box girder with depth at different instances

由图4可知，随着扩散作用的进行，氯离子浓度随着深度的增加而逐渐减小。除个别计算点外，元胞自动机模型的模拟结果与采用理论公式计算的解析解非常接近，且与文献中的试验值也非常吻合，说明本文建立的元胞自动机模型能够有效地模拟混凝土中氯离子的扩散过程且精度较高。

5 算例分析

5.1 混凝土氯离子扩散效应分析

本文以我国南部沿海地区氯盐环境下时速为250 km/h的钦防铁路单线箱梁为研究对象。箱梁计算跨度31.5 m，梁宽7.6 m，底板宽3.8 m，跨中截面及配筋尺寸如图5所示，材料水灰比为0.4。列车活荷载纵向采用ZK标准活荷载。梁体采用C50混凝土，弹性模量按规范[14]取值为E=3.55×104MPa，材料泊松比按规范取值为m=0.2。由于桥梁顺桥向尺寸远远大于横桥向尺寸，因此氯离子在混凝土箱梁内的扩散过程可以看成是二维扩散过程，可采用2D元胞自动机模型来分析。选取截面顶板中心、顶板与腹板交接外侧、底板与腹板交接外侧等3个部位的钢筋作为研究对象，如图5所示，分别记为1#钢筋、2#钢筋、3#钢筋。

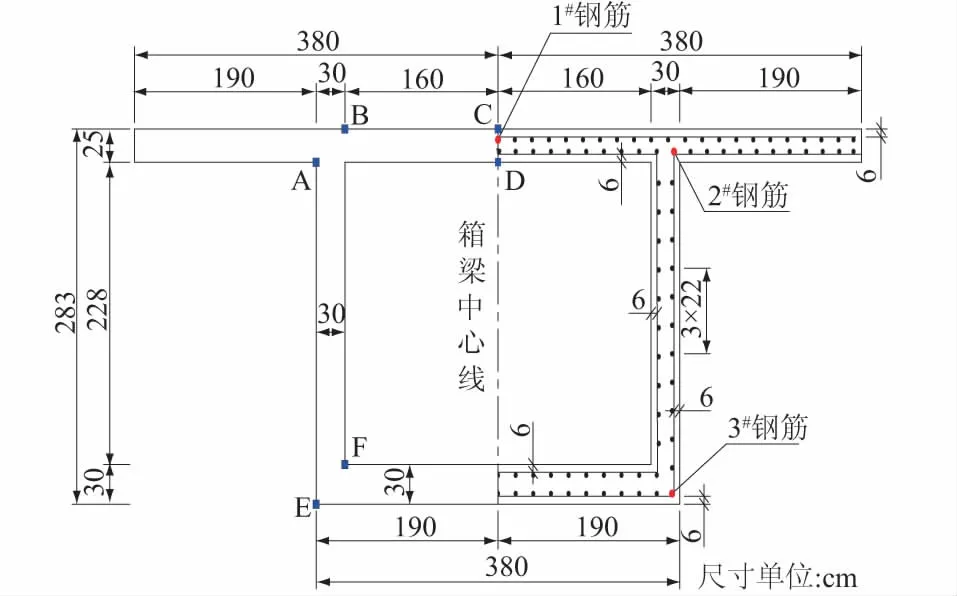
图5 箱梁截面尺寸Fig.5 Dimensions of box girder section

当混凝土氯离子扩散作用进行100 a时，由式(13)计算可得混凝土表面氯离子浓度Cs=0.587 4%。将水灰比0.4代入到式(10)、式(11)和式(12)可得到考虑时间和水灰比后的氯离子扩散系数Dt=0.450 8×10-6mm2/s。选取模型网格尺寸为2 mm，影响系数λ0和λ1分别为0.5和0.125。由式(9)计算得到元胞进化步长Δt=12.838 4 d。为了便于描述，取截面上A点到B点为Ⅰ方向、C点到D点为Ⅱ方向、E点到F点为Ⅲ方向，各个点的位置如图5所示。通过MATLAB软件编制的2D元胞自动机模型计算程序，分别计算了扩散经历50,100 a时截面内各个方向氯离子浓度随深度的变化规律，结果如图6所示。同时，根据程序得到的氯离子扩散过程氯离子浓度分布图如图7所示，该图真实地反映了氯离子在混凝土箱形截面中的扩散过程和变化规律。

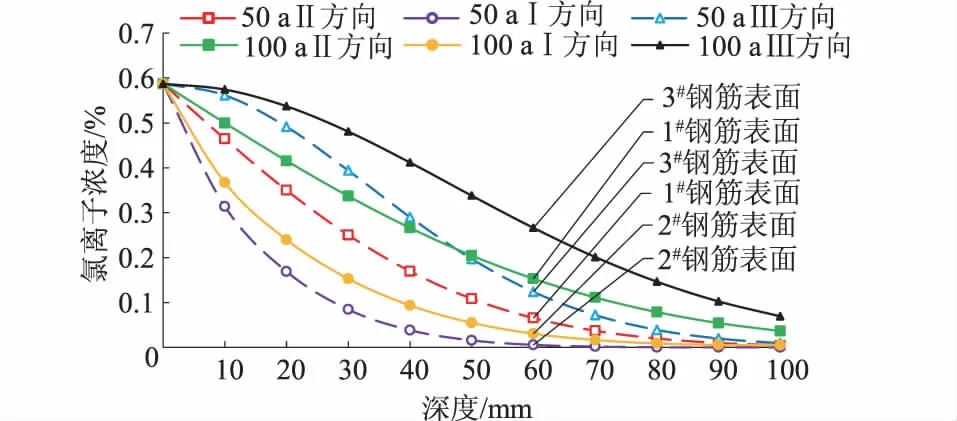
图6 不同时刻各个方向氯离子浓度随深度的变化规律Fig.6 Variations of chloride ion concentration with depth in different directions at different instances

图7 不同时刻截面氯离子浓度分布Fig.7 Distribution of chloride ion concentration in cross section at different instances

从图6可以看出，沿同一扩散方向，随着扩散作用的进行，曲线的斜率逐渐减小，表明氯离子扩散速度随着时间的推移逐渐减小，这是因为随着扩散作用的进行，混凝土内部孔隙逐渐减小以及混凝土内外浓度差逐渐减小的原因造成的。除此之外，随着扩散作用的进行，截面内部氯离子浓度随深度的增加而逐渐减小。

从图6中数值结果来看，2#钢筋保护层位置的氯离子浓度远远小于其他2个位置的氯离子浓度。3#钢筋保护层位置的氯离子浓度明显大于其他同等保护层厚度部位氯离子浓度，主要是因为在这些部位混凝土受到2个方向的扩散作用，因此在结构耐久性设计和结构后期的维修和加固时对此部位应予以重视。对于箱梁这种复杂截面形式的混凝土结构而言，应特别注重截面倒角部位氯离子扩散效应的分析。

从图7可以看出:随着扩散时间的推移，氯离子逐渐从截面表面向截面内扩散，截面同一深度氯离子浓度逐渐增加。根据截面倒角形式的不同，截面内部氯离子扩散呈现出不同的特点，在顶板与腹板相交位置处，氯离子扩散速度小于其他普通位置，是因为氯离子扩散的路径相比其他位置较远造成的；底板与腹板相交位置处，氯离子扩散速度明显大于其他普通位置，主要是由于在此处氯离子受到2个方向扩散作用的影响，这和图6得到的结论相一致。

5.2 结构耐久性使用寿命预测

基于上述建立的混凝土箱梁氯离子扩散的2D元胞自动机模型，本文通过计算得到各个控制点氯离子浓度达到临界氯离子浓度0.13%时的扩散时间，以此来实现结构耐久性使用寿命的预测。根据模型计算程序，计算得到截面各个控制点钢筋表面氯离子浓度随时间的变化规律如图8所示。

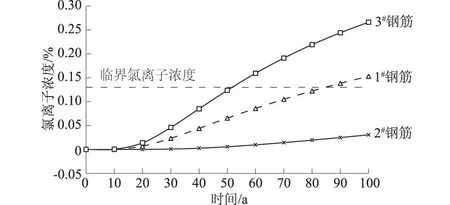
图8 各控制点氯离子浓度随时间的变化规律Fig.8 Variation of chloride ion concentration of control points against time

从图8可以看出:由于截面所处位置的不同，氯离子在混凝土中的扩散呈现出不同的扩散规律。3#钢筋表面氯离子浓度首先达到临界氯离子浓度所需的扩散时间明显少于1#钢筋。主要是由于氯离子在顶板中的扩散主要是从顶板表面沿厚度方向进行的，可认为是一维扩散作用的结果，而底板与腹板相交部位氯离子浓度受到2个方向的扩散作用，是二维扩散作用的结果。而对于2#钢筋而言，即使结构服役100 a，钢筋表面氯离子浓度也不会达到临界浓度。因此，对于该混凝土箱梁而言，3#钢筋表面氯离子浓度达到临界浓度所需的时间即为该结构耐久性服役寿命。

为了直观反映各个钢筋表面氯离子浓度达到临界氯离子浓度所需的最小扩散时间，将图8进一步量化得到表1。表1反映了当各控制点钢筋表面浓度达到临界浓度时所需的最少时间，即为结构的耐久性使用寿命。同时，为了便于比较，表1同时给出了寿命预测的解析解。

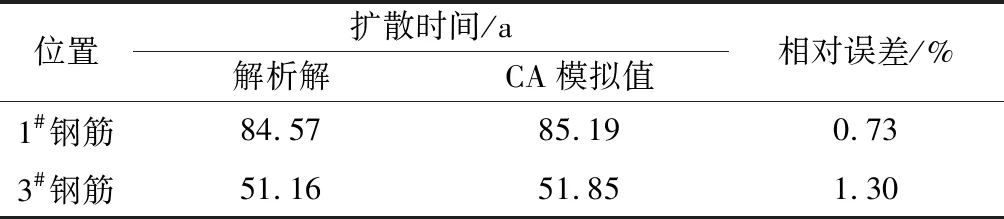
表1 钢筋表面氯离子浓度达到临界浓度所需的扩散时间Table 1 Time required for the concentration of chloride ions reaching the critical concentration on surface of steel bars

由图8和表1可知:该混凝土箱梁桥服役51 a左右,3#钢筋表面氯离子浓度首先达临界氯离子浓度0.13%，因此认为该混凝土结构在服役51 a左右时将达到结构耐久性极限状态。从表1的比较结果来看，本文建立的元胞自动机模型的模拟值和解析解吻合良好，最大误差不超过2%，说明本文方法具有较高的精度，对实际工程具有一定的指导意义。

6 结 论

本文以混凝土箱形截面梁为例，建立了模拟混凝土箱梁中氯离子扩散过程的2D元胞自动机模型，并通过该模型对结构耐久性使用寿命进行了预测，并和解析解进行了对比。通过分析，可以得到以下结论：

(1)与Fick第二扩散定律的解析解相比，本文建立的元胞自动机模型的模拟结果精度较高，可以有效地模拟混凝土箱梁中氯离子侵蚀的过程，可对结构性能退化研究、桥梁结构寿命预测以及耐久性等方面的研究提供一定的参考价值。

(2)随着扩散时间的推移，氯离子逐渐向混凝土截面内部侵蚀。由于箱梁截面倒角形式的不同，氯离子扩散规律呈现出不同的扩散特点，应注重截面倒角部位氯离子扩散效应的分析。

(3)预测结果表明，当该混凝土箱梁服役51 a左右时，箱梁腹板和底板相交位置氯离子浓度最先达到结构耐久性极限设计要求，因此在混凝土结构耐久性寿命设计和对既有混凝土箱梁桥进行后期的维修和加固时对该部位应予以足够的重视。