循环孔隙水压力作用对混凝土动态抗压特性的影响

彭 刚吴 聪乔宗耀马小亮

(1.三峡地区地质灾害与生态环境湖北省协同创新中心，宜昌 443002;2.三峡大学 土木与建筑学院，宜昌 443002)

1 研究背景

国内外学者对处于水环境中混凝土的力学性能开展了大量研究。Wang等[1]研究了粉煤灰掺量、孔隙水饱和度对混凝土回弹值、超声波速、抗压强度和弹性模量的影响；Barani等[2]通过数值模拟证明一个统一的天然裂缝渗透率公式可很好地描述慢速加载和快速加载条件下裂纹扩展的渗透性； Shakiba等[3]的研究结果表明孔隙水压力的作用会加剧沥青混凝土中的损伤，降低其强度；Bai等[4]提出一般的三向应力条件下的孔隙压力增量与主应力增量之间的关系的理论方程；以彭刚为首的课题组[5-9]对混凝土在不同水围压和不同孔隙水压下的动态抗压特性进行了一系列试验，探究在动态加载下，不同的水环境中混凝土峰值应力、应变、弹性模量以及吸能能力的变化规律，并建立相应的损伤模型；王乾峰等[10]研究经历循环荷载后，混凝土在水压力环境中的动态压缩强度。

由上述可知，无论是在理论上还是在试验上，对于混凝土在不同的水环境、不同的受力状态下的研究已经趋于成熟。但在实际工程中，长期处在水环境中的混凝土，很多是在经受多次循环孔隙水压力作用的同时承受着上部的荷载，循环孔隙水压力对混凝土产生的原始损伤会影响混凝土力学参数，在动态加载下会表现出不同的动态特性。为此，对经历20次循环孔隙水压力(0，1，3，5，7 MPa)的饱和混凝土在对应的循环孔隙水压力下进行了常三轴压缩试验，不仅具有理论研究意义，更具有实际工程意义。

2 试验设备及力学试验过程

2.1 试验设备

本次所用试验设备为三峡大学与长春朝阳试验仪器有限公司联合研制的10 MN大型多功能液压伺服静动力三轴仪。该设备可进行常三轴混凝土动静力加载试验，其最大围压值为30 MPa，最大竖向动静力负荷为5 000 kN和10 000 kN。可通过电脑系统控制水压力和轴向加载速率(10-5～10-2s-1)，试验设备见图1。

2.2 试件制作与加工处理

试验所用的水泥为P · O42.5普通硅酸盐水泥；拌合水为饮用自来水；粗骨料是粒径为5～40 mm的连续级配碎石；细骨料是连续级配天然河砂，经过筛分后实测细度模数为2.3，属中砂。混凝土的配合比如表1所示。

图1 试验设备Fig.1 Test equipment

表1 混凝土原材料用量Table 1 Material content of concrete kg/m3

混凝土试件尺寸为Φ300 mm×600 mm，成型方式为钢模浇筑。为搅拌均匀，采取先干拌后湿拌的方法。振捣完成后，将表面抹平处理，室温下放置24 h后拆模，拆模后，将混凝土放入标准养护室养护，保证相对湿度>95%，温度为(20±2)℃，28 d后将混凝土试件移至室外自然养护。

2.3 试验过程

2.3.1 加载前的准备

(1)将尺寸为Φ300 mm×600 mm的圆柱体混凝土放在水箱中，加水进行预饱和处理，此过程可加速后续饱和处理的过程，缩短试验时间。

(2)浸泡7 d后，将其放入围压桶内，通过EDC控制器发送施加水围压命令，进行加压饱和。

(3)加压饱和完成后，分别施加5种不同中心值(0，1，3，5，7 MPa)的循环孔隙水压，循环次数20次。

(4)约24 h后，20次循环完成。

2.3.2 加载过程

(1)保持水围压不变，将围压桶移至加载框架中，使围压桶和上下传力柱对中。

(2)启动EDC，加油压至3 MPa，以位移控制的方式对混凝土预加载20 kN的力。

(3)正式加载：以变形控制方式，在轴向上按照不同的加载速率进行加载，直至得到完整的变形-荷载曲线。

(4)卸载以及后续处理。

3 力学性能分析

3.1 抗压强度

试验得到混凝土在不同应变速率、不同循环孔隙水压力中心值下峰值应力，如表2，不循环的工况是在应变速率10-5s-1下完成的。由表2得峰值应力随不同循环孔隙水压中心值的变化趋势，见图2。

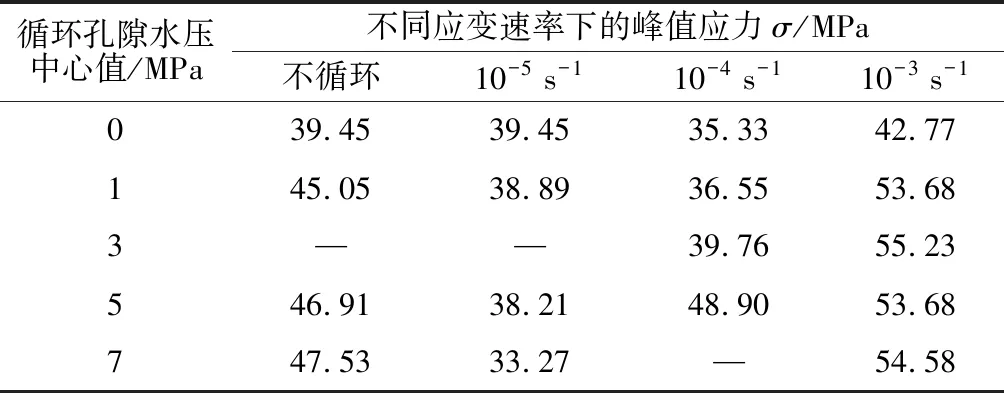
表2 不同工况下混凝土的峰值应力Table 2 Peak stresses of concrete in different working conditions

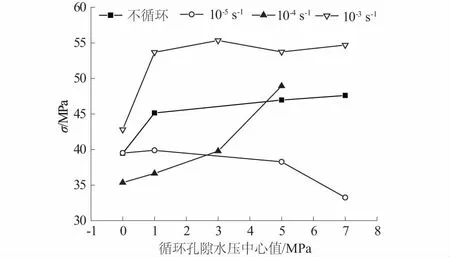
图2 循环孔隙水压中心值与峰值应力的关系Fig.2 Central value of cyclic pore water pressure vs. peak stress

对比分析应变速率为10-5s-1下混凝土的峰值应力，经历不同循环孔隙水压力作预处理后的混凝土较未经历循环孔隙水压的混凝土峰值应力总体有明显降低。经历1，3，5，7 MPa循环孔隙水压力作用后，混凝土强度分别降低13.67%，12.83%，18.55%，30.00%。随着循环孔隙水压力的增大，混凝土强度减少越多，混凝土内部的损伤也增大，说明循环孔隙水压作用对混凝土内部结构产生影响，削弱了混凝土的强度。

随着应变速率的增加，经历不同循环孔隙水压力预处理后的混凝土的峰值应力增大。应变速率为10-4s-1时，在较小的循环孔隙水压力下，混凝土峰值应力有所降低，当循环孔隙水压力继续增大，其峰值应力较未经历循环孔隙水压力的混凝土有明显升高。应变速率为10-3s-1时，不论循环孔隙水压大小，其峰值应力都大于未经历循环孔隙水压以及应变速率为10-4s-1和10-5s-1的经历循环孔隙水压的混凝土的峰值应力。

在10-3s-1和10-4s-1应变速率下，围压较小时，峰值应力增加明显，当围压增加到一定值时，随着围压的增加，峰值应力增加很小。

在循环孔隙水压作用下，有压水会沿着混凝土表层微观裂缝逐步深入到内部，使其内部裂纹数量和分布发生变化，同时使混凝土含水量增加。在动态加载过程中，混凝土内部的含水量对其力学性能影响较大。文献[10]指出，在给定的水压力下，水不能填充全部混凝土孔隙空间，水压力越大，水能渗透到的孔隙直径越小，则对混凝土内部的损伤相对就大。本文试验中，20次循环孔隙水压预处理对混凝土有一个初始损伤，故在10-5s-1应变速率下随循环水压增大，混凝土强度呈减小趋势。而在动态荷载作用下，含水量越高， Stefan效应越明显，混凝土强度越大，故在10-3s-1应变速率下，混凝土的峰值应力最大。混凝土含水量随水压力提高而增加，当水压力超过一定值后，含水量基本不增加，故对混凝土强度影响就比较小，在10-5s-1应变速率下，峰值应力随循环水压的增大，呈现先增大后不变的趋势。

综上分析可知，循环孔隙水压越大，对混凝土内部产生的损伤越大，混凝土强度减少越多。在不同的加载速率下，循环孔隙水压力对混凝土整体强度的影响不同，在准静态和低应变速率下，循环孔隙水压对混凝土强度削弱作用比较明显，表现为混凝土强度减小。在较高的应变速率下，这种削弱作用逐渐减弱，影响混凝土强度的因素主要是应变速率，表现为混凝土整体强度的增加。

3.2 变形特性

不同的加载情况下，经历不同循环孔隙水压后，混凝土的峰值应变如表3，变化关系曲线如图3。

表3 不同工况下混凝土的峰值应变Table 3 Peak strains of concrete in different working conditions

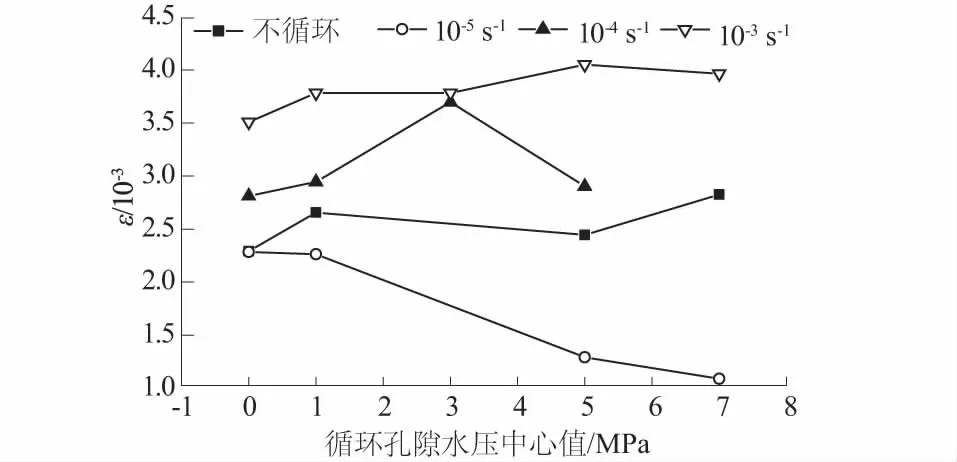
图3 循环孔隙水压中心值与峰值应变的关系Fig.3 Central value of cyclic pore water pressure vs. peak strain

由表3和图3可发现，在应变速率10-4s-1和10-3s-1下，循环孔隙水压力对峰值应变(略有增大)的影响较小，相对10-5s-1应变速率下，其峰值应变都明显增大。

在较低的应变速率(10-5s-1)下，峰值应变随着循环孔隙水压力的增大呈现明显的减小趋势。对比分析应变速率为10-5s-1时，经历循环孔隙水压力作用和不经历循环孔隙水压力作用的情况可以看出，循环孔隙水压力作用使混凝土的峰值应变降低。并且，循环孔隙水压力作用值越大，峰值应变降低越多。

对比表3中的数据发现，经历循环孔隙水压力作用后，混凝土的峰值应变随着应变速率的增大呈增大趋势。这一变化趋势与文献[11]的研究结果相似，但局部趋势有所不同。文献[11]的研究结论为经历循环孔隙水压作用后混凝土的峰值应变随着应变速率的增大先略有减小再增大。可能的原因是：本文试验对混凝土施加循环孔隙水压力时每一次水围压变化后均保持足够的时间，使水围压能够充分向饱和混凝土内部传递从而产生与水围压基本等值的孔隙水压力，而在文献[11]的研究中没有考虑水围压向混凝土内部传递的时间。

3.3 弹性模量

弹性模量反映混凝土的基本力学性能，是表征混凝土力学性能的重要参数之一。当混凝土内部存在有压孔隙水时，循环孔隙水压作用可能会对混凝土的弹性模量产生一定影响[12-13]。本文以混凝土轴心抗压强度35%～55%时应力-应变曲线的割线模量作为混凝土弹性模量的代表值，其数学表达式为

(1)

式中：E表示弹性模量；σ0.55，σ0.35分别为55%，35%对应的峰值应力；ε0.55，ε0.35分别为55%，35%对应的峰值应变。

表4为不同应变速率下的混凝土在不同循环孔隙水压力下的弹性模量值，由表4可得图4。

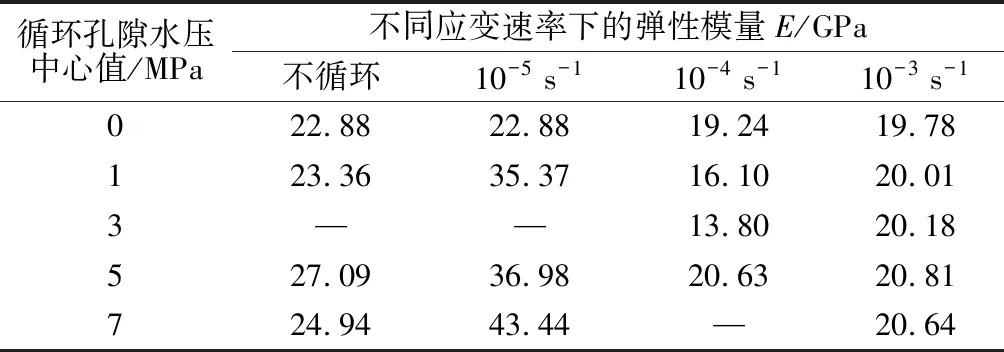
表4 不同工况下的弹性模量Table 4 Elastic modulus in different working conditions

图4 循环孔隙水压中心值与弹性模量之间的关系Fig.4 Central value of cyclic pore water pressure vs. elastic modulus

由表4和图4可知，当应变速率为10-5s-1时，混凝土的弹性模量随着加载时孔隙水压力的增加呈增大趋势。在较高应变速率下(10-4s-1和10-3s-1)，随着循环孔隙水压力值的增大，弹性模量的变化不大。对比分析应变速率为10-5s-1时，经历循环孔隙水压力作用与不经历循环孔隙水压力作用的情况，经历循环孔隙作用后的混凝土弹性模量有所提高，并且预处理过程中循环孔隙水压力值越大提高幅度越大。说明当应变速率较低时，循环孔隙水压力作用对混凝土的弹性模量有提高作用，当应变速率较高时为削弱作用。

4 应力-应变全曲线拟合分析

4.1 Weibull-Lognormal模型

根据文献[14]、文献[15]的研究，采用Weibull-Lognormal模型能够较好地拟合混凝土应力-应变曲线。该模型中，在应力上升阶段采用Weibull分布，在应力下降阶段采用Lognormal分布。选取该模型对得到的应力-应变曲线数据进行拟合计算，其应力-应变本构关系表达为

(2)

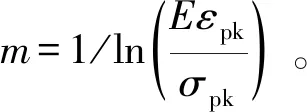
4.2 规范推荐的本构模型

另外，本文采用《混凝土结构设计规范》(GB 50010—2010)推荐的应力-应变曲线模型对试验所得数据进行拟合。规范中混凝土的应力-应变曲线表达式为

(3)

(4)

(5)

(6)

式中：σ为应力；ε为应变；Ec为弹性模量；εc,r为单轴抗压强度相对应的混凝土峰值应变；fc,r为单轴抗压强度代表值；αc为形状控制参数；x为应变发展水平；n,ρc为常数。

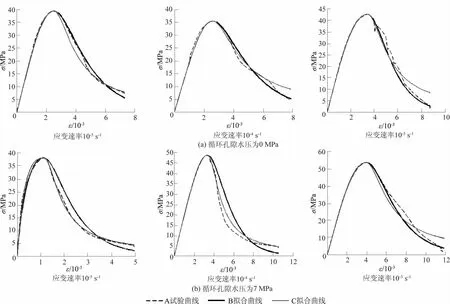
图5 不同循环孔隙水压及不同应变速率下的应力-应变曲线拟合结果Fig.5 Fitted stress strain curves under varying cyclic pore water pressure at different loading rates

通过以上2个混凝土的本构模型来对加载得到的试验数据进行拟合，并与试验所得数据对比分析。

图5为混凝土经历不同循环孔隙水压力作用后，以不同的应变速率在相应的有压孔隙水环境下加载得到的应力-应变曲线及2种拟合曲线。图5中A试验曲线为加载得到的混凝土应力-应变曲线；B拟合曲线为使用Weibull-Lognormal模型进行拟合得到的对应工况下的混凝土应力-应变曲线；C拟合曲线为使用规范推荐的本构模型拟合得到的混凝土应力-应变曲线。通过MatLab内置的Corrcoef函数来求得2种模型的相关系数，根据相关系数值的大小来对比分析2种模型的拟合效果。

由图5可以看出，2种模型都能对本文设定工况下加载得到的应力-应变曲线很好地拟合，在以上工况下的相关系数的均值都在0.97以上。尤其在应力-应变曲线的应力上升阶段，通过2种模型拟合的曲线基本与试验曲线重合，2种模型对应力上升阶段曲线的拟合取得了很好的效果。在应力-应变曲线的应力下降阶段，2种模型都拟合出了曲线的基本形状，满足拟合要求。但是对比可以发现，Weibull-Lognormal模型对应力下降阶段的拟合效果较为优异。使用Weibull-Lognormal模型对应力-应变曲线下降段拟合的相关系数约为0.974，而使用规范推荐模型对应力-应变曲线下降段拟合的相关系数约为0.941，说明Weibull-Lognormal模型对曲线下降段的拟合更为接近试验真实情况。

5 结 论

(1)循环孔隙水压作用会对混凝土内部产生损伤，相对于没有经历循环孔隙水压的准静态加载下的混凝土，其强度会降低。在高应变速率下，影响混凝土强度的主要因素是加载速率，而循环孔隙水压力对混凝土强度的削弱作用减小。

(2)经历循环孔隙水压后的混凝土的峰值应变和弹性模量在高、低应变速率下表现出不同的性质。在低应变速率下，混凝土的峰值应变和弹性模量随循环孔隙水压的增大而总体升高，在高应变速率下，随循环孔隙水压的增大总体变化小。

(3)采用的Weibull-Lognormal模型和规范推荐的模型对应力-应变曲线的拟合效果都比较好。相比较而言，在曲线的下降段，Weibull-Lognormal模型的拟合效果比规范推荐的模型拟合效果好。