基于界面本构模型的锚杆张拉受力分析

刘 波1，胡卸文1，白凯文，陈浩栋，郑智洋

(1.西南交通大学 地球科学与环境工程学院， 成都 611756; 2.西南石油大学 地球科学与技术学院， 成都 610500)

1 研究背景

注浆锚杆或锚索大量地应用于隧道支护、岩石边坡锚固以及其他岩土工程中。锚杆荷载-位移关系的预测、侧阻力的分布模式、荷载传递以及锚固体与土体、岩体或混凝土界面的剪切变形特性，一直是工程中关注的焦点。

为预测锚杆拉拔时的荷载-位移曲线，研究者大多从2种思路出发:一种是建立合适的数学模型拟合锚杆现场抗拔荷载-位移关系曲线，从而确定锚杆的极限荷载标准值，如双曲线函数模型[1]、指数函数模型[2]、SVM回归模型[3]、Weibull数学模型[4]以及改进指-幂混合函数模型[5]；另一种思路则是基于确定锚固界面的本构模型及其参数，利用荷载传递微分方程求解荷载-位移曲线[6-7]，同时求解出不同拉拔荷载下，锚杆界面剪应力的分布情况，这种思路从机理出发，理论上相对严谨。

在锚杆界面剪切滑移本构模型的建立上，众多的研究学者提出了线性增长型[8-9]、双折线硬化型[6]、双曲线硬化型[10-11]、理想弹塑性型[7,12]、一次跌落型[13-17]、三折线软化型[18-22]以及四折线软化型[23]，并分别对锚杆锚固体的受力变形特性进行了理论分析。上述模型中，虽然有些模型能给出锚杆受力分布的解析表达，而实际锚杆界面的剪切滑移为连续曲线的形态，上述模型部分采用分段描述的方式，具有一定的误差；部分为硬化型模型，不能刻画多数情况下界面的软化特征；且参数确定依赖室内试验以及工程经验。

黄明华等[24]通过实际工程中锚杆现场拉拔试验，从荷载-位移曲线出发建立锚固界面的双指数曲线本构模型，并用于锚杆受力分析。但由于假设荷载-位移曲线采用指数形式，且其建立的本构模型不能反映残余强度，因此存在一定的局限性。但其逆向求解的思路具有借鉴价值。

本文引入2种反映残余强度的锚固界面剪切滑移模型：统计损伤模型以及改进Duncan-Chang模型。借鉴上述思路，根据锚杆张拉过程中的荷载-位移实测数据，采用粒子群优化算法反演模型参数，并应用到锚杆受力的正分析中，从而实现锚杆荷载-位移关系以及侧阻力分布的预测，以期为锚杆的设计和施工产生积极的反馈作用。

2 2种锚固界面软化本构模型

为较为准确地描述具有软化特征的锚杆界面剪切滑移本构关系，至少需要2个特征点的坐标：峰值点以及刚达到残余强度的特征点，因此本构模型里至少需要包括4个参数。本文引入2种考虑残余强度的连续曲线形式的锚杆界面本构模型，作为下文分析的基础。

2.1 锚固界面统计损伤本构模型 (S-D模型)

笔者曾根据统计损伤理论[25]推导并建立考虑残余剪切强度的锚固界面本构模型，具体形式为

(1)

式中：τ为锚杆界面微元某一时刻剪力；K为锚杆界面未损伤时单位剪切位移对应的剪切应力；u为锚杆界面宏观剪切位移；u0为锚杆剪切面的宏观平均极限剪切位移；m为反映剪切面强度分布均匀性的参数；τr为锚杆界面的残余剪切强度。则有

(2)

当u=0时，dτ/du=K，即剪切滑移曲线的初始切线斜率=K；当u→,τ→τr，即τr表征了界面的残余剪切强度。

当K=0时，式(2)退化为

(3)

式(3)为硬化型的三参数曲线模型，而指数曲线模型也是当m=1时的特例。u0和m为界面微元强度服从Weibull分布时的分布参数，影响模型曲线的分布形态。

2.2 改进 Duncan-Chang 模型 (ID-C模型)

为描述砂岩破坏过程的应力-应变响应，王军保等[26]提出了改进Duncan-Chang模型，以弥补Duncan-Chang 模型在反映岩石应变软化特性方面的不足。本文引入该软化模型，并对其形式稍作修改，以刻画锚杆界面的软化特性，具体表达形式为

(4)

式中a,b,m,n为锚固界面参数。

当u→时,τ→b，即b是反映锚固界面残余剪切强度的特征参数。

将τ对u求导可得

(5)

当u=0时，dτ/du=a/n，即a/n为剪切滑移曲线的原点处切线斜率，初始剪切劲度系数K0=a/n。而参数m和n为影响曲线分布形态的参数。

3 锚固体锚固荷载传递模型

为分析锚杆的荷载传递特性，选取锚固微段dx作为研究对象，如图1所示。P(x)为锚固体界面轴力；τ(u)为锚固体界面剪应力。由于微段足够小，可以认为微段上的剪应力均匀分布，并与锚固体与周围岩土体接触面上的相对滑移u有关。

图1 锚固微段受力分析Fig.1 Stress analysis of anchorage segment

建立锚固体单元沿轴向方向力的平衡方程为

dP(x)+Cτ(u)dx=0 。

(6)

式中C为锚固体的截面周长。

由式(6)可以得到

(7)

并满足:

(8)

P(x)=EAεx。

(9)

式中：εx为锚固体界面拉伸应变;E,A分别为锚固体的弹性模量和截面面积。

假设锚固体工作时处在半无限空间体内，即周围岩土体对锚固体的约束作用相同，锚固体界面各锚固深度处均满足相同的剪切滑移本构关系，联立式(7)—式(9)，可得

(10)

式中d为锚固体直径。

式(10)满足初值条件：

(11)

式中：l为锚固深度;s为锚固体顶端张拉位移。

由于τ(u)往往形式复杂，式(10)为二阶非线性微分方程，并无解析解，因此在MatLab中可利用Runge-Kutta法迭代求解可得到满足实际工程精度要求的关于u=u(x)的数值解。

锚固体在锚固深度x上各点的轴力以及界面剪切摩阻力可根据式(13)和式(14)求解，即：

(13)

τ(x)=τ[u(x)] 。

(14)

4 基于粒子群算法的接触面模型参数反演

4.1 粒子群寻优算法

粒子群优化算法是基于群体的演化算法，将每个个体看作在D维搜索空间中一个没有质量和体积的粒子，并在搜索空间中以一定的速度飞行[27]。

对于D维的搜索空间,由m个粒子组成的粒子群第i个粒子的当前位置表示为Xi(xi1,xi2,…,xiD),速度表示为Vi(vi1，vi2，…,viD),Pi(pi1，pi2，…,piD)为第i个粒子的历史最优位置，Pg(pg1，pg2，…,pgD)为该粒子群的历史最优位置。

对初始粒子位置和粒子速度赋予随机值，在每次迭代中，每个粒子根据式(15)和式(16)来更新其速度和位置，即：

d=1,2,…,D;

(15)

(16)

式中：t为当前迭代次数；w为惯性因子；d为方向分量编号；c1和c2为学习因子;r1和r2为[0，1]间均匀分布的随机数。

粒子群算法的基本思想是每个粒子充分利用群体和自身的智能，不断地调整学习，最终得到最优解。

4.2 锚杆荷载位移曲线与界面本构模型关系

锚杆界面剪切滑移的模型关系可以表示为

τ=τ(u) 。

(17)

将式(17)代入式(10)和式(13)，并根据式(11)和式(12)给出的初值条件求解，即可以得到u(x)和P(x)的表达式。并可得到锚杆顶部张拉位移S=u(x=0)，锚杆顶部荷载P=P(x=0)。这样就建立了锚杆荷载位移曲线与界面剪切滑移本构模型间的关联。

4.3 接触面模型参数反演过程

根据4.2节内容，可知当界面本构模型中的4个参数确定，且锚杆顶部位移确定时(初值条件)，根据荷载传递模型解答可以得到锚杆顶部荷载P的数值。因此，接触面模型参数的反演过程就是，根据锚杆顶端张拉数据，即P-S曲线，求解界面模型中4个参数的过程。

构建目标函数为

(18)

其中，

X=(k,u0,m,τr) 或X=(a,b,m,n)。

式中:X为一组待反演参数, 其中k,u0,m,τr为S-D模型参数，a,b,m,n为ID-C模型参数；Pi(X)为第i个锚杆顶部位移对应的锚杆荷载计算值；Pi为第i个锚杆顶部位移对应的锚杆荷载实测值；n为选取实测拉拔曲线上关键位移荷载点的个数。

利用粒子群优化算法编程简单、全局搜索能力强、收敛速度快的优势，进行优化求解，反复迭代，寻找到合适的锚杆界面模型参数，使求解得到的不同张拉位移下的锚杆顶部荷载与实测值最为接近，即目标函数最小。

5 算例分析

为验证本文引入的锚杆界面本构模型的可靠性，以及接触面模型参数反演思路的合理性，本文选用荣冠等[28]以及刘波等[29]完成的锚杆张拉过程的试验数据加以反演，在求解得到模型参数的基础上，对锚杆张拉试验曲线以及张拉过程中锚杆轴力、剪应力分布进行计算，并用试验结果检验模型的合理性。

5.1 钢锚杆室内张拉试验数据反演与分析

为了解砂浆锚杆工作机制，合理进行锚固工程设计计算，荣冠等[28]设计了螺纹钢锚杆和圆钢锚杆拉拔试验，锚杆直径为32 mm，弹性模量为210 GPa，设计锚固长度为1 m，锚杆直接浇埋在混凝土中。并在锚杆上布置电阻应变片以测量不同锚固深度处锚杆的应力值。

2种锚杆界面剪切滑移模型的参数见表1,锚杆张拉试验数据及反演结果如图2所示。

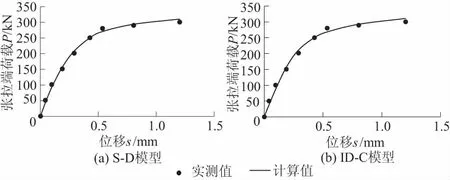
图2 室内试验锚杆荷载-位移曲线计算值与实测值Fig.2 Calculated and test values of load-displacement curve of anchor

S-D模型参数ID-C模型参数ku0mτrabmn63.310.2241.2240.446154.160.240.1673.16

分别以2种模型的反演参数进行正分析，利用锚杆荷载传递微分方程，求解不同张拉荷载下，锚杆锚固深度各点轴力以及剪应力分布，见图3和图4。

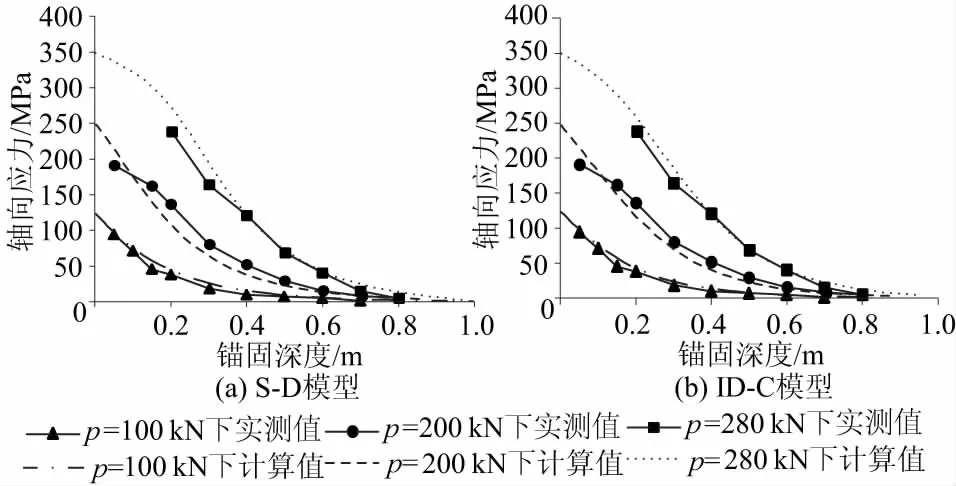
图3 室内试验锚杆各处轴力计算值与实测值Fig.3 Calculated and indoor test values of bolt’s axial force

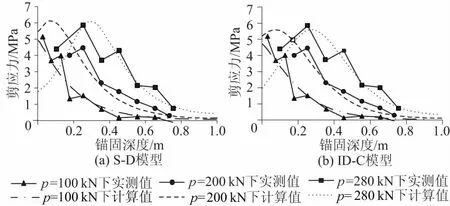
图4 室内试验锚杆界面剪应力计算值与实测值Fig.4 Calculated and indoor test values of interfacial shear stress of anchor

从图3和图4可以看出，锚杆轴力及界面剪应力的试验数据与根据反演参数计算的结果十分吻合，证明了上述方法的可行性。

从图4可以看出拉拔过程中锚杆受力的变化情况：随着锚杆顶部拉拔荷载的增加，锚杆接触面的剪切摩阻力经历了增长、达到峰值并软化的过程，当张拉荷载相对较小即锚固界面处于弹性黏结状态时，剪应力的最大值在张拉端，并大致按幂函数或双曲函数分布，这与许多关于锚杆传力机理的弹性理论研究结果相一致[8,30]；随着张拉荷载的增大，锚杆张拉端剪应力超过锚固界面的极限剪切强度，剪应力最大值逐渐移向远端，以渐近方式发生滑移并改变剪应力的分布形式，呈现单峰曲线的形态。

从图4也可以看出，当上拔荷载达到>200 kN的某一个数值时，随着荷载的增加，锚杆顶部区域的剪切应力出现峰后衰减。由于锚杆轴力增量与界面剪切应力具有平衡关系，即dP(x)+Cτ(u)dx=0，τ(u)减小，在剪切应力的峰后区域，锚杆轴力也同步出现了软化，如图3所示，同时随着拉拔荷载增加，软化深度由锚杆顶端区域向远端扩散。

5.2 某山区岩石基础现场拉拔反演与分析

刘波等[29]在一山区进行岩石基础锚固拉拔现场试验，锚固钢筋直径为42 mm，钢筋的弹性模量为2.0×105MPa，锚固长度为3 000 mm。钢筋周围灌浆采用单轴抗压强度27.10 MPa的细石混凝土，变形模量为2.6×104MPa，钻孔直径为150 mm。在钢筋上开槽，并间隔150 mm布设应变片。在上拔过程中记录锚杆顶部位移和锚杆轴力的变化。采用同上的方法，反演得到的模型参数见表2，反演分析得到的锚杆拉拔曲线与不同张拉荷载下锚固体轴力分布如图5和图6所示。

表2 模型反演参数Table 2 Inversion parameters of model

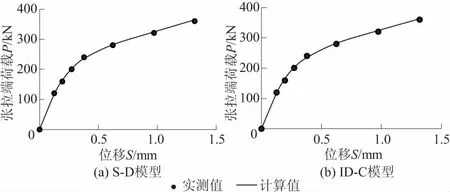
图5 现场试验锚杆荷载-位移曲线计算值与实测值Fig.5 Calculated and field test values of load-displacement curve of anchor

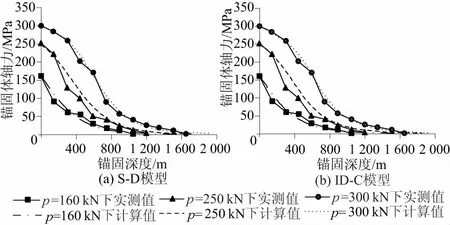
图6 现场试验锚杆各处轴力计算值与实测值Fig.6 Calculated and field test values of bolt’s axial force

从图5和图6可以看出，不同张拉位移对应的锚杆顶部荷载计算值与实测数据误差很小，锚杆轴力反演参数计算结果与试验数据也十分吻合，再次证明了本文反演再分析方法的合理性。

并根据上述过程得到的反演参数，绘制本文中5.1节案例1和5.2节案例2的2种锚杆界面剪切滑移模型的本构关系曲线，如图7所示。

图7 锚杆界面剪切滑移本构模型曲线Fig.7 Shear-slip constitutive models of anchor interface

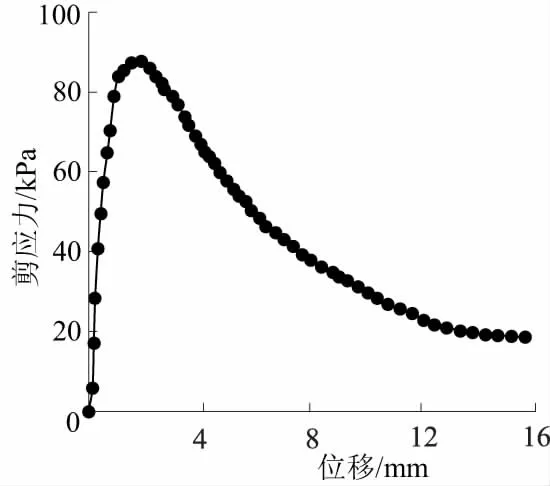
图8 锚杆界面剪切滑移曲线Fig.8 Shear-slip curve of anchor interface

陈昌富等[31]为真实反映锚杆受拉时锚固体与岩土体界面的特性，较准确地获得包含界面剪切残余段的剪应力-位移全过程曲线，研发了一种锚-土界面摩阻性能测试仪器，获得的锚-土界面剪应力-滑移曲线如图8所示。同图7相比，文献[31]的试验曲线与本文反演求解的模型曲线都具有初始弹性、非弹性、峰值后软化以及残余剪切强度阶段，在形态上具有很高的相似性，再一次验证了本文引入的2种锚杆界面本构模型的合理性。

6 结 论

(1)本文引入2种反映残余强度的锚固界面剪切滑移模型(统计损伤模型以及改进Duncan-Chang模型)，并分析了2种模型各参数的物理意义。提出根据荷载-位移曲线，采用粒子群优化算法反演模型参数，再应用到锚杆张拉受力的正分析中，从而实现了锚杆荷载-位移关系以及侧阻力分布的预测方法。

(2)通过实例分析，上述方法计算得到的锚杆荷载-位移曲线、锚杆轴力以及界面剪应力分布与实测值较为接近，证明了本文引入的锚杆界面剪切滑移模型的合理性，模型参数反演方法的可操作性，以及由现场拉拔试验数据参数反演、再应用到锚杆受力分析这种思路的可行性。

(3)随着拉拔荷载的增加，锚杆顶部的剪切应力增长至峰值点后衰减，剪切应力分布曲线进一步向锚固深度内传递，锚杆轴力也同步经历软化的过程。锚杆张拉是荷载逐渐传递的过程。

本文提出的根据锚杆张拉试验数据参数反演再应用到界面受力正分析的方法，具有求解精度高、可操作性强的优势，可以为锚杆的设计和施工提供一定的参考。