井下圆球运动分析与新型试压体设计

王乐顶，王怀婧，陈新海，槐巧双，李晓勇

(1.中国石油集团渤海钻探工程有限公司井下技术服务分公司，天津 300283；2.中国石油集团渤海钻探工程有限公司工程技术研究院，天津 300283；3.中国石油集团渤海钻探工程有限公司工程技术研究院，河北 任丘 062552)

0 引言

在油、气、水井井下作业中涉及圆球的应用较多，如试油(气)作业中管柱的投球试压与反洗球、压裂作业中的投球坐封和打开滑套以及分段(层)压裂时的堵塞球等。然而在现场施工中存在以下两个问题：(1)圆球何时到达设计点？现场试压、坐封、打开滑套圆球入座和压裂堵塞球到达目的层位时的时间主要凭借经验来判断，缺少理论依据。(2)管柱试压反洗球耗时长。在一些无法使用可砸泄试压工具的管柱试压中，利用投球试压、反洗球较多，然而在反洗球施工时耗时往往较长。以施工井Z1井(直井，井深3650 m)为例，在2台700型水泥泵车排量800 L/min的条件下，洗球耗时150 min，在消耗成本的同时也将施工周期拖长。

因此，针对以上问题，有必要对圆球在管内的运动规律进行分析，以期解决圆球到达设计点时间(即候球时间)的准确预判和提高反洗球时效的问题，从而提高井下作业时效降低施工成本。

1 国内外研究进展

国内，2007年西南石油大学的杨文领等[1]提出筛管悬挂器投球下落速度计算方法并通过实例进行验证，确定使用牛顿-雷廷格公式计算最为准确；2011年西南石油大学的肖晖等[2]教授对投球压裂堵塞球运动方程进行研究，分析了堵塞球密度、施工排量和液体粘度等参数对堵塞球运动状态，特别是堵塞球最终运动速度(即沉降末速)的影响。2016年川庆钻探的温杰文等[3]通过对直井段和斜井段自由沉降的钢球进行受力分析建立速度计算模型，得出投球式封隔器实践应用中候球时间的量化计算方法。该方法通过简化将圆球的沉降末速作为平均速度来计算，忽略了圆球加速运动阶段。

国外，2004年希腊克里特理工大学的Kelessidis[4]教授通过现场数据研究了圆球在牛顿和非牛顿流体时的沉降末速并分析了其影响因素。2012年伊朗沙尔鲁德理工大学的Rooki等[5]利用人工神经网络来预测圆球在牛顿流体和幂律流体下的沉降末速。2017年丹麦技术大学的Vertchenko[6]研究了在低雷诺数下利用斯托克法计算不同直径圆球的沉降速度并进行分析。

通过以上文献调研分析，沉降末速作为研究圆球运动规律的重要参数，针对圆球沉降末速的计算主要有以下方法。

(1)斯托克(Stokes)计算法：

(1)

式中：vt——圆球沉降末速度，m/s；g——重力加速度，9.81 m/s2；db——圆球直径，m；ρb——圆球密度，g/cm3；ρf——压井液密度，g/cm3；η——压井液粘度，mPa·s。

式(1)的使用条件是球形颗粒在牛顿流体中沉降，且颗粒的雷诺数Re<1，即慢速沉降。

(2)牛顿-雷廷格计算法：

(2)

式(2)适用范围为雷诺数Re在103～105之间。

(3)水力学计算法：

(3)

式(3)适用的范围：当雷诺数Re<1时，绕流阻力系数CD=24/Re，此时符合斯托克定律，即为斯托克计算法；当雷诺数Re在103～105之间时圆球绕流阻力系数CD可取0.44～0.50，具体可通过查附录图和公式确定。通过观察可知，当绕流阻力系数CD取0.50时，即为牛顿-雷廷格计算法。因此，斯托克计算法和牛顿-雷廷格计算法为水力学计算法的特殊情况。

2 圆球运动分析及候球时间计算

圆球在管内的运动状态一般分为3种情况：圆球自由沉降入座；泵送圆球沉降入座；反洗试压球，如图1所示。

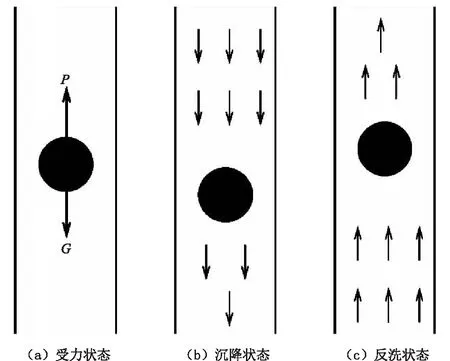
图1 圆球受力分析及不同工况的运动状态Fig.1 Force analysis of the ball and its movement under different working conditions

通过借鉴国内外文献[7-16]中对圆球的研究，对圆球在井下的运动规律进行分析，同时，将研究结论与现场应用相结合，来对施工作业做出优化。根据文献[9]，在两相流动中，Basset力是由于相对速度随时间的变化而导致颗粒表面附面层发展滞后所产生的非恒定气动力。对于尺寸较大的颗粒，忽略Basset力不会造成较大的计算误差，因此对圆球受力分析时选择忽略Basset力。

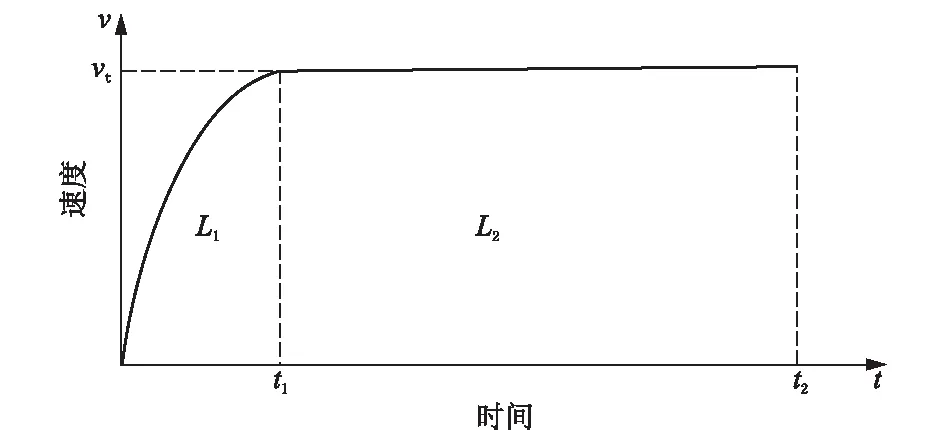
图2 不同时间下圆球速度的变化规律Fig.2 Ball velocity changes at different times

根据受力分析可知，圆球在井下的运动分为两个阶段：一是加速运动阶段L1，随着圆球速度的增加，阻力越来越大，加速度越来越小；二是匀速运动阶段L2，当速度增加到一定程度，阻力、浮力与重力平衡时，加速度为0，圆球以匀速运动，此时的速度即为沉降末速度vt。

重力：G=mg=1/6πdb3ρbg；浮力：P=1/6πdb3ρfg；阻力：D=1/8πCDρfdb2vt2。

因为：

则有：

又根据运动过程边界条件：

圆球到达设计点时间为：

(4)

式中：H——投球到达设计点的垂深，m；vt——试压球沉降末速度，m/s；g——重力加速度，9.81 m/s2；db——圆球直径，m；ρb——圆球密度，g/cm3；ρf——压井液密度，g/cm3；η——压井液粘度，mPa·s；CD——绕流阻力系数，无因次。

通过对新的候球时间计算公式分析可知：圆球候球时间主要与设计点的垂深H和圆球沉降末速度vt有关。对沉降末速度的计算公式即式(3)进行分析得：影响沉降末速的主要因素为绕流阻力系数CD、圆球直径db、圆球密度ρb和压井液性能(密度和粘度)。在以上影响因素中，绕流阻力系数在已知三维物体的形状与尺寸条件下主要取决于温度及在该温度下流体的密度、粘度与运动状态。压井液性能是相对而言容易调整的。可以通过改变三维物体的形状与尺寸来降低绕流阻力，从而缩短“候球时间”和反洗施工时间，优化施工设计和提高施工效率。

3 新型管柱试压体设计构思

根据空气动力学定义将物体形状分为流线型和非流线型两种。流线型即不出现边界层分离的形状，相对于流线型，圆球则属于非流线型中的钝体。物体形状不同其绕流阻力系数差异也很大，具体见表1。

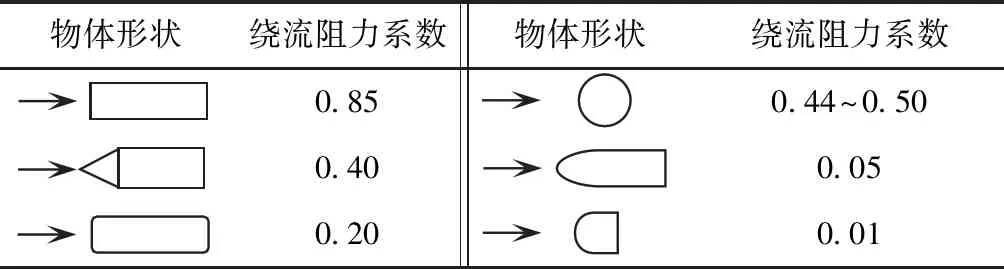
表1 常见三维物体绕流阻力系数CD对比(Re>104)Table 1 Comparison of drag coefficient CD of common 3D objects(Re>104)

通过借鉴列车、船舶及水下航行体的流线型设计并参考仿生鲹科鱼类游动力学研究[17-20]。在几种常用流线型体(卡克斯流线型、双半椭圆流线型、半椭圆+抛物线流线型和半椭圆+圆弧流线型)轮廓方程的基础上，得出半椭圆+圆弧流线型的阻力系数最小[20]。该流线型的进流段是半椭圆，去流段是一段圆弧，具体曲线方程为：

(5)

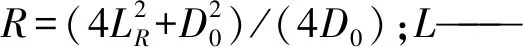
鉴于以上曲线方程并结合工程实际设计出一种新型管柱试压体，如图3所示。流线体具体参数为：最大横剖面直径60 mm，进流段长度40 mm，去流段长度120 mm，圆弧半径255 mm。

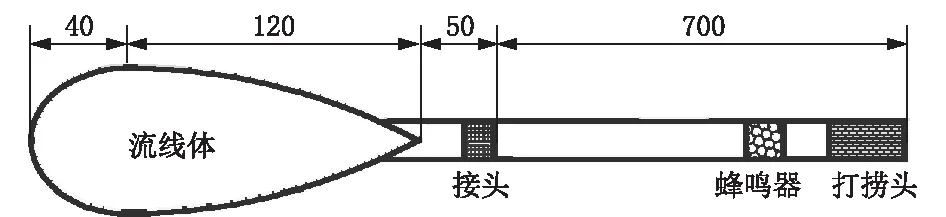
图3 新型管柱试压体示意图(以Ø73 mm N80平式油管为例)Fig.3 Schematic diagram of the new pressure test body

新型管柱试压体由流线体和打捞杆两部分组成。(1)流线体由流线减阻头和接头构成，减阻头属于半椭圆+圆弧流线型构造，通过减阻头能有效降低试压体入座和反洗时的绕流阻力，加快试压体入座和减小反洗难度，提高作业时效；接头的配备便于与打捞杆快速连接。(2)打捞杆的作用主要是在反洗时方便作业人员打捞试压体，而且利用声音在液体中传播较空气中快的原理，在打捞杆中部配备蜂鸣器，在使用试压体时打开电源开关使蜂鸣器处于工作状态。通过在井口监测声音的强弱来判断反洗时试压体的大致位置，便于施工人员打捞，新型管柱试压体的设计构思为进一步优化施工作业奠定了基础。

4 结论

(1)通过对圆球的运动阶段和受力分析得出新的候球时间计算公式，为优化施工设计提供了依据；

(2)圆球绕流阻力系数、圆球直径、圆球密度和压井液性能(密度和粘度)是影响候球时间的关键因素；

(3)设计提出了一种新型管柱试压体设计构思，与圆球试压体相比，该试压体应具有更小的绕流阻力；

(4)新的候球时间计算公式和新型管柱试压体设计构思，应通过现场应用进一步完善和改进。