基于FLAC3D对大连某工程桩基承载力数值模拟研究

张 颖，陈 晨，王彧佼，靳成才，张 晗，潘栋彬

(1.吉林大学建设工程学院，吉林 长春 130026；2.自然资源部复杂条件钻采技术重点实验室，吉林 长春 130026；3.中国建筑东北设计研究院有限公司，辽宁 大连 116021)

0 引言

由于大直径钻孔灌注桩具有单桩承载力高、对周边环境影响小，可以在钻孔过程中查实地层情况，根据地层构造选用适当直径等优点，被广泛使用[1-5]。保障建筑物的安全稳定是保证施工人员及住户安全的重要措施。根据资料显示，近几年地基失稳现象层出不穷，其原因是桩基础属于地下工程，周围环境十分复杂，其施工质量检测十分困难，而且易产生误差，同时后期的监测及管理难度大，所以存在数据精确性不高等问题[6-9]。

数值模拟手段在岩土工程方面已经广泛应用。相比现场与室内试验而言，数值模拟具有很大的优势，一方面，成本低，可以多次重复试验，而且开展不同条件下的模拟，找出最合理的参数；另一方面，可以得到任意时刻的位移与变形，可以进行深层次的研究[10-11]。孔汇川[12]利用FLAC3D软件对深基坑施工过程进行数值模拟并对深基坑稳定性进行分析，秦浩等[13]利用FLAC3D软件对受降雨入渗后边坡的稳定性进行分析，李一凡等[14]采用FLAC3D软件对煤矿开采沉陷预计过程进行研究，朱安龙等[15]基于FLAC3D软件对让压锚索边坡的加固机理进行数值模拟研究。所以FLAC3D软件在模拟计算深基坑和边坡稳定性、煤矿开采的沉陷、压锚索边坡加固机理等方面有着广泛的应用。关于利用FLAC3D软件计算基础桩承载力的课题，目前研究的较少。李坛等[16]利用FLAC3D软件对夯扩CFG桩复合地基承载性能进行了研究。在桩顶荷载值分析计算过程中，FLAC3D软件采用显式“拉格朗日算法”和“混合-离散分区技术”等来进行迭代计算，模拟结果相对于其他的软件更加合理与精准，因此本文用FLAC3D软件对大直径钻孔灌注桩桩基础进行模拟[17-20]。

以往的数据及资料显示，扩底桩具有提高桩基础的承载力，增加桩体与土体之间侧摩阻力等优点，被广泛应用[21-22]。本文基于大连市西岗区某工程的实际资料采用的普通桩，利用FLAC3D软件对普通桩与相同直径扩底桩、缩小直径扩底桩桩基础进行模拟，对比分析桩顶承载力与位移量曲线，对扩底桩进行优化设计，进而得出即可以提高承载力又可以节约材料的桩体设计方案；并通过模拟分析，为类似工程的设计提供理论依据，在施工方案上提供经验上的指导。

1 模拟原理

FLAG3D(Fast Lagrangian Analysis of Continua)是由ITASCA公司研发，运用三维有限差分程序的方法，对岩石、土体等介质上的三维受力点进行模拟计算的软件。FLAG3D在分析受力情况时，必须建立有限差分网格，得到材料特性与本构关系式及边界条件等参数[9-12]。

在分析受力过程中，FLAG3D 使用了混合离散的方法。简单来说，把众多常应变六面体看作角点常应变四面体的集合，四面体单元结构如图1所示。我们只需要计算四面体单元应力、应变等变量，然后用四面体的加权平均值计算六面体单元的变量值。

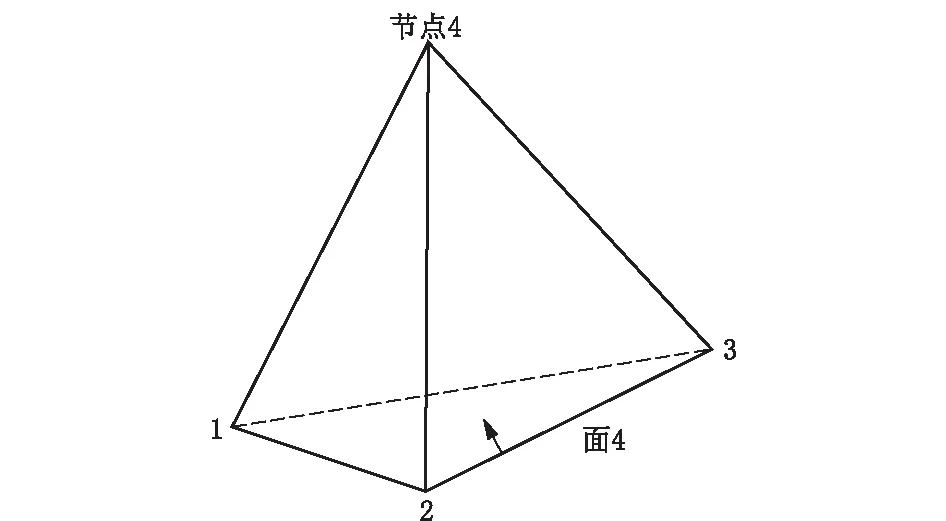
图1 四面体单元Fig.1 Tetrahedron element

假设在四面体单元内的速率分量为Vj，由高斯定理可知：

(1)

式中:V——体积；s——表面积；nj——外表面单位法向量的分量，由于线性分布，nj为常量。

(2)

式中：1——点上应变；(1)——面上应变。

节点运动方程为：

(3)

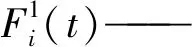
根据中心差分方法近似可得：

(4)

Δeij=1/2(Vi，j+Vj，i)Δt

(5)

通过式(5)，可以得出应变增量，进而计算出应力，根据求解的循环语句得到模拟结果图及数据[9]。

2 模型的建立

2.1 边界条件

本文将土体设置为Mohr-Coulomb模型，桩体设置为Elastic模型，对桩体与土体共同作用的位移场和应变进行模拟[19]。由于模型与桩体范围差别较大，模型采用周边侧向约束的边界条件，即模型底部及周侧约束，模型顶部(z=24的平面)为不受约束的自由面[13-17]。通过应变增量函数求出总应力,进而得出下一时步节点的不平衡力大小，并开始先一步计算。使振动可以逐渐衰减到零的平衡状态，此次模拟引入非粘性阻尼，并采用0.8的阻尼系数。

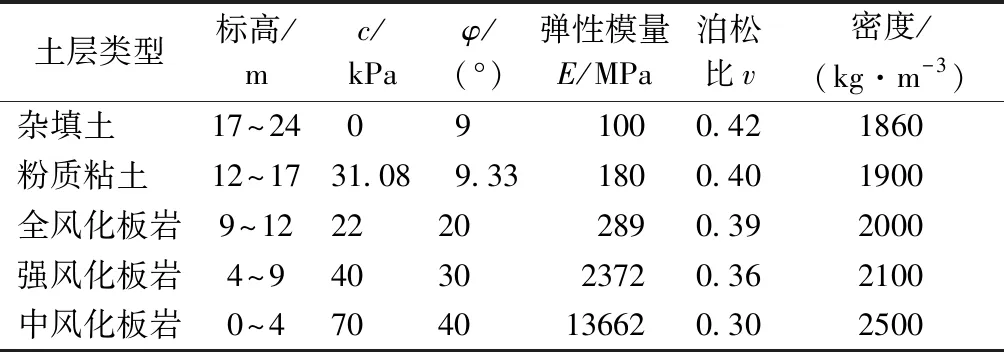
本文选取大连某工程中桩基资料和数据，桩端持力层为中风化板岩、强风化板岩，根据钻探资料，场区第四系覆盖层厚度5～20 m[9]。桩的混凝土强度等级C40，单桩竖向抗压承载力极限值为11000 kN。工程采用的混凝土灌注桩桩径为0.8 m，桩长16 m，土体与桩体的物理力学参数如表1和表2所示。体积模量K和剪切模量G通过勘察报告中土体的变形模量E和泊松比v来确定，转换关系如下：

K=E/〔3(1-2v)〕 (6)

表2 桩体物理力学参数Table 2 Physical and mechanical parameters of piles

2.2 桩基础模型

根据实际资料，本文建立了土体与桩体都存在的模型，其中土体直径为8 m×8 m×24 m，土体类型为杂填土、粉质粘土、全风化板岩、强风化板岩、中风化板岩。内嵌的圆柱桩体类型选取普通桩、相同直径扩底桩、缩小直径的扩底桩3种模型进行模拟，其尺寸如表3所示。

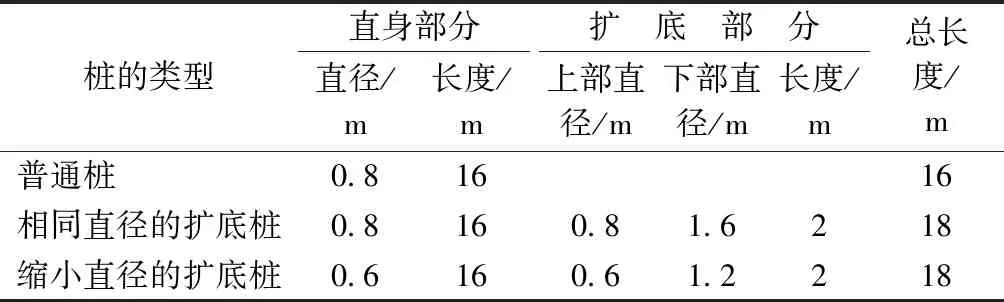
表3 桩体的尺寸Table 3 Dimensions of piles

根据表3中的桩体尺寸，本文建立了3种桩基础的模型：其中普通桩初始模型以坐标(4,4,12)为中心，坐标(1,1,0)为法向量的截面，如图2所示；相同直径扩底桩初始模型以坐标(5.4,5.4,12)为中心，坐标(1,1,0)为法向量的截面，如图3所示；为了区分相同直径扩底桩模型图，本文给出相同直径扩底桩与缩小直径的扩底桩桩体的对比图，如图4所示。

图2普通桩基础的基本模型图3相同直径扩底桩基本模型
Fig.2Basic model of conventionalFig.3Basic model of bell-out pile foundation pile with the same diameter

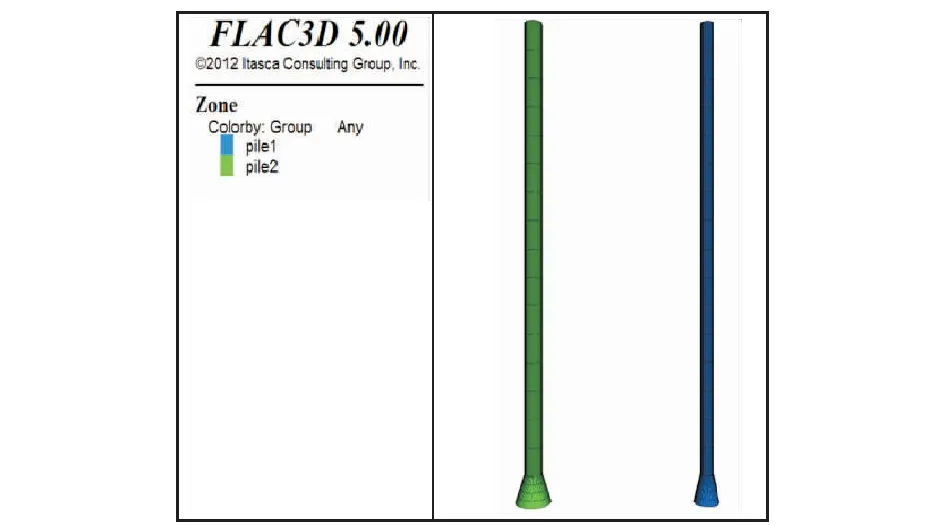
图4 相同直径扩底桩与减小桩径扩底桩模型对比Fig.4 Model comparison of the same diameter bell-out pile and the reduced diameter beel-out pile

3 模拟结果对比分析

3.1 自重应力条件下的结果对比分析

自重应力下普通桩模型最大不平衡力经过约450000时步缩小至0.000001，最终模型整体基本达到平衡状态，得到图5所示的云图。而根据已经建立的相同直径扩底桩模型，当重力加速度为9.80 m/s2时，经过大约744000时步运算，此模型达到平衡，得到图6所示的云图。进而本文对初始的应力场与位移场进行分析。

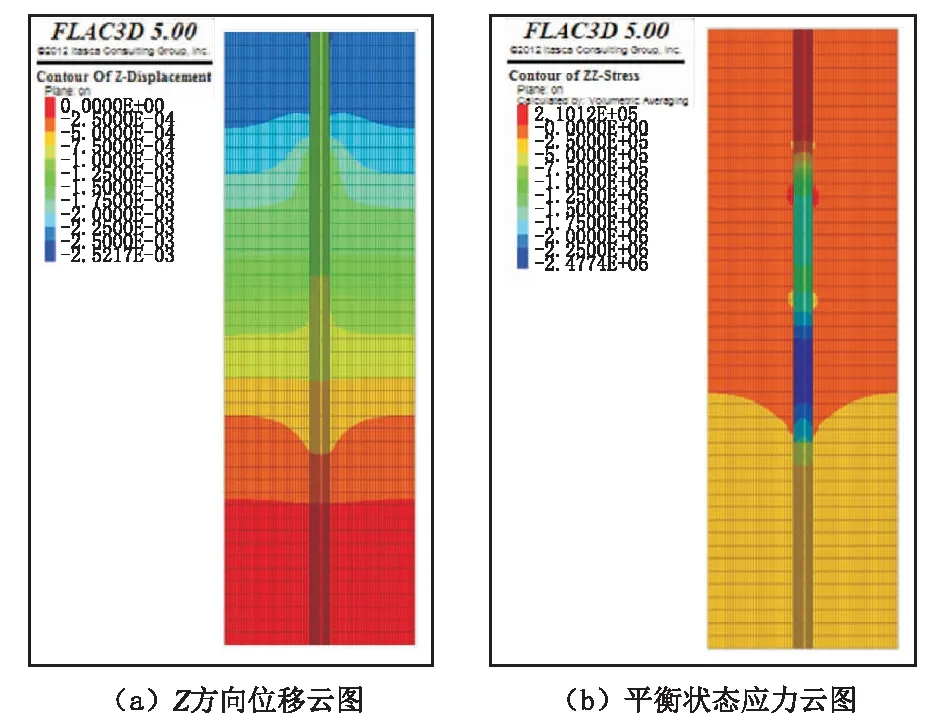
图5 普通桩在自重应力条件下的云图Fig.5 Cloud diagram of conventional pile under gravity stress condition

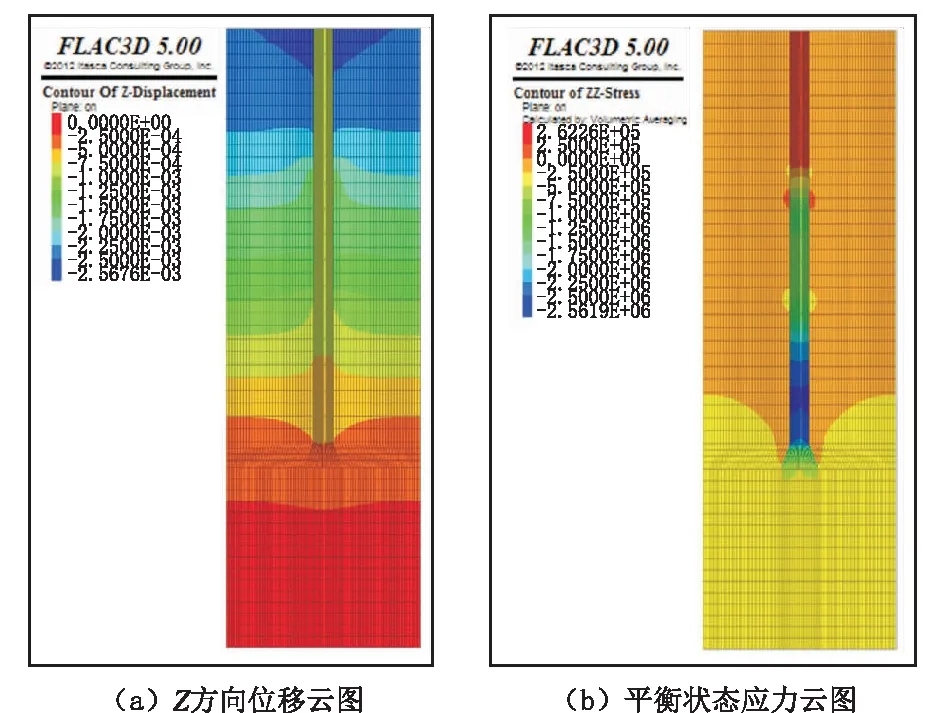
图6 扩底桩在自重应力条件下的云图Fig.6 Cloud diagram of bell-out pile under gravity stress condition

图5(a)为在自重应力条件下普通桩桩基础模型Z方向位移云图。由图可知，在自重应力下模型达到平衡时，沉降量约为2.5 mm。由于桩周边存在摩擦力，桩身和桩周围土体自上而下位移量逐渐减小；加之底部持力层为风化板岩，属于基岩，所以Z方向的位移量极小。所以可以认为桩体上部位移量约为1.35 mm，下部约为1.15 mm。

图5(b)为在自重应力条件下普通桩桩基础模型平衡状态应力云图。由图可知，桩身应力从上到下先变大后变小，表明桩周存在的侧摩阻力是支撑其稳定性的主要因素；由于在下部侧摩阻力没有完全发挥，导致其应力逐渐减小。

图6(a)为在自重应力条件下相同直径扩底桩桩基础模型Z方向位移云图，在自重应力作用的条件下，扩底桩本身位移量约为1 mm，桩周土体的位移量由上到下逐渐减小，且在扩底部分没有产生位移突变，说明相同直径扩底桩桩体与土体有很好的结合作用，同时证明了模型在自重应力条件下处于稳定状态。

图6(b)为在自重应力条件下相同直径扩底桩桩基础模型平衡状态应力云图。桩身Z方向应力从上到下呈现先增大后减小的现象，桩底的应力较小，大约为750 kPa，桩体应力最大的地方位于标高为14～15 m之间，应力约为2562 kPa，说明扩底桩桩身的侧摩阻力没有发挥到极限。因此在实际制桩的过程中，我们需要重点注意标高在14～15 m范围内的桩身质量，保证桩身安全。

通过对比图5(b)与图6(b)可知，在自重应力条件下，普通桩和相同直径扩底桩的侧摩阻力均未达到极限值，这与实际情况相吻合。说明我们建立的模型可以用于此次工程。而且在应力曲线中均有最大值，这就为我们检测桩的好坏位置选取提供依据。通过对比图5(a)与图6(a)可知，在自重应力条件下，普通桩桩身整体位移略大于扩底桩桩身的整体位移。说明在大连此工程处的地层下，相同直径扩底桩相对于普通桩具有较大承载力。两者的位移量相近，所以建立的普通桩与相同直径扩底桩模型与实际工况相近，建立的模型较为准确，模拟结果准确可靠。

3.2 加载结果对比分析

为了使得到的加载结果准确，本文利用循环代码程序实现加载过程。以2000 kN作为加载单位逐渐在桩顶施加荷载，共施加12级荷载，生成的图像如图7所示。图7中纵坐标代表桩顶的位移量，横坐标代表桩顶受到的应力。桩顶横截面积为0.5013 m2，我们将面积近似认为是0.5 m2。为了得到实际桩顶荷载值，我们用横坐标的数值乘以面积，便可得到普通桩模拟桩顶的荷载-位移曲线。实测资料显示，以2200 kN为初始值，以1100 kN为梯度值，对普通桩桩基础的承载力进行试验，得到不同荷载值所对应的位移值，如表4所示。为了方便对比分析试验与模拟结果，得到模拟值与实测值的荷载-位移曲线，如图8所示。为了发现桩体的破坏，本文认为当位移迅速增大时，说明桩结构发生了破坏，此时桩顶施加的荷载定义为极限荷载。

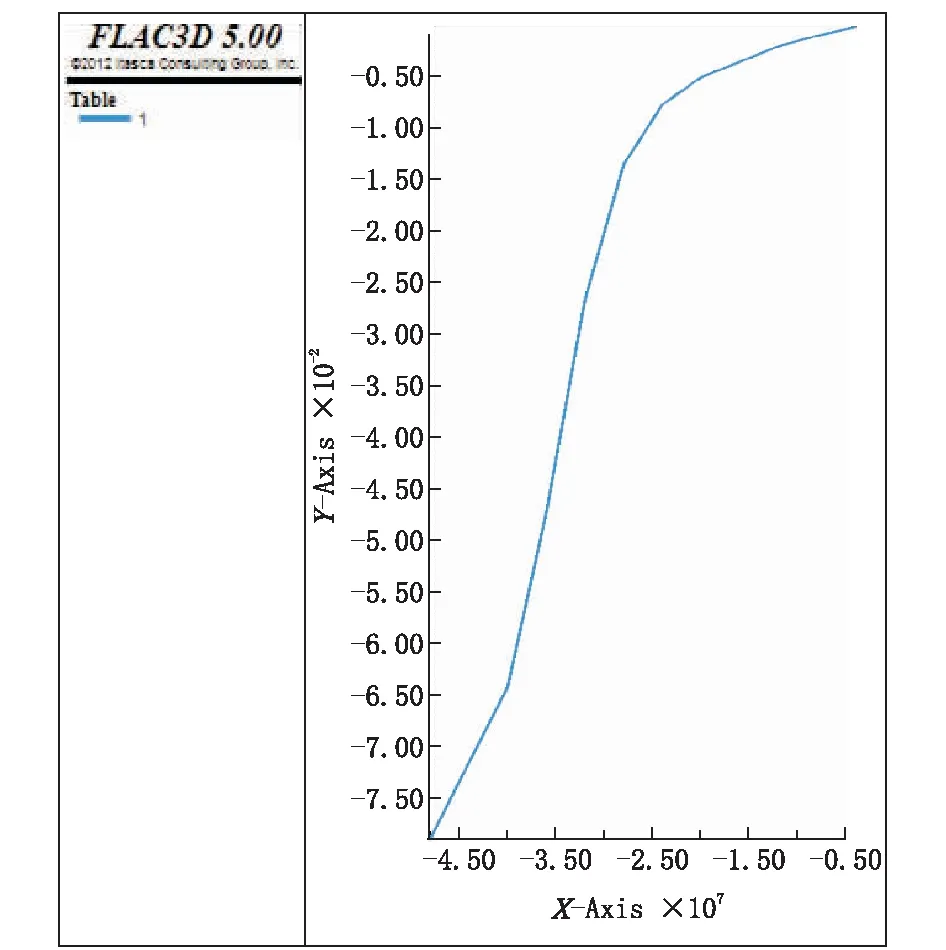
图7 普通桩荷载作用下桩顶位移曲线Fig.7 Displacement curve of pile top under loading for conventional pile

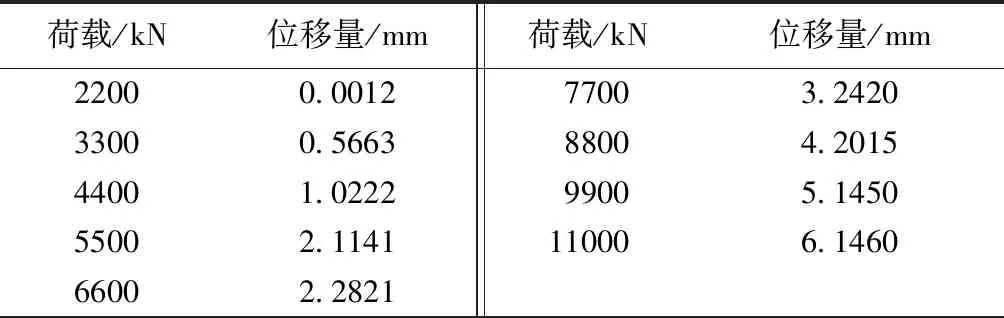
荷载/kN位移量/mm荷载/kN位移量/mm22000.001277003.242033000.566388004.201544001.022299005.145055002.1141110006.146066002.2821

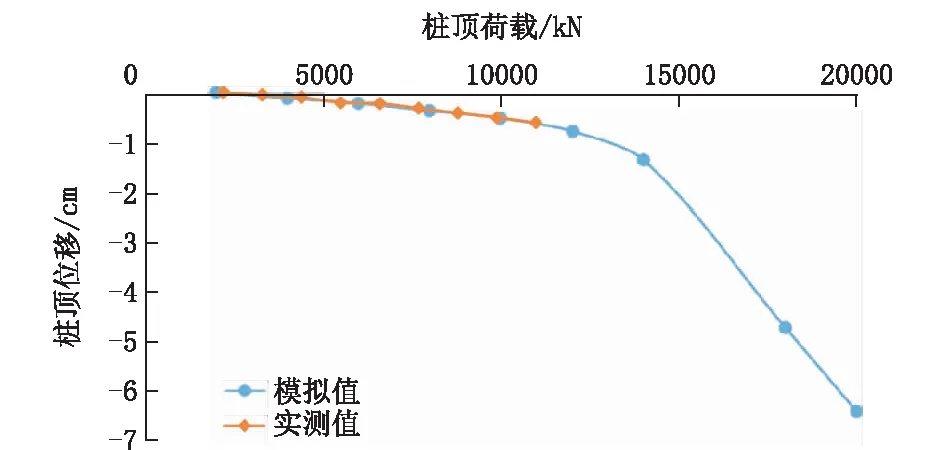
图8 普通桩模拟值与试验值Q-s曲线对比Fig.8 Simulated vs test Q-s Curves for conventional piles

由图8的Q-s曲线可知，模拟值与试验值都随着横坐标值增加纵坐标值也在不断增大，说明位移量的大小与桩顶荷载呈正相关。根据模拟曲线可以得出桩顶荷载值在14000 kN内时，Q-s曲线的斜率基本不变，说明桩与土体在相互作用时，前期随着桩顶荷载的增加，位移量在均匀增加；当荷载值由6000 kN变为8000 kN时，位移量由22.3 mm变为37.6 mm，斜率值大约为7.6×10-5。当Q-s曲线的斜率值突然产生突变，说明桩正在由稳定转化为失稳状态，为了方便描述及记录桩达到的荷载值，笔者将Q-s曲线中横坐标值突变点作为桩的极限承载力；当桩顶荷载为14000 kN时，其位移值为13.69 mm；而桩顶荷载为16000 kN时，桩顶位移值为26.81 mm；其斜率值大约为6.56×10-4。在此过程中桩顶处突然增加了约13 mm的位移量，即桩沉降量约13 mm。说明在14000 kN以后，其斜率值相对前期增加了一个数量级。我们不难发现，此阶段的位移量对上部建筑物的稳定性产生较大影响，因此把14000 kN作为模拟本工程使用的桩最大承载力。根据试验值的曲线，我们可以发现荷载值在11000 kN之内时，曲线呈直线上升趋势，斜率值基本不变，说明在荷载值增加的过程中，位移量均匀增加，桩没有发生破坏。通过载荷试验得出试验值曲线与模拟值曲线，两条曲线拟合的程度很高，说明FLAC3D软件此次模拟桩基础的单桩荷载值较为精确。

实际工程资料显示，在此项目中设计桩体受到的荷载值最低为6000 kN。因此本文得出6000 kN荷载下的模型，进一步分析其受力状态,并得到普通桩和相同直径扩底桩的应力云图，见图9。

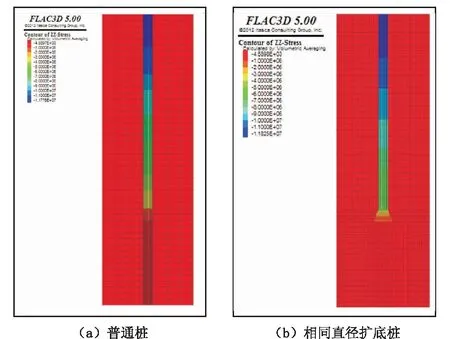
图9 6000 kN荷载下的应力云图Fig.9 Stress nephogram under 6000kN load

由图9(a)6000 kN荷载下普通桩的应力云图可知，桩顶应力为11776 kPa，桩端应力约为4000 kPa；由图9(b)6000 kN荷载下扩底桩的应力云图可知，桩顶应力为11825 kPa，桩端荷载2000 kPa。两个图均出现桩身的Z方向应力从上到下逐渐减小的现象。这是由于当荷载为6000 kN时，由于土体与桩体相互作用的影响，桩身的侧摩阻力已经完全发挥作用且达到极限，桩端阻力开始承担一部分荷载。当在自重条件下荷载时，发现桩身的侧摩阻力还没有达到极限，桩端没有承担应力。因此本文得出随着荷载值的增加，桩身的侧摩阻力是逐渐增大，荷载值大于6000 kN时，桩身的侧摩阻力达到极限。

实际的桩设计资料显示，此次的大直径桩的类型属于端承摩擦桩，其目的是增加岩体与土体的摩擦力，减少桩本身承受的荷载值。当在单桩的顶部逐渐加荷载时，桩身会产生压缩，桩的侧面就会产生摩擦阻力，而且摩擦阻力随着荷载压力增加而增大。当侧摩阻力达到最大时，如果荷载继续增加，桩端阻力就会增加，所以会产生上述现象。本次施工选用端承摩擦桩不仅可以减少桩体的应力，而且可以使桩承受更大的荷载，保证施工的安全。

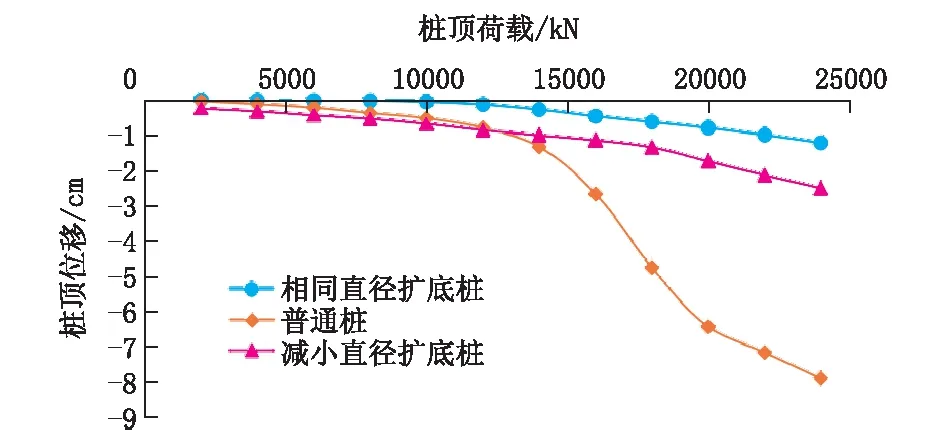
图10 普通桩、相同直径扩底桩、缩小直径扩底桩的Q-s曲线对比 Fig.10 Q-s curves of common piles,bell-out piles with the same diameter and bell-out piles with reduced diameter

根据模拟得出的普通桩、相同直径扩底桩及减小直径的扩底桩的Q-s曲线，绘制出如图10 所示的Q-s曲线对比图。由图可知，当桩顶荷载达到为6000 kN时，其位移值大约为2.23、0.129、4.42 mm，位移值较小；而且此处的斜率基本不变，说明模型处于稳定状态。由此我们可以确定桩处于正常状态下，混凝土灌注桩能够满足实际使用过程中的承载要求。

根据实际情况，本文通过对比6000 kN荷载下的相同直径扩底桩和普通桩，我们可以发现普通桩桩端应力明显大于相同直径扩底桩；这是由于相同直径扩底桩底部面积相对较大，致使其在相同承载力的情况下，应力就相对减小。根据图10可知，普通桩在6000 kN荷载条件下桩顶位移量为2.23 mm，而相同直径扩底桩的位移量为0.129 mm，位移量大约是20倍。通过分析可知，相同直径扩底桩的桩底部位有明显的扩大，这就使桩与持力层的接触面积增大，可以使桩端应力分布更加均匀；同时随着表面积的增加，桩周土侧摩阻力极限值增大，土体与桩体更加充分结合，这就导致相同直径扩底桩的桩底在相同承载力的情况下位移量相对较小。

通过对比分析相同直径的扩底桩和缩小直径的扩底桩曲线可知，桩顶的荷载由2000 kN增加到24000 kN的过程中，相同直径扩底桩桩顶位移量从0增大到12.2 mm，斜率基本没有变化；缩小直径的扩底桩的桩顶位移量由2.51 mm增加到25.15 mm，曲线没有发生突变。说明在过程中没有发生桩体的破坏。当荷载增加到此次模拟的极值时，两条曲线位移量都很小，上部建筑物不会发生失稳现象。因此本文认为相同直径的扩底桩和缩小直径的扩底桩的极限荷载在24000 kN之上。但由于相同直径扩底桩消耗的材料更多，所以缩小直径的扩底桩更优。

通过对比分析普通桩与缩小直径的扩底桩的Q-s曲线可知，承载力11000 kN时，缩小直径的扩底桩的位移量高于普通桩的位移量，这是由于直径及高度的减小，导致桩周与土体接触面积减小，桩体与土体之间的侧摩阻力减小。根据两种类型桩在6000 kN承载力情况下的应力云图得知，此时侧摩阻力刚刚达到极限，随着承载力的增加，桩端阻力作用明显。由于缩小直径的扩底桩的桩底面积大，桩端阻力相对大，所以位移量小，当承载力为11000 kN时，致使位移量近似相等，符合实际情况。缩小直径的扩底桩的Q-s曲线的斜率没有发生变化，而普通桩在14000 kN时发生突变。所以缩小直径的扩底桩的承载力明显好于普通桩。通过公式计算，缩径后扩底桩的体积约为19.7 m3，而普通桩的体积约为32.2 m3，每根桩相对减少12.5 m3的混凝土，其用料占普通桩的61.2%，在很大程度上降低成本。通过与柱基础设计规范对比，缩小直径的扩底桩在尺寸等方面均符合要求。

为了保证以后施工工程的安全、桩基础稳定、节约成本等，根据模拟结果显示，本文建议采用圆柱部分直径为0.6 m、高为12 m，扩底部分上直径为0.6 m、下直径为1.2 m、高为2 m的缩小直径的扩底桩。对原有的设计进行修正并为以后的类似工程提供理论依据。

4 结论

(1)利用FLAC3D软件模拟了普通桩Q-s曲线变化，在相同荷载下，通过工程实测的位移值绘出Q-s曲线与模拟曲线基本吻合，说明建立的FLAC3D模型比较适用于本工程问题研究。

(2)利用建立的FLAC3D模型对在6000 kN荷载、直径相同的条件下的扩底桩(桩的直身部分直径)和普通桩进行受力分析，普通桩桩顶应力为11776 kPa，桩端应力约为4000 kPa；扩底桩桩顶应力为11825 kPa，桩端应力2000 kPa；在6000 kN荷载下，桩端应力减少50%，改善了桩端受力条件。

(3)在桩长不变的条件下，研究了缩小桩径的扩底桩的承载力，其用料占普通桩的61.2%，模拟结果表明能够达到工程荷载要求，并且降低了成本。建议对原有的设计进行修正并为类似工程提供理论依据。