应用归纳法确定“三位数乘两位数”的最大值
□ 钟家卫 朱挺红
人教版教材四年级上册第50页第12题是一道思考题:“用0,2,3,4,5组成三位数乘两位数的乘法算式,你能写出几个?你能写出乘积最大的算式吗?”解决这一问题有怎样的思路?又会有什么规律呢?利用怎样的策略让学生自主发现这一个规律呢?更进一步,在5个数字中出现相同的数字时,发现的规律是否同样适用呢?带着这些问题,笔者进行了教学实践研究。
一、尝试猜想,提出假设
教材第12题中5个数字里面出现了0,填在数的末尾在竖式计算时可以简便计算,这会影响规律的发现。同时,题目没有说明是否可以重复用某一个数字,容易产生歧义。因此,我们把题目改为:用1,2,3,5,6组成三位数和两位数的乘法算式,每个数字用且只用一次。这样的乘法算式可以写出许多个,猜一猜,乘积最大的算式可以是怎样的?
(一)直觉猜想,比较归类
提出问题后,学生会依据原有经验做出猜想。把大的数字填到最高位是学生应有的想法。由于初次尝试,会有不同的答案。如:(1)653×21,(2)631×52,(3)532×61,(4)521×63。教师板书以上几个算式。然后提问:黑板上已经有4个算式了,请你估一估,哪个算式一定不正确,为什么?
生:第1个算式一定是错的,把650估成700,21估成20,700×20=14000。另外的几个估算的结果都是30000。
师:说得有道理,那么后面的3个算式哪一个算式的积最大呢?
生:那要算一算。
生:我觉得只算这3个还不够,我写的算式不一样,但估算的积也是30000。
师:说得很棒,想一想,仔细观察估算的积是30000的3个算式,有什么共同点?在竖式中(如图1)填一填你发现的规律。
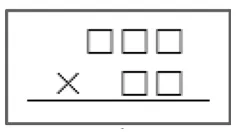
图1
学生独立填写后反馈交流,填出了如图2的两种情况。
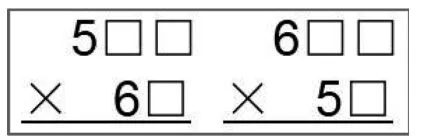
图2
从个体猜想到集体反馈,用估算的策略构建起积最大值的两种基本模型。这是培养学生从纷繁复杂的数学现象中发现规律,构建数学模型的基本方法。
(二)枚举可能,分组计算
依据构建起的两种基本模型,进行有序思考,用枚举法补全所有可能的算式。按小组分工计算后,教师出示图3进行校对。

图3
同样是计算题,由于带着探究规律的目的,计算有了思考的价值,有利于激发学生的计算兴趣。
(三)观察分析,初步猜想
校对后,请学生比较积的大小,用图3中的虚框,圈出积最大的数,然后引导学生观察分析,积最大的两个因数有什么规律。
生:最大的数字填在两位数的十位上。
生:两位数是由最大的数字与第二小的数字组成的。
从猜想估算到枚举计算,从比较发现到提出假设,这是探究数学规律的基本步骤之一。教师在提供合理的学习材料的同时,要设计能够促进学生积极思考的问题,让问题探究成为一种内在的需要。
二、举例验证,发现规律
从一个例子中获得的结论,需要通过更多的例子进行验证,这是用归纳方法进行合情推理需要经历的过程。
(一)举例验证,积累经验
教师再次出示一组数据,提问:用1,3,5,7,8,同样要求组成积最大的“三位数乘两位数”算式,你能够直接找到吗?因为有前期探究的经验,大多数学生都认为是751×83。这时,教师质疑:一定是这个算式吗?如果要验证,那可以怎样做?
生:把所有的情况都列举出来,然后算一算,比一比,积谁最大?
生:不用全部举出来,只要模仿上面的例子,写出其中的6个算式,然后算一算,比一比。
学生列出其中的6个算式,然后与前面例子一样分组计算后校对(如图4),发现猜想是正确的。
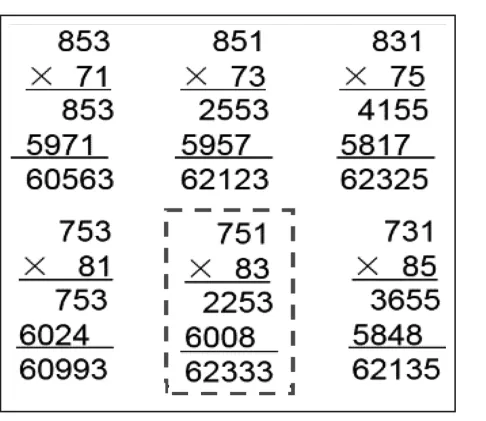
图4
(二)小组举例,合作验证
通过两个例子的学习,学生已经初步确定这一个规律是正确的。但是,从科学严谨的角度看,应该举更多的例子进行验证,规律的正确性就会提高。因此,教师要求以小组为单位,首先任意选5个不同的数字,然后列举出同前面例子形式相同的6个算式,再分工计算,验证假设。
由于是带着探究的目的进行计算,学生在计算时更容易集中注意力,在分工合作的过程中相互帮助,互相指正。
(三)比较分析,发现规律
教师展示各小组选出的最大积的两个因数组成的竖式。然后引导学生再次观察,并用箭头把5个数按从大到小的顺序连一连(如图5)。学生发现有共同点后,教师要求学生在竖式模型(如图6)中连一连,得到图7。
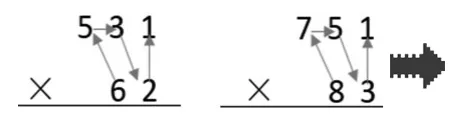
图5
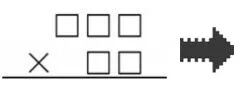
图6
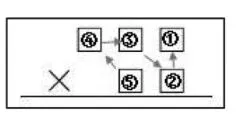
图7
在寻找“积的最大值”的过程中,结合多种计算形式,通过比较归纳获得了求“积的最大值”的填写规律。在这样的过程中,学生学到的不仅仅是一个结论,更经历了探究数学规律的过程,培养了自己的数感。
三、变式练习,形成技能
填写“积的最大值”的规律在数据特点发生变化时是否可行?如果改为求“积的最小值”是否也有规律?基于这两点,教师进行了变式练习的设计与教学。
(一)当出现一个零时
书本原来的题目中,5个数字中有一个0,我们把这类问题称为其中的一种变式。教师出示问题:把0,2,3,4,5组成一个三位数与两位数,每个数字只能够用一次。要使积最大,算式是( ),最大的积是多少?
先请学生观察并说一说这组数据与前面列举的5个数字有什么不同的地方,原来的规律是否还成立。学生在小组内枚举可能的算式,分工合作完成,发现原来的规律仍然可用。
这一类情况如果在前面一个教学环节——小组举例时已经出现,那么可以在之前学习时讨论总结。
(二)当出现重复数字时
5个数字中如果出现两个数字相同时,原来的规律是否也成立呢?教师出示两组数字,第一组是5,2,2,1,6;第二组是0,0,7,6,9。请学生先判断,找出自己认为积最大的算式。以小组为单位验证其中的一组,完成后汇报。验证后发现,原来的规律还是成立的。验证的过程,是计算练习的过程,也是培养学生逻辑思维的过程。
(三)求“积最小值”的算式
如果把寻找“积最大”的三位数乘两位数改为“积最小”的三位数乘两位数,是否也有一定的规律呢?能用前面的学习活动经验来解决这一问题吗?
教师出示题目:用5,6,7,8,9组成三位数和两位数的乘法算式,每个数字只用一次。猜一猜,乘积最小的算式是怎样的?
师:这个问题与前面研究的问题有什么不一样的地方?
生:现在积要求是最小的。
师:根据前面的经验,这个三位数乘两位数可能是哪两种竖式的形式?
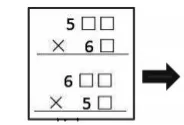
图8
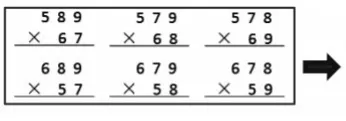
图9
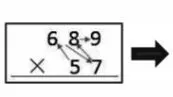
图10
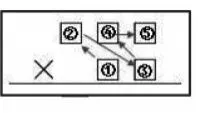
图11
依据学生的回答总结出如图8两种形式,接着分别填出6种可能(如图9),并请学生猜一猜哪一个竖式的积会最小。然后分工计算并找到积最小的算式,最后标出5个数从小到大的排列规律(如图10)。在以上活动的基础上形成猜想(如图11)。为了验证猜想是否正确,再让学生举例验证,总结出规律。总之,当计算练习转化成规律探究,可以让原本枯燥的计算变成有趣的猜想验证。在这样的过程中,得出规律并不是主要的目的,重要的是探究的过程。因此,教师要精心设计活动环节,提出问题、发现问题、分析问题与解决问题有序展开,并能主动回顾提炼问题解决问题的过程,获得数学活动经验,应用于类似的数学探究之中。

