数学教学 理解先行
刘思武
摘要 数学教育的目的不仅仅是教授学生知识与技能,更是教会学生发现知识之间的内在联系。要达到这一目的,数学教师就要理解数学的本质,熟知每个知识点之间的联系,整体思考问题,从细处去理解知识点。教师多思多读,让学生收获的不仅仅是细小的知识点,还有数学思想、数理逻辑。
关键词 数学概念 理解数学 稳定性
章建跃教授提出的“理解数学,理解学生,理解教学”中,第一个理解就是让教师要理解数学,这是数学教师必须做到的。教师理解数学是提高教学质量的前提,在此基础上才能谈理解学生,理解教學,践行培养学生的核心素养,才有可能发挥数学的育人作用。
苏科版数学教材八年级第一章就是全等三角形,其中判定方法“SSS”之后提出了三角形的稳定性。一讲到稳定性,那从小学就开始讲了啊,学生还能不知道,不就是拉不动嘛!哦,是吗?还真的有爱思考的学生提出了质疑:当四根钢条周围焊接起来也是拉不动的,当三根皮筋构成三角形,它的形状是能够改变的呢!这里为什么出现大部分学生认为稳定性就是拉不动,教师又是如何理解的呢?这值得思考,让我们深入探究一番。
关于三角形的稳定性,小学教师在备课时是怎么想的呢?三角形的稳定性为什么在给出“SSS”时提出呢?没有真正的理解估计就很难把握其本质,更不用说理解学生、理解教学,所以章建跃教授在三个理解中将理解数学放在第一位是有所思考的,这为教师的自我提升提供了方向。
一、三角形稳定性的内涵
李邦河院士曾说,数学是需要玩概念的,而理解数学概念就要做到从表面到本质达到结构上的一种进步。三角形的稳定性到底是什么呢?这里有两个关键词,三角形和稳定性。一般来说,稳定性是指不易改变或保持其原有属性的能力,稳定性又可以分为结构性的、系统的、过程的三种。回到三角形的定义:三条线段首尾相连所围成的封闭图形。这种连接是铰链,而不是焊接。四边形的不稳性也是因为铰链可以随着外力的作用而“变形”,所以了解这个就让学生知晓即使梯子包含了四边形却为什么是“稳定”的,这个稳定性是物理层面的,指在外力作用下形状不变,因为这个图形的四边都是固定连接,涉及物理中受力和材料性质的分析。
几何图形中的稳定性是指几何图形形状的确定性,当三边确定后,三个角的大小就确定了,也就是形状、大小就跟着确定下来。即已知三边得出三角形的三个角,从而面积、周长也就确定了,三角形的这种属性就叫做三角形的稳定性。从三角形出现,这个性质就存在了,与有无外力拉动毫无关系,如由三根棉线构成的三角形在外力的作用下“稳”吗?所以三角形的稳定性更多的是“定”,即唯一性。
数学教师应该拥有的一项基本功是举例子。通过研究,笔者发现平时我们经常论及三角形稳定性在生活中的应用的例子有些是不合适的。在学习了三角形的稳定性之后,教师会让学生举一些生活中相关的例子,即三角形稳定性的外在表现。有学生会以三脚架为例,其实深入研究之后,发现原来三脚架的选择不是因为三角形的稳定性,而是从物理的受力分析、节省材料以及携带方便等角度来考虑的。没有研究就没有发言权,理解数学本质是数学教师需要首先做到的。
二、三角形稳定性的数学证明
三角形的稳定性还可以通过实验验证,数学概念应更多地回归到数学解释上,即本质的探究。
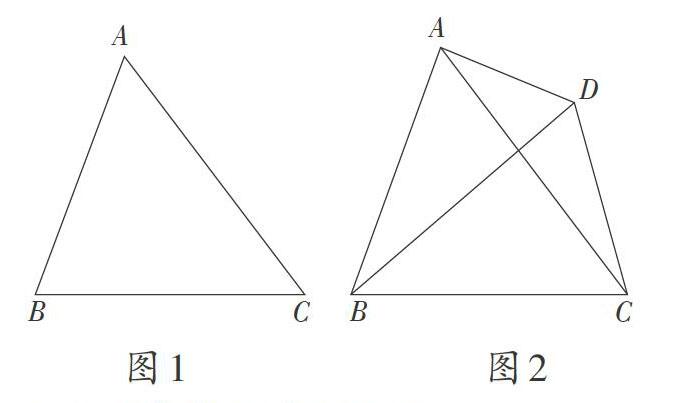
已知:如图1,在△ABC中,BC=a,AC=b,AB=c。
求证:△ABC的形状大小确定。
解析:要证明三角形的形状大小确定,即证明△ABC的三边确定。我们不妨假设角的大小不确定,即存在一个三角形与△ABC三边分别相等,但是对应角不相等。为了操作方便,按照图2进行构图,BA=BD,CD=CA,假设∠BAC≠∠BDC。连接AD,因为AB=DB,则∠BAD=∠BDA。由于AC=DC,则∠CAD=∠CDA。因为整体大于部分,所以∠ADC大于∠ADB,由此∠CAD大于∠BAD,这与整体大于部分相矛盾,从而假设不成立,即∠BAC=∠BDC。
三、理解数学的教学意义
理解数学概念,深入到数学内部就能够真正弄清楚数学知识的内在联系。数学教育的目的不仅仅是教授学生知识与技能,更是教会学生发现知识之间的内在联系,构建一种知识结构,形成全局观,看待问题能够有一种高位认识,从而真正培养学生思考的习惯,以便将来进入社会即使忘掉所有的数学知识,但是用数学的眼光看待问题、用数学逻辑解决问题的能力仍然不会遗忘。因此,我们教师首先要理解数学,抓住本质,熟知每个知识点之间的联系,整体地思考问题,从细处去理解知识点,并且能够生发出一幅幅巨大的知识网,这一幅幅巨大的知识网汇聚在一起最后就形成了数学的大厦,真正能够让学生受益终生。
理解数学说起来容易,做起来难,作为教师首先要有深入的思考,能够理解教材的章节设置,深悟其中的逻辑合理性,从而在教学中才更有发言权。在进行教学设计时能够更加符合数学的内在联系,让学生收获到高于知识点之上的东西:数学思想!如,在进行勾股定理教学设计时,是不是该研究直接给出三边的平方关系是否合理?是否该考虑该章节在整个教材中的地位,放在整个知识框架中里去思考?是否应该重新设计,让学生慢慢探索两条直角边与斜边的关系,让学生多一点探究,才更能够体现数学的味道?为什么一元二次方程有时叫做解,有时叫做根?三角函数以前用线段的比来定义,现在为什么又叫做三角函数呢?虽然有些概念是规则下的定义,但是细细思考还是很有味道的,能够发现数学的发展史。随着研究的不断深入,或者带着问题去研究,你会得到更多的乐趣,这可能就是探究的乐趣。孙子兵法:求其上,得其中;取其中,得其下;求其下,必败。这句话用在教师对数学的理解上也很有启发。教师高位理解数学,进入到数学内部,才能有高效的教学。
(作者单位:南京外国语学校仙林分校燕子矶校区)

