低含液输气管道内液滴时空分布特性的数值研究

管 孝 瑞

(中国石化青岛安全工程研究院 化学品安全控制国家重点实验室，山东 青岛 266071)

0 引 言

低含液率是指每百万标准m3(101.3 kPa，15°C)气相中含有小于1 100 m3的液相，或者液相表观速度小于0.02 m/s的工况[1]。在天然气开采中，尤其是处于山地丘陵地带时，湿气集输工艺被广泛采用，在集输过程中，由于受到沿程温度、压力的变化，天然气中的饱和水蒸气会发生相变形成液滴，在管线中随天然气运动，进而形成这种低含液气液两相流动。管线内的液滴对于管线压降和持液率影响较大。

随着测量手段的发展，低含液管内气液两相流的实验研究逐渐得到加强[2-8]，实验管路直径从50.8 mm增大到152.4 mm，实验研究内容从“压力梯度、持液率[2]”深入到“湿周、液膜厚度[3]、雾沫夹带[5]、液膜速度[7]、界面波特征[8]”，但受限于测量仪器，无法对管内流动特性进行详细分析，尤其是输气管道内液滴群的空间分布以及随时间的变化特性还需进一步开展研究。近年来，数值模拟技术在流体力学领域发挥了重要作用[9-10]。

在前期的实验[11]中，利用瞬时局部液膜厚度测量系统对管线内液膜厚度分布特性进行了研究。本文利用CFD软件对实验管路进行数值研究，考虑不同粒径的液滴群，获得管内气相流场、液滴群空间分布及随时间的变化特性。

1 几何模型与网格划分

1.1 几何模型

管路布局及尺寸如图1所示，坐标原点位于管路入口，重力指向-y方向。管道直径d=90 mm，选取集输管路中常用的桁架结构，包含上水平管4 m、上90°弯头(曲率半径Rc=120 mm)、竖直管630 mm、下90°弯头(曲率半径Rc=120 mm)、下水平管6 m，气液两相由上水平管进入，下水平管流出。

图1 管路布局及尺寸(mm)

1.2 网格划分

管道近壁面处采用边界层网格进行划分，第1层网格高度ds=35 μm，层间增长因子1.5，设置12层，总厚度9.012 2 mm。生成边界层网格后，横截面网格采用pave格式生成，整个管路总网格数922 955。管道横截面、边界层和弯头处网格如图2和3所示。

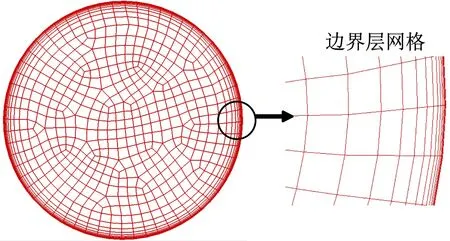
图2 管道横截面网格

2 计算模型

2.1 湍流模型

输气管线内气液两相流处于湍流状态，RNGk-ε模型[12]能够用来模拟管路中的湍流运动：

ρε-YM+Sk

(1)

(2)

μeff=μ+μt

(3)

μt=ρCμk2/ε

(4)

式中:k为湍动能，m2/s2；u为流体流速，m/s；ak和aε为常数，1.393；μeff为有效运动黏度，Pa·s；ε为湍流耗散率，m2/s3；Gk为平均速度梯度产生的湍动能，m2/s2；Gb为浮力产生的湍动能，m2/s2；YM为可压缩湍流中波动膨胀对总耗散率的影响；Sk和Sε为自定义源项；C1ε为常数，1.42；C2ε为常数，1.68；当主流方向平行于重力方向时，C3ε=1；当主流方向与重力方向垂直时，C3ε=0；Cμ为常数，0.084 5。

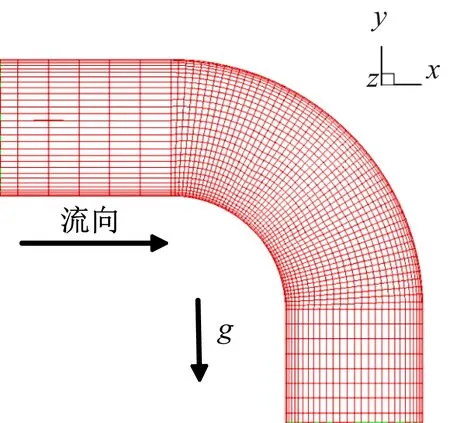
图3 弯头处的网格

2.2 双流体模型

多相流模型选用Euler-Eulerian模型，该模型对气相和液相建立动量方程和连续性方程，通过压力和相间交换系数的耦合进行求解计算，能够对气液两相流动进行精确的模拟。

(1)体积分数方程。第q相的体积Vq定义为：

(5)

(6)

式中，αq为第q相的体积分数。

(2)连续性方程

(7)

(3)动量守恒方程

(Fq+Flift,q+Fwl,q+Fvm,q+Ftd,q)

(8)

式中：τq为第q相的应力应变张量；Kpq为相间动量交换系数；Fq为外部体积力，N；Flift,q为升力，N；Fwl,q为壁面润滑力，N；Fvm,q为虚拟质量力，N；Ftd,q为湍流分散力，N，采用simonin模型；vq为第q相的速度，m/s。

(4)universal-drag模型。universal-drag模型可用于计算多种气液流型中曳力系数，本次模拟中水力直径远大于液体平均尺寸，故采用universal-drag模型。

2.3 边界条件

(1)入口条件。入口边界条件选用Velocity inlet，数值模拟中采用的计算参数如下：Usg=16.68 m/s，ρg=1.225 kg/m3，ρl=1 008 kg/m3，Usl=6.99 mm/s，μg=1.86×10-5kg/(m·s),μl=8.6×10-4kg/(m·s),Resg=98 869,Resl=737,σ=71.9 mN/m。入口含液率为4.2×10-4。设置气相为主相，液相为第二相。

液相以液滴群的形式进入管路，粒径分布与实验管路中入口液滴[11]相一致，如图4所示。最大粒径191.203 μm，最小粒径37.028 μm，比表面积平均粒径d32=109.785 μm。

图4 管路入口液滴粒径分布

(2)出口条件。下水平管长度保证管路内气液两相流动充分发展，管路出口采用自由出流边界条件。

(3)壁面条件。近壁面区域采用增强壁面函数[13]来处理，该函数结合边界层网格适合用于求解近壁面处的低雷诺数流动。模拟结果显示y+<5，满足增强壁面函数使用要求，如图5所示。

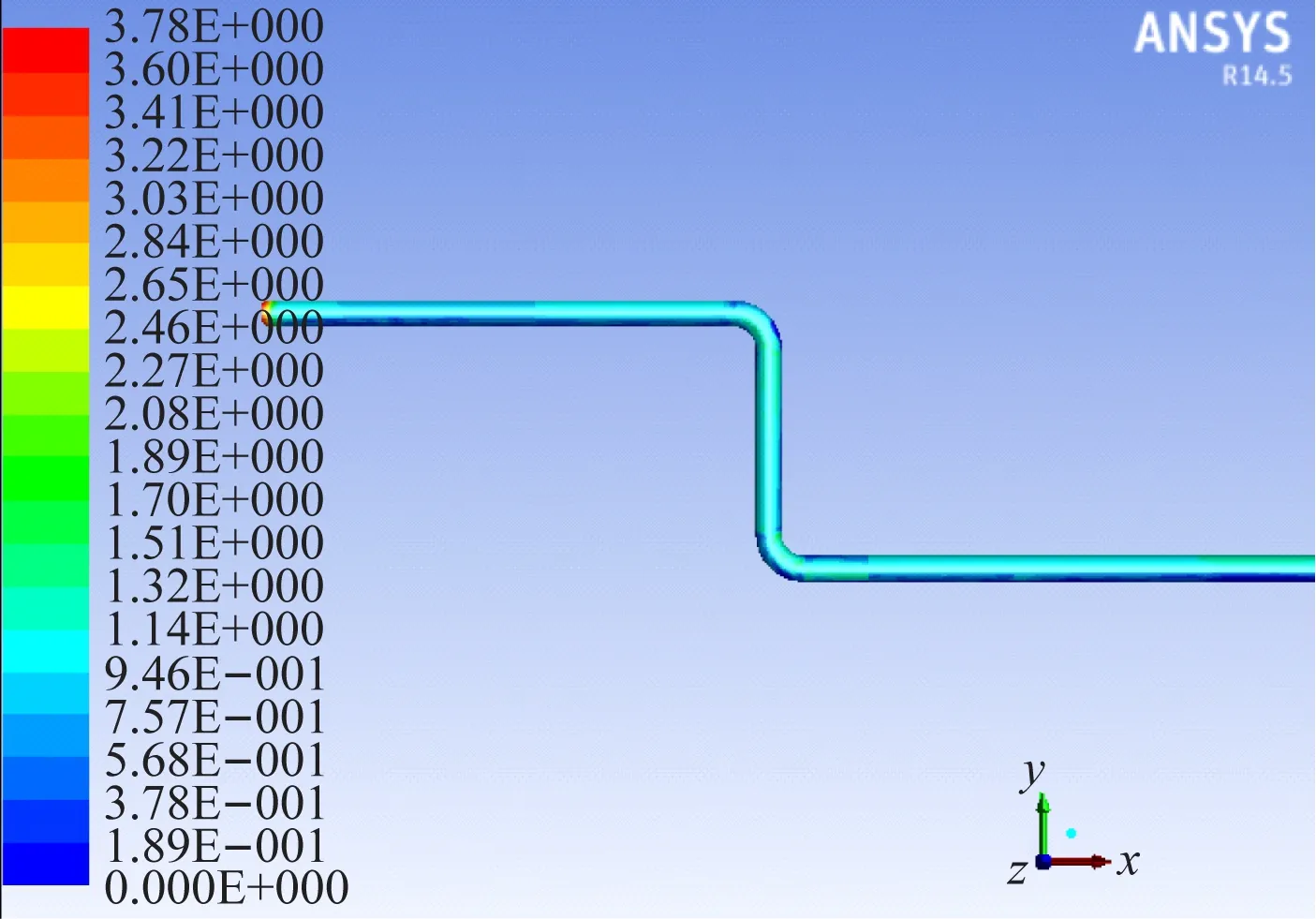
图5 管道壁面y+值分布

2.4 计算方法

采用有限体积法对控制方程进行离散，应用Phase Coupled SIMPLE格式的压力速度耦合，并应用QUICK格式求解体积分数，连续性方程、动量方程、湍动能方程、湍流耗散率方程采用二阶迎风格式求解。

3 断面速度分布验证

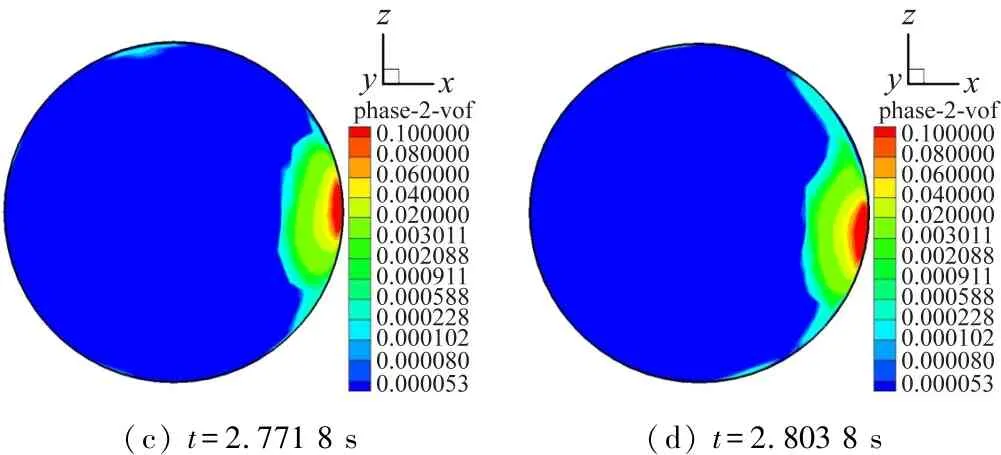
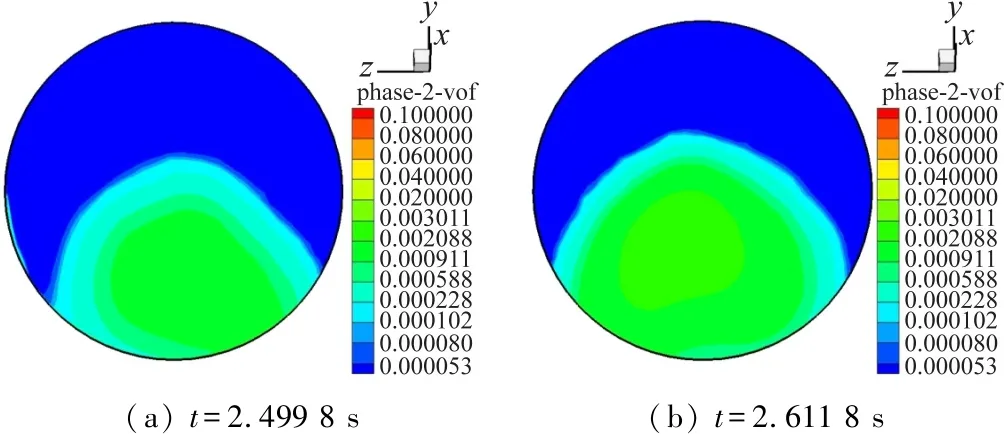
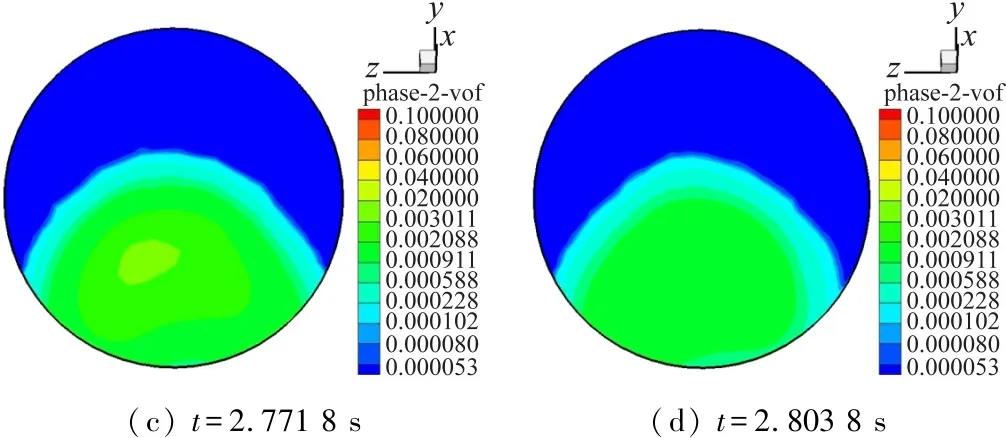
圆管内湍流分为黏性底层、过渡层、对数区[14-15]。在黏性底层内(0≤y+<5)，黏性切应力占主导地位，速度分布对应图6中实验曲线1;在过渡层内(5

图6 水平管x=3 150 mm处流速分布与实验数据对比

4 结果与讨论

4.1 上弯头内气相流场

管路内流体主流方向为轴向，但在垂直于轴向的横截面内也存在流动。图7为上弯头内不同截面处的气相流线，图中红色箭头为离心力方向，指向弯头外侧，重力沿半径方向的分量指向弯头内侧，通过比较可知离心力大于重力沿半径方向的分量，因此合力方向指向弯头外侧，造成中心气相由弯头内侧流向弯头外侧。同时，由于气相的连续性，两侧壁处的气相由弯头外侧流向弯头内侧，因而形成二次流。

(a) 30°(b) 60°(c) 90°

图7 上弯头内气相流场

4.2 上弯头后的竖直管内气相流场

图8所示为上弯头后的竖直管内不同横截面处的气相流场。由于上游弯头内存在二次流，气相进入竖直管后，二次流影响依然存在，竖直管横截面存在一对涡核，沿流动方向，竖直管内二次流的中心由左侧逐渐向右侧移动。

(a) y=-163 mm(b) y=-290 mm(c) y=-679 mm

图8 上弯头后的竖直管内气相流场

4.3 下弯头内气相流场

图9为下弯头内不同截面处的气相流线，红色箭头为离心力方向。下弯头0°截面内气相流场与上游竖直管相似，管道横截面内存在一对涡核，但相比于竖直管y=-679 mm截面，二次流强度减弱。在下弯头30°截面，出现两对涡核，一对靠近壁面；另一对靠近管道中心。在下弯头内，离心力方向指向弯头外侧，与重力沿半径方向的分量一致，随着弯头角度的增大，两者合力逐渐增大，壁面处的涡核逐渐加强扩大，而靠近管道中心的涡核则逐渐被压缩，在下弯头90°截面处，管道只存在一对涡核，原有的靠近管道中心涡核则消失。

(a) 0°(b) 30°

(c) 60°(d) 90°

图9 下弯头内气相流线

4.4 不同位置处液滴群的时空分布特性

图10(a)为通过实验测量[11]获得的该工况下水平管x=3 150 mm截面管壁液膜分布，图10(b)为利用数值模拟得到的该截面处的液滴群时均分布(随时间的平均分布)。从图中可以看出,管内气体、气核中的液滴和管壁上的液膜相互作用，气相和液滴影响着液膜的运动与分布，同时液膜的运动与分布又影响着液滴群的分布，具体体现如下：① 湍流将液滴输送到壁面上，有的液滴会融入液膜中，近壁面处高浓度的液滴群对液膜形成与发展具有很好地补充作用；② 波动的液膜在气相作用下，发生剥落形成液滴，随气相运动到气核中，进而影响着液滴群的分布情况。

(a) 液膜时均分布 (μm)(b) 液滴群时均分布

图10 水平管x=3 150 mm截面处液膜液滴分布

图11为水平管x=3 150 mm截面内液滴群的空间分布及随时间的变化。由于受到重力的影响，液滴群主要集中在管道底部，促进了管路底部液膜的形成与发展。t=2.499 8 s时可以看到液滴分布波动特性，且高浓度的液滴群有向z正方向波动趋势，在t=2.611 8 s时又具有向z负方向波动趋势，在t=2.771 8 s时液滴分布较为对称，而在t=2.803 8 s时液滴又产生了向z正方向波动趋势，且与t=2.499 8 s时液滴分布较为相似，可以得出液滴群的波动随着时间具有周期性。

(a) t=2.499 8 s(b) t=2.611 8 s

(c) t=2.771 8 s(d) t=2.803 8 s

图11 水平管x=3 150 mm截面内液滴群分布随时间的变化

图12为上弯头60°截面内液滴群的空间分布及随时间的变化，在上弯头内，离心力促使液滴群向弯头外侧运动，同样可以看出液滴群随时间波动的同时，整体分布形态又具有一定的相似性。

(a) t=2.499 8 s(b) t=2.611 8 s

(c) t=2.771 8 s(d) t=2.803 8 s

图12 上弯头60°截面内液滴群分布随时间的变化

图13为上弯头后的竖直管y=-290 mm截面内液滴群的空间分布及随时间的变化。结合y=-290 mm处的气相流线(图8(b))，可以看出液滴群主要集中在右侧(迎流侧)，在二次流作用下，液滴群由右侧沿着管壁逐渐向左侧运动，同时液滴群具有周期性的波动特性。通过前期的实验[11]可以发现，在该竖直管迎流侧存在液膜最厚值，与液滴群的分布具有很好的对应关系。

(a) t=2.499 8 s(b) t=2.611 8 s

(c) t=2.771 8 s(d) t=2.803 8 s

图13 竖直管y=-290 mm截面内液滴群分布随时间的变化

图14为下弯头60°截面内液滴群的空间分布及随时间的变化。在下弯头内，重力沿半径方向的分量与离心力方向相同，共同促使液滴群向弯头外侧运动。

(a) t=2.499 8 s(b) t=2.611 8 s

(c) t=2.771 8 s(d) t=2.803 8 s

图14 下弯头60°截面内液滴群分布随时间的变化

5 结 语

本文利用CFD软件，基于Euler-Eulerian两相流模型，对低含液输气管道内不同粒径分布的液滴群的空间分布以及随时间的变化规律进行了研究。运用边界层网格和增强壁面函数，能够获得近壁面处边界层内速度分布。上弯头后的竖直管内，沿流动方向，二次流中心由左侧逐渐向右侧移动。水平管内液滴群主要集中在管路底部区域，弯头内液滴群集中在弯头外侧，上弯头后的竖直管内，液滴群主要集中在迎流侧。液滴群分布随时间的变化具有周期性。