基于有限元的双轴差速系统实验台模态分析
杜付鑫,李 慧,冯显英,李沛刚,岳明君
(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室,济南 250061)
0 引 言
双轴差速式微量进给伺服系统是基于螺母驱动型滚珠丝杠的新型高精度微量进给系统[1-7],动态特性分析是提高进给系统稳定性和精度的基础。为了分析和控制滚珠丝杠进给系统,首先需要进行系统建模,包括电动机、联轴器、螺杆、螺母、工作台等。在该传动系统中,所有零件都是复杂的弹性系统。理论上,确定系统的振动形态需要获得系统中每个点的位移,但这通常是非常困难的。实际分析过程中,需要将连续系统进行离散,主要有两种建模方法:集中参数法和有限元法[8]。集中参数法是将进给系统中的质量元件用有限个质量块代替,系统中的弹性结构则用一些无质量的弹簧表示,结构阻尼用等效的阻尼元件表示。集中参数法建模较容易,而且可以体现传动系统低频段的动态特性,但集中参数法无法准确表征丝杠柔性体特征,并且其求解精度也不是很高。Guo-Hua等[9]使用集中参数模型分析了滚珠丝杠副预紧力与固有频率之间的关系。陈勇等[10]建立了滚珠丝杠副的接触振动模型,并研究了预紧载荷与接触振动之间的关系。
有限元法首先将系统离散成有限单元,该方法的计算速率与单元的大小及逼近模式的复杂程度关系密切[11-12]。Zaeh等[13]建立了考虑丝杠的弯曲变形的滚珠丝杠进给系统有限元模型。Okwudire等[14]基于Zaeh的工作,建立了考虑刚度矩阵中轴向、扭转及弯曲耦合项的进给系统有限元模型。Vicente等[15]研究了不同传动工况下的轴向与扭转分量来确定耦合度,并分析了不同载荷与不同螺母位置下的轴向振动模型与扭转振动模型的频率变化规律。
综上所述,有限元模型能够描述传动系统动力学细节特征,因此,本文采用有限元方法对双轴差速系统进行建模,并进行动态特性分析。
1 双轴差速驱动系统组成
图1所示为双轴差速式微量进给伺服系统,主要包括工作台、同步带、螺母轴电动机、丝杠轴电动机、螺母轴伺服驱动器、丝杠轴伺服驱动器、运动控制器、光栅尺等。

图1 双轴差速式微量进给伺服系统
2 基于有限元的双轴差速系统模态分析
2.1 进给系统结合部建模
2.1.1 固定结合部
对于双轴差速系统的固定结合部,忽略物理变形和螺栓分布等因素的影响,可近似认为接触压力在结合部上是均匀分布的。结合部单位面积的刚度可以通过计算固定结合部上的接触压力得到,结合部法向面压力p的计算公式如下:
式中:T为螺栓预紧力矩;l为螺距;μ1为螺旋副摩擦因数;r1为螺纹孔半径;β为导程角;μn为螺母支撑面摩擦因数;rn为螺母圆环面的当量摩擦半径;D1为螺母直径;D0为螺纹孔中径。应用吉村允孝法计算得到的刚度值如表1所示。
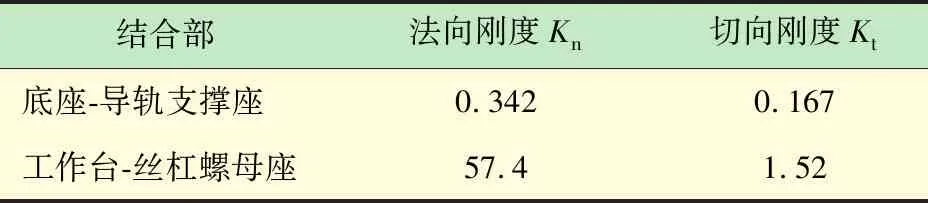
表1 固定结合部的刚度 GN/m
结合部建模时选用的刚度单元为MATRIX27,忽略阻尼的影响,将结合部刚度值用于模拟结合部的接触特性。如图2所示,固定结合部的2个接触面通过4个刚度单元并联连接,每个单元的法向刚度参数kn和切向刚度参数kτ为结合部的1/4。

图2 固定结合部动力学模型
2.1.2 滚动结合部
(1)螺母驱动型滚珠丝杠副结合部。螺母驱动型滚珠丝杠副区别于常规的滚珠丝杠副,采用螺母和螺母轴承一体化设计,本文所选型号为THK公司的DIR1605,一体化的螺母支撑轴承由两排接触角为45°的接触轴承背对背安装组成。通过查询手册,结合部接触刚度如表2所示。

表2 螺母驱动型滚珠丝杠副结合部接触刚度 GN/m
耦合丝杠和螺母的径向自由度,在丝杠和螺母之间沿轴向均匀布置4组轴向弹簧阻尼单元来模拟丝杠和螺母之间的轴向刚度,在螺母和螺母轴承之间均匀布置轴向和径向弹簧阻尼单元来模拟螺母轴承的刚度。螺母驱动型滚珠丝杠副结合部的等效动力学模型如图3所示。

图3 滚珠丝杠副结合部动力学模型
(2)滚动导轨副结合部。导轨结合部受力分析模型如图4所示。滚珠同滚道接触的压力角为β。F为法向载荷;FU和FL分别为上、下滚道中单一滚珠对滑块滚道和导轨滚道的法向作用力。

图4 滚动导轨结合部受力分析
建模方法如图5所示,导轨结合部的刚度值和阻尼值采用模态实验和仿真相结合的方法进行辨识,导轨结合部的辨识结果为342 MN/m。根据导轨和滑块之间滚珠的接触角度,在法向和切向分别均匀布置4个刚度单元。

图5 滚动导轨结合部动力学模型
(3)两端轴承结合部。双轴差速微量进给伺服系统采用一端固定,一端自由的安装方式,轴承的接触刚度参考THK样本手册,两端支撑轴承的刚度如表3所示。

表3 支撑轴承结合部刚度 MN/m
轴承结合部等效动力学模型如图6所示,丝杠固定端在丝杠和轴承接触处沿圆周均匀布置4个接触点,每个接触点用2个combin14弹簧阻尼单元分别表示1个轴向和1个径向刚度,丝杠自由端只在接触点处建立径向刚度单元。
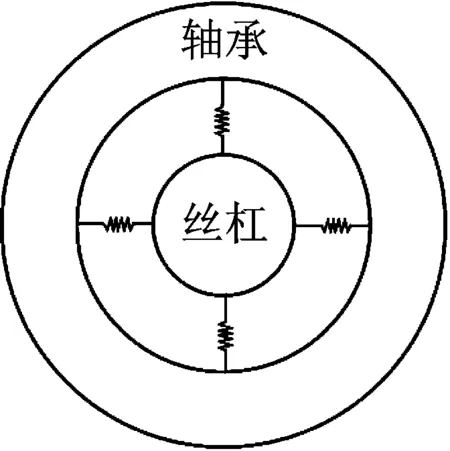

图6 轴承结合部动力学模型
2.2 进给系统理论模态分析
2.2.1 进给系统有限元建模
将在PRO/E中建立的三维模型导入到ANSYS中进行有限元建模。
(1)几何模型简化。忽略小螺栓孔以及其他工艺小孔;对倒角、倒圆均作直线化处理;忽略电动机和其他对计算结果影响较小的零部件。
(2)网格划分。如图7所示,首先选择Solid185作为整个模型的实体单元类型,然后在HyperMesh中进行网格划分,共划分了24 976个单元。
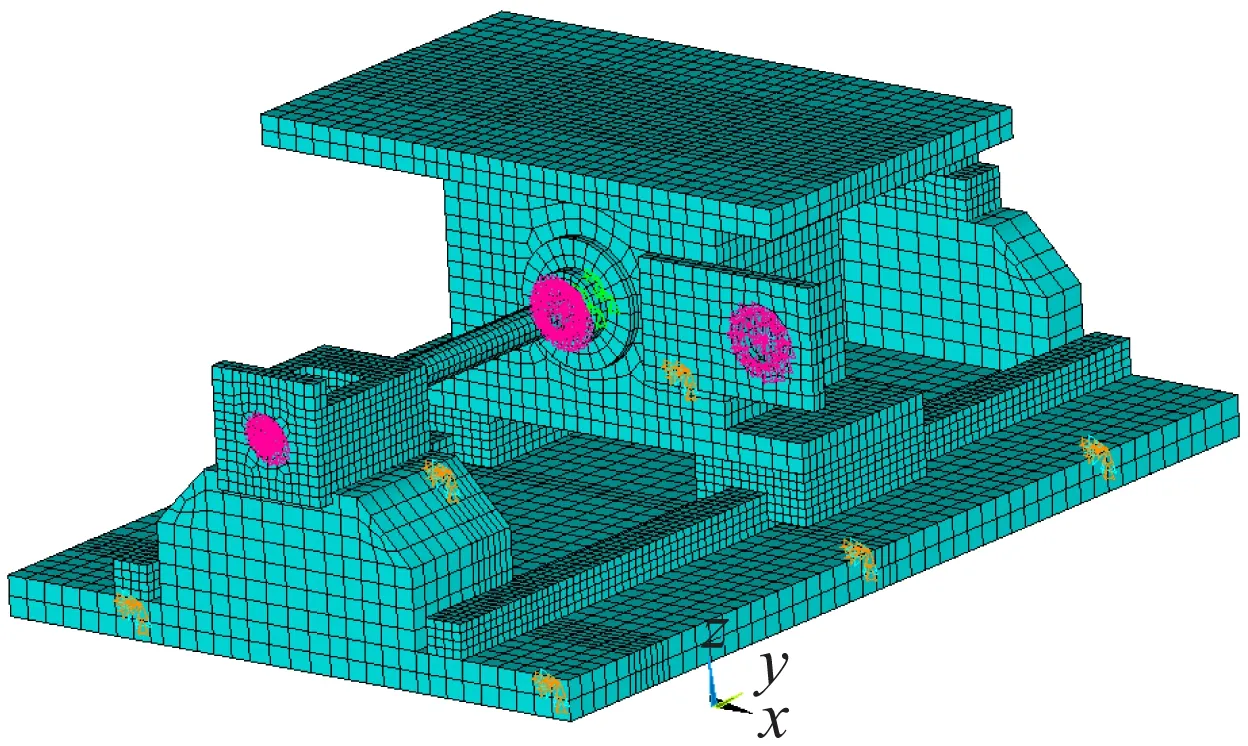
图7 网格划分结果
2.2.2 进给系统理论模态分析
前6阶固有频率和模态振型的有限元分析结果如表4和图8所示。

表4 理论固有频率和试验固有频率的对比
2.3 进给系统试验模态分析
模态测试试验如图9所示,试验仪器主要有BK8208型激振力锤、一个BK4525B型加速度传感器、NI公司PXIe-1075数据采集系统,ModalView模态分析软件。模态测试的结果见表4。由表4可知,第2阶理论固有频率误差为7.7%,其他各阶固有频率误差相对较小,均在5%左右,试验结果验证了理论模型的正确性。

(a)第1阶

(b)第2阶

(c)第3阶
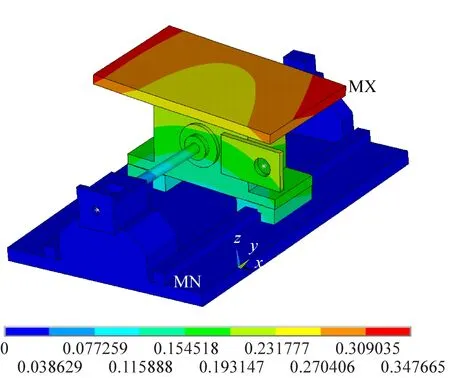
(d)第4阶

(e)第5阶
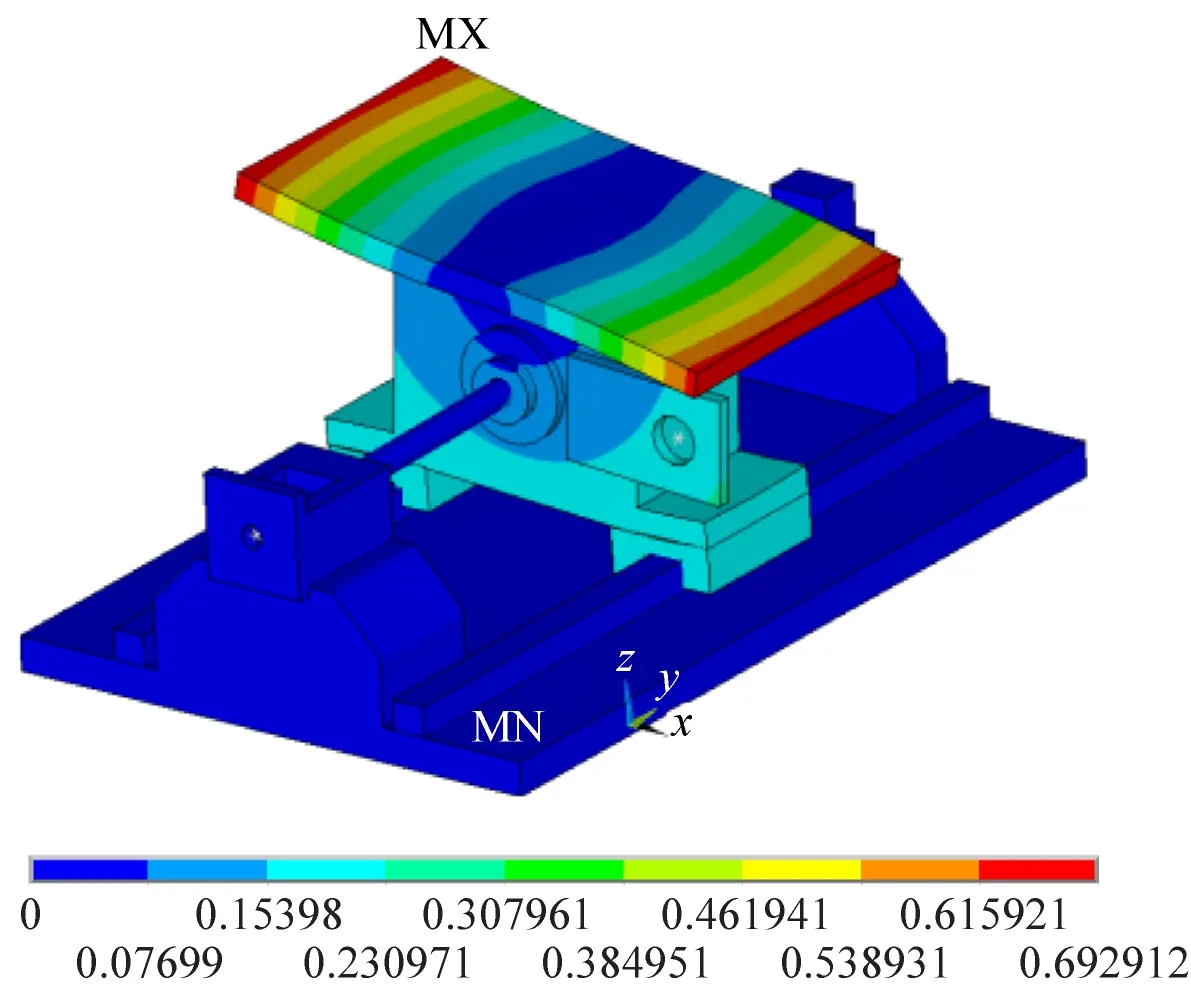
(f)第6阶
图8 前6阶理论模态振型
3 结 语
本文使用ANSYS建立了双轴差速微量进给伺服系统的有限元模型,对该系统进行了理论模态分析和模态试验,固有频率理论值误差的在8%以内,验证了结合部建模方法和有限元建模的正确性。模态分析为双轴差速微量进给伺服进给系统的结构设计和动态性能优化提供了理论依据。

