基于类脑模块化神经网络的污水处理过程关键出水参数软测量

蒙西 乔俊飞 韩红桂

城市污水处理过程是一个复杂的、大滞后的生物化学反应过程,具有多样性、随机性、不确定性、强耦合性、高度非线性、大时变等特征,其关键水质参数的检测和控制是污水处理厂稳定、高效运行的重要前提[1−3].目前,水质参数的检测方法可以分为三种[4−5]:人工取样化验法、在线仪表检测法以及软测量技术.其中,人工化验法操作繁琐,从取样到化验耗时较长,所需时间从几分钟到几天不等,例如对出水生化需氧量(Biochemical oxygen demand,BOD)的化验需要5天.人工化验的时滞会严重影响污水处理效果,易造成二次污染.与人工取样化验法相比,在线检测仪表能缩短检测时间,避免人工操作带来的偶然误差,但购买与维护成本却十分昂贵,大多数污水厂都无力配置足够规模的在线仪表.软测量技术通过机理分析建模来估计待测变量,由于污水过程极其复杂多变,现有的机理模型难以完全体现污水处理过程的特性,测量精度无法得到保证.因此,建立快速、精准、可靠的污水处理系统模型对出水参数进行软测量,是污水处理过程控制领域亟待解决的问题,具有重要的研究价值.

针对上述问题,基于数据驱动的智能化软测量方法在污水处理过程出水水质参数检测领域受到广泛关注和应用[6−9].由于人工神经网络的知识习得能力和非线性逼近能力在诸多非线性系统建模问题上已得到很好验证[10−13],许多学者开始将其应用于污水处理过程建模领域.Ráduly等[14]选用典型的前馈神经网络对出水BOD和出水化学需氧量(Chemical oxygen demand,COD)进行软测量,但测量精度有待提高.Bagheri等[15]通过多次对比实验验证了多层感知器和径向基函数(Radial basis function,RBF)神经网络在出水总悬浮物浓度(Total suspended solid,TSS)、出水总磷(Total phosphorus,TP)、出水COD以及出水氨氮(Ammonia nitrogen,NH4-N)软测量上的可行性,然而通过试凑法确定的网络结构和学习参数却无法保证建模效率和模型性能.文献[16]基于互信息设计了一种弹性径向基函数神经网络,实现了对出水BOD和出水COD的软测量,但算法中较多的参数会影响软测量模型在实际工业过程中的应用.结合神经网络与模糊推理系统,Wan等[17]分别建立了出水固体悬浮物浓度(Suspended solid,SS)和出水COD的软测量模型,该模型的泛化性能却有待提高.Li等[18]构建了一种用于解决非线性系统建模问题的自组织级联神经网络,当选用该网络对出水BOD和出水TP进行软测量时,获得了较理想的建模精度,但其网络结构却过于庞大.Han等[19]用一种改进的粒子群算法对RBF神经网络结构和网络参数进行同步优化,构建了基于自组织RBF神经网络的出水TP软测量模型,粒子群算法的引入却增加了时间复杂度,实际应用中会降低建模效率.综上分析,对于污水处理过程的多类出水参数(出水BOD、出水COD、出水TSS、出水NH4-N和出水TP等),目前大多数软测量方法都只是基于神经网络针对单一水质参数建模,所选用神经网络的性能决定了软测量模型的效率和精度.若神经网络信息处理能力不足,则无法保障模型的精度;若网络结构过大,则会增加模型复杂度、影响建模效率.此外,网络中较多的参数也会影响软测量模型在实际污水处理过程中的稳定性和应用推广.

针对上述问题,以不易获取的关键参数出水BOD和出水TP为目标,文中提出了一种基于类脑模块化神经网络(Brain-like modular neural network,BLMNN)的软测量方法.人脑在信息处理方面有着突出的优点,如学习、感知以及在复杂环境中做出决策等,都是现有机器学习系统所无法比拟且一直试图实现的[20].大脑的结构连接决定了其功能特性.模块化分区结构是大脑皮层的一大特征,人脑在学习、处理任务时,不同的分区处理不同的信息,具有“分而治之”特性[21].模拟人脑皮层结构和功能特性,基于BLMNN的软测量方法旨在通过“分而治之”实现对出水BOD和出水TP的实时、准确检测.首先基于互信息理论和专家知识,分析各参数变量与待测变量间的相关性,获取出水参数的辅助变量,有效降低了模型的复杂度.然后,针对各出水参数,采用改进的误差补偿(Improved error correction,IErrCor)[22]算法设计RBF神经网络来构建相应的子模型.IErrCor RBF神经网络能根据待处理任务自适应调整网络结构和参数,且结构增长和网络参数调整相互作用,在保证结构精简的同时提高了网络性能.因而采用IErrCor RBF神经网络构建的子模型具有理想的建模速度和模型精度.此外,文中还对子网络的收敛性和模型的计算复杂度进行了分析,从理论上体现了BLMNN模型的可靠性.最后,基于污水厂实际数据的仿真实验验证了所提出方法的有效性和优良性.因此,文中建立的类脑模块化神经网络软测量模型能有效应用于污水处理过程中,对实现污水处理过程的实时优化控制具有重要意义.

1 问题描述

1.1 特征分析

为保证污水处理厂持续、稳定、高效运行,对污水处理过程中的出水水质参数进行实时观测及评估至关重要.评估污水处理效果的出水参数众多,其中BOD是反映水质的最重要参数之一,能有效表示污水中有机物的含量.目前,出水BOD的浓度多通过人工化验获取,需要5天才能得到结果,远滞后于污水排放过程,无法用于对污水处理过程的实时闭环控制,易造成二次污染.此外,水体富营养化也是亟待解决的水环境问题之一,而磷元素是引起水体富营养化的主要因素,因此对出水TP的检测监控也十分必要.钼酸铵分光光度分析法和基于分光光度法的总磷在线分析仪测量是获取出水TP浓度的两种主要方法,其中化验分析法操作较为繁琐耗时,而在线仪表的购买与维护成本较高,多数污水厂无法配置足够数量的在线检测仪.因此,文中旨在实现对关键水质参数出水BOD和出水TP的实时、快速和精准检测.

1.2 建模策略

为了实现对关键出水参数BOD和TP的实时、高效测量,文中提出基于BLMNN的软测量建模策略,如图1所示.首先,对从污水处理厂获取的原始数据进行预处理,得到待处理任务样本集;然后,基于互信息分析和专家知识对样本集进行任务分解,选取与出水BOD和出水TP相关的辅助变量;确定子任务后,利用IErrCor RBF神经网络建立软测量子模型;最后,对子模型的结果进行整合,得到出水BOD和出水TP的实时检测值.

图1 BLMNN软测量模型策略图Fig.1 Strategy diagram of BLMNN soft-measurement model

1.3 类脑模块化神经网络(BLMNN)架构

图2 类脑模块化神经网络结构图Fig.2 Structure of brain-like modular neural network

类脑模块化神经网络(BLMNN)是一种模拟大脑皮层分区模块化结构、由多个子网络组成的神经网络,每个子网络承担全局任务的一个子任务,旨在通过“分而治之”来提高神经网络处理复杂任务的整体性能.文中选用BLMNN建立污水处理过程出水BOD和出水TP的软测量模型,其结构如图2所示.

图2中,D表示经预处理后的样本集,由待测变量Y和候选参数变量X组成;I(xi;y1)和I(xi;y2)分别为第i个变量与出水BOD和出水TP 间的互信息(i=1,2,···,21);D1和D2表示任务分解后的样本子集,和分别为子网络的输入,y1和y2表示采样得到的出水BOD和出水TP实际值,为子网络的输出;表示第h个子网络到第j个输出神经元的权系数(h=1,2;j=1,2);和表示BLMNN软测量模型得到的出水BOD和出水TP测量值.

1)任务分解

任务分解是实现“分而治之”的前提,文中通过任务分解选取各待测变量的辅助变量.由于影响出水水质的变量参数众多,若所有变量均作为辅助变量参与建模,则会增加模型的复杂度.另一方面,输入维数过高也会影响神经网络的非线性映射能力.因而在建模时有必要删除相关性低的变量,选取与待测变量相关性较高的变量作为辅助变量.目前,常用的辅助变量选取方法是基于多元统计相关性分析的主成分(Principle component analysis,PCA)分析法[23],通过将高维的变量数据投影至低维子空间来获取辅助变量.PCA分析法只能度量变量间的线性关系,忽略了变量间的非线性关系,具有一定的局限性.因此,文中基于互信息和专家知识分析变量间的相关性,将待处理任务D分解成两个独立的子任务D1和D2.首先,对于所获取的参数变量基于互信息分析其他变量与待测变量间的非线性关系,筛选出于与待测变量相关性较大的参数变量;然后,基于专家知识替换掉不易检测的变量,确定最终辅助变量.

2)子网络构建

子网络的性能是整个BLMNN模型性能的保障.构建子网络的核心思想是通过已知数据样本寻找待测变量与辅助变量间的非线性关系.实际工业应用中,建模精度和建模速度是受到重点关注的两大优化目标[24],而所设计的神经网络的类型、结构以及参数调整算法都会影响到最终的建模精度和建模速度.因此,有必要根据待解决的任务设计、构建合适的神经网络模型.针对每个子集D1和D2,文中采用IErrCor RBF神经网络寻找(Xh,Y h)间的非线性关系(h=1,2),构建软测量子模型,实时检测出水BOD和出水TP.

3)输出整合

输出层对子网络的输出进行处理,文中选用加权平均法对各子网络的结果进行整合,得到出水BOD和出水TP两个独立的输出.BLMNN的输出整合方法是基于任务分解的特点,由于出水参数的软测量被分解成两个独立的子任务,因此当其中一个子网络作用于某个输出时,另一子网络对该输出影响较小.

2 基于BLMNN的关键出水参数软测量模型

2.1 辅助变量选取

污水处理过程复杂多变,呈现出高度的非线性特征.经典的线性相关性分析方法难以有效探索提取出参数变量间的相关性,因此引入互信息对参数变量间的相关性进行度量,其最大的优势在于能有效刻画出参数间的非线性关系.

互信息能表示两个变量间共同拥有信息的含量,衡量变量间的相互依赖程度.给定两个随机变量X和Y,假定其边缘概率分布和联合概率分布分别为p(x),p(y)和p(x,y),则两变量间的互信息I(X;Y)可计算如下:

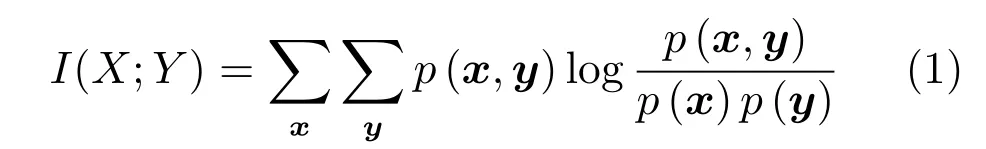
其中,边缘概率分布和联合概率分布基于直方图得到.当变量X和变量Y完全无关时,则互信息为0;反之,两者的相关性越大则互信息的值越大,所包含的相同信息也就越多.

基于获取到的北京某污水厂(活性污泥处理工艺)2014年的数据,对其进行预处理后按每天一组进行采样,得到365组数据,其中每组中的数据为各变量同一时间段获取的值,所包含的参数变量如表1所示.

对获取到的数据,通过式(1)分别计算其他参数变量与待测变量出水BOD和出水TP间的互信息值,选取与出水BOD和出水TP互信息值较大的6个变量作为辅助变量,如表2所示.在对出水BOD进行测量时,考虑到获取进水BOD测量值时间较长,因此用曝气池的污泥沉降比(Settling velocity,SV)替代进水BOD,其中SV与出水BOD间的相关性为0.2492.

表1 软测量模型候选变量Table 1 Candidate variables of the soft-measurement model

表2 软测量模型变量相关性分析Table 2 Correlation analysis between variables

2.2 基于IErrCor RBF 神经网络的子模型设计

由于RBF神经网络结构简单且具有良好的非线性映射能力,文中用该网络来构建子模型.对输入样本x,由RBF网络处理可得估计输出如下:

其中,wj为第j个隐层神经元到输出层的连接权值,φj为径向基函数:

则可在满足精度条件的前提下尽可能选择小的网络结构;若对网络精度要求较高,则可以适当增大网络结构获取期望的精度.以下对IErrCor RBF神经网络的设计算法进行详细介绍.

2.2.1 网络结构增长

初始时刻,隐含层中没有神经元.当第一个训练样本进入网络后,将该样本作为第一个隐含层神经元:输入向量作为神经元的中心,输出值作为隐含层神经元到输出神经元的连接权值,径向作用范围设为常数1:

t时刻,对所有训练集样本,计算当前误差向量:

其中,P是训练样本集的大小;第p个样本的误差分量由以下公式计算得到:

其中,ydp和分别为第p个样本的期望输出和t时刻的实际输出.

寻找当前误差峰值点所在位置:

第l个样本所对应的实际输出与期望输出误差最大,可以认为当前网络对第l个样本的学习能力不足.因此需要新增一个RBF神经元对当前样本进行学习,来补偿当前最大误差.新增神经元中心向量和输出权值设置如下所示:

与其他神经元不同,RBF神经元模拟了生物神经元局部响应特性,其宽度参数代表了神经元的径向作用范围.若宽度值太小,神经元的作用范围会较小;若宽度太大,相邻两个神经元易产生相同的作用,造成网络结构上的冗余.因此,宽度参数的设置至关重要.每新增一个神经元后,计算该神经元与已有神经元的欧氏距离并寻找最小距离:

选取该最小距离的二分之一作为新增神经元的初始宽度值,既保证了神经元的作用范围又能避免结构上的冗余:

2.2.2 网络参数调整

每增加一个神经元并完成初始参数设置后,采用一种改进的二阶梯度算法[25]对所有网络参数进行调整,调整规则如下:

其中,∆为需要调整的全部参数(中心向量、宽度、输出权值);Q为类海森矩阵;gt为梯度向量;I为单位矩阵;µ为学习率参数.

为了减小雅克比矩阵计算过程中的空间复杂度和时间复杂度,将类海森矩阵转化为多个类海森子矩阵的和:

其中,qp表示类海森子矩阵,jp为雅克比向量.

类似地,将梯度向量的计算也转化为P个梯度子向量的和:

其中,ηp表示梯度子向量.因此,对类海森矩阵和梯度向量的计算转化为对雅克比向量的计算:

根据链式求导法则,可得雅克比向量中的每个分量如下:

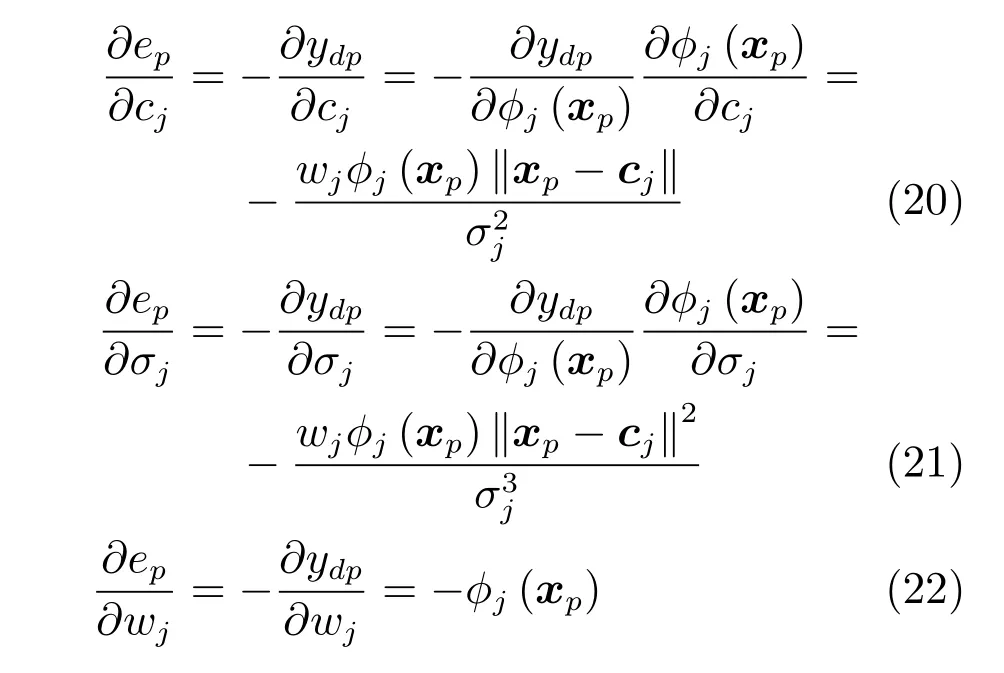
当达到预设最大结构或期望训练精度时,IErrCor RBF神经网络构建完成.文中选用均方根误差(Root mean square error,RMSE)的值来衡量网络精度,t时刻网络的RMSE值的计算如下:

2.2.3 网络收敛性证明和分析

为保证BLMNN软测量模型在污水处理过程中的稳定应用,下面给出子网络收敛性的证明和分析.

文中用于参数调整的二阶梯度算法是对经典牛顿法的一种改进.因而可以基于经典牛顿法对该算法进行收敛性分析.牛顿法迭代公式如下所示:

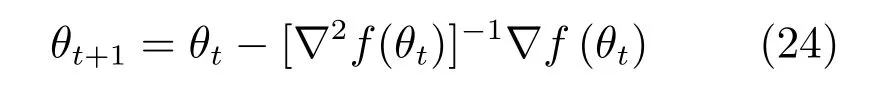
其中,θ为需要调整的参数,∇2f(θ)为海森矩阵,∇f(θ)表示梯度向量.

对于牛顿算法,可得到如下收敛定理:

定理1.设f(x)为二次连续可微函数,S为一个凸集,若对S上的点存在以下情况:

1)存在 “最优” 参数θ∗∈S,∇f(θ∗)=0.

2)∇2f(x)非奇异.

则该算法收敛于θ∗且收敛值位于初始值θ1附近.

证明.根据式(24),可得以下关系:

又因∇f(θ∗)=0,则可得:

由矩阵不等式特性可得:

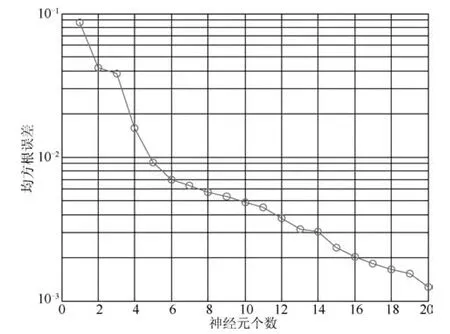
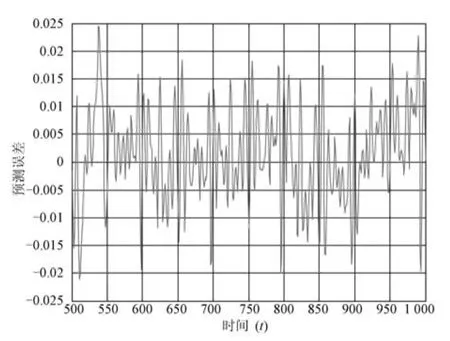
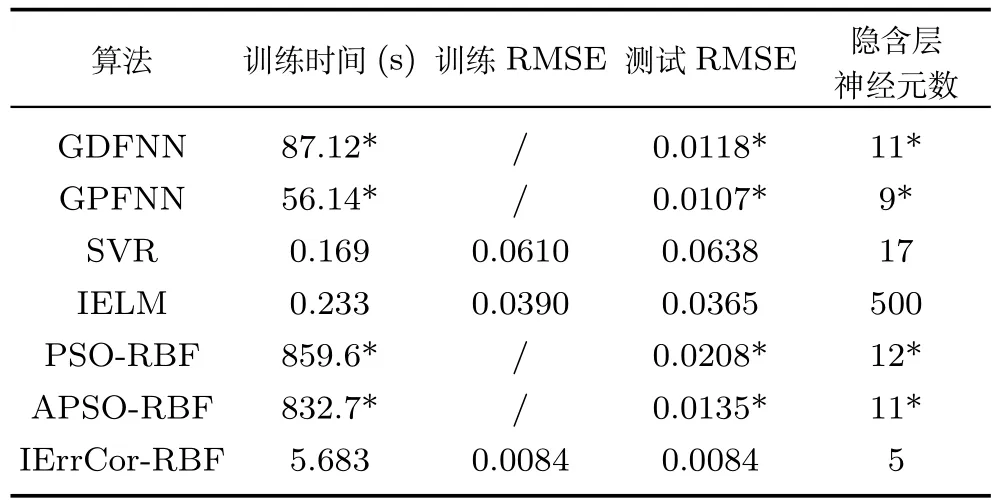
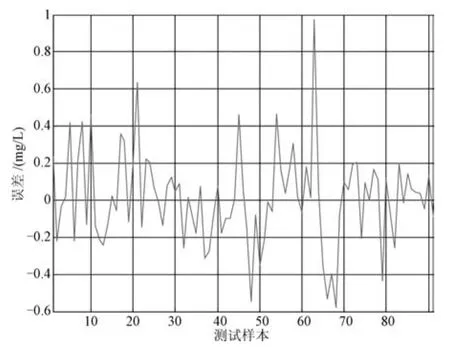
由于k[∇2f(x)]−1[∇2f(x)− ∇2f(y)]k≤k,0

因此,可认为存在0<∂t<1,使得:

由此可得:

其中,0<∂m<1,m=1,2,···,t且θ1为初始参数设置值.

当t→∞时,∂1∂2···∂t→0, 所 以limt→∞ θt=θ∗,算法收敛于θ∗. 同理可证θ∗位于初始值θ1附近.

由以上分析可知,当采用二阶梯度算法调整网络参数时,初始参数的设置会影响网络的收敛速度和最终收敛位置,因而较优的初始值能提高收敛速度和收敛性能.由于文中IErrCor RBF神经网络中的初始参数无随机值,都是基于待解决任务而设定的较优值,所以一定程度上保证了算法的收敛性和稳定性.

2.3 输出整合

当采用IErrCor RBF神经网络处理所分配的子任务后,输出层对各子网络的输出进行加权整合:

在BLMNN设计中,输出整合的方法与任务分解方法的特点相关联.该建模策略中,待处理任务被分解成两个独立的子任务,且子任务间互不影响.因此在整合时,当一个子网络作用于某个输出神经元,另一子网络对该输出影响较小可忽略不计.加权系数设置如下:

2.4 模型计算复杂度分析

为了更好描述BLMNN软测量模型在实际污水处理过程中的建模效率,对BLMNN计算复杂度进行分析.假设两个子网络的结构分别为M1-J1-1和M2-J2-1(M1或M2个输入层神经元,J1或J2个隐含层神经元,1个输出层神经元),计算可得BLMNN时间复杂度为:

其中,n1和n2代表子网络的迭代步数,P为训练样本个数.由式(32)可得,对于BLMNN软测量模型,当训练样本数一定时,若算法迭代步数越少、隐含层神经元数越少,则所构建的网络时间复杂度越低,建模效率越高.若选用经典的多输出RBF神经网络(网络结构为M-J3-2)进行建模,则时间复杂度为:

其中,n3表示RBF神经网络迭代步数.对比BLMNN和多输出RBF神经网络的时间复杂度,可得以下关系:

由于传统的RBF神经网络多需要通过试凑法确定网络结构且网络结构较大,而文中的子网络IErrCor RBF网络结构精简且能根据待解决任务自组织确定网络结构,因此n1J1

3 仿真实验与结果分析

文中仿真实验分为两部分:首先,通过基准实验(Mackey-Glass时间序列预测)验证子网络—IErrCor RBF网络的性能;然后,采用从污水厂获取的实际数据对BLMNN模型进行工业实验,通过与其他算法的对比体现了文中所提出软测量方法的有效性与优良性.

3.1 Mackey-Glass时间序列预测

该实验中,Mackey-Glass时间序列由以下离散表达式产生:

其中,n=10,a=0.2,b=−0.1,τ=17,x(0)=1.2;根据已有的{x(t),x(t−∆t),···,x(t−(n1−1)∆t)}来预测x(t+R)的值,且R=∆t=6,n1=4.预测模型如下所示:

利用龙格库塔法生成1000组数据,前500组数据作为训练样本,后500组作为测试样本.

结构增长与参数调整相互作用是IErrCor RBF神经网络的一大特性,从图3可以看出,随着结构的增加,网络的训练误差逐渐减小,当神经元数达到5时,均方根误差RMSE的值降低到0.01以下.接下来用包含5个隐含层神经元的IErrCor RBF网络去预测该时间序列,图4给出网络测试输出与期望输出的对比图,图5给出测试误差曲线,结果表明该网络在Mackey-Glass时间序列预测问题上能取得较好的预测效果.

另外,为了进一步对子网络性能进行评估,将 IErrCor算法与其他算法 — GDFNN[26]、GPFNN[27]、SVR[28]、IELM[29]、PSO-RBF[30]以及APSO-RBF[19]进行了对比,具体结果如表3所示.从对比结果可以看出,该算法在网络结构和预测精度上较其他算法都有明显优势,表明IErrCor RBF神经网络能以精简的结构取得较好的预测效果.虽然SVR和IELM 算法在训练时间上优于IErrCor算法,但IELM和SVR中算法参数较多,需要花费额外的时间去寻找最优设定值.与GDFNN、GPFNN、PSO-RBF以及APSO-RBF相比,IErrCor算法的训练时间则缩短了十倍甚至百倍.综上,IErrCor RBF在解决Mackey-Glass时间序列预测问题时有一定的优势,该实验很好验证了构建BLMNN模型的子网络性能.

图3 IErrCor RBF网络学习能力与结构的关系Fig.3 Relationship between the learning ability and structure of IErrCor RBF network

图4 IErrCor RBF网络实际输出与期望输出对比Fig.4 Prediction results of IErrCor RBF network

图5 IErrCor RBF网络预测误差曲线Fig.5 Prediction errors of IErrCor RBF network

表3 Mackey-Glass时间序列预测结果对比Table 3 Performance comparison of different algorithms on Mackey-Glass prediction

3.2 污水处理出水BOD和出水TP软测量

文中基于北京某污水处理厂(活性污泥处理工艺)2014年的实际过程数据进行工业试验,对其进行预处理后按每天一组进行采样,得到365组数据,将其分为三组:183组作为训练样本;91组作为验证样本;91组作为测试样本.选用训练时间和测试时间评价模型效率、隐含层神经元数评价模型结构、均方根误差(RMSE)和平均百分比误差(Absolute percentage error,APE)评价模型精度,其中RMSE值可由式(23)得到,APE值计算方式如下:

图6为基于BLMNN建立出水BOD软测量子模型时,训练误差、验证误差以及测试误差随子网络结构增长的变化图.随着隐含层RBF神经元数量的增加,网络的训练误差会逐渐降低,但增加到一定程度则会出现过拟合现象.从图6中可以看出,当神经元数量增加到11后,网络的验证误差和测试误差不再降低反而增加.因而在神经网络实际应用过程中,为避免出现过拟合现象,有必要引入交叉验证过程.文中选取出现过拟合前的网络结构(10个隐含层神经元)进行建模.用91组测试样本对建立好的BOD软测量子模型性能进行测试,图7和图8分别为测试输出和测试误差,可以看出基于所设计模型得到的出水BOD测量值能较好逼近实际采样值.

图9为基于BLMNN建立出水TP软测量子模型时,训练误差、验证误差以及测试误差随网络结构增长的变化情况.选用包含5个神经元的IErrCor RBF神经网络进行建模,模型的测试结果和测试误差曲线在图10和图11中给出,从图中可以看出软测量模型的出水TP检测值能较好逼近实际采样值.

图6 出水BOD软测量子模型性能与结构间的关系Fig.6 Relationship between structure and performance of the effluent BOD soft-measurement sub-model

图7 BLMNN模型出水BOD软测量测试结果Fig.7 Testing results of BLMNN soft-measurement model on the effluent BOD

图8 BLMNN模型出水BOD软测量测试误差Fig.8 Testing errors of BLMNN soft-measurement model on the effluent BOD

图9 出水TP软测量子模型性能与结构间的关系Fig.9 Relationship between structure and performance of the effluent TP soft-measurement sub-model

图10 BLMNN模型出水TP软测量测试结果Fig.10 Testing results of BLMNN soft-measurement model on the effluent TP

图11 BLMNN模型出水TP软测量测试误差Fig.11 Testing errors of BLMNN soft-measurement model on the effluent TP

为了进一步验证BLMNN软测量建模方法的优越性,将该方法与另外6种方法(RBF、GAP-RBF[31]、IELM、SVR、APSO-RBF、SCNN)进行了对比研究,其中“RBF”为经典的多输出RBF神经网络,其辅助变量为除去两个待测变量外的21个参数变量;不同建模方法的测量结果如图12(a)∼(l)所示,从图12与图11的对比中可以看出,相较于其他方法,基于文中模型得到的出水BOD和出水TP估计值能更好地拟合实际值的变化趋势,具有较高的建模精度.

图12 不同算法对出水TP和出水BOD软测量测试结果Fig.12 Testing results of different soft-measurement models on the effluent TP and effluent BOD

另外,为了定量对比分析不同方法的建模性能,表4给出各方法重复实验20次的统计结果.当选用多输出RBF神经网络建立出水BOD和出水TP软测量模型时,隐含层平均需要106个神经元,而选用BLMNN建立模型时,两个子网络共需15个RBF神经元.对比模型效率和模型精度,BLMNN也较多输出RBF神经网络有了显著提高,体现了“分而治之”的优势.从模型训练时间对比中可以看到,GAP-RBF,IELM,SVR和SCNN方法在建模效率上要优于BLMNN,但GAP-RBF无法获得理想的模型精度,而IELM模型结构则过于庞大.虽然SVR方法在测量出水BOD时能取得较为理想的结果,但在测量出水TP时精度较低.APSO-RBF模型结构要优于大部分方法,但粒子群算法的引入却牺牲了建模效率.相较于其他方法,BLMNN软测量模型具有精简的结构、理想的建模效率以及较高的精度.当用建立的BLMNN软测量模型对出水BOD和出水TP进行检测时,能以0.0013秒和0.0008秒得到测量结果,表明所提出的方法能实现对关键出水参数的实时检测.此外,BLMNN模型中无随机参数或需要人为提前设定的参数,有利于该算法在实际工业过程中推广应用.综合以上分析,BLMNN能根据待处理任务建立合适的模型,实现对污水处理过程关键出水参数的实时以及高精度检测.

表4 不同算法对出水BOD和出水TP软测量统计结果对比Table 4 Testing results of different soft measurement models on the effluent TP and effluent BOD

4 结论

针对城市污水处理过程中关键出水参数难以实时、准确检测的问题,文中提出了一种基于BLMNN的软测量建模方法,模拟人脑“分而治之”处理复杂任务的特性,实现了对出水BOD和出水TP的同步、实时、准确检测.该建模方法具有以下特点:

1)模拟大脑皮层的分区特性,实现了对关键水质参数出水BOD和出水TP的同步、实时测量.

2)基于互信息和专家知识选取相关辅助变量,降低了模型的复杂度,提高了子模型的性能.

3)IErrCor RBF神经网络结构精简、收敛较快、且具有良好的非线性映射能力,用该网络构建的子模型有效地保证了整个BLMNN软测量模型的效率和精度.

4)不同于其他算法需要提前寻求最优参数,BLMNN模型中的初始参数基于待处理任务的样本数据设定.通过初始参数对网络收敛性能影响的理论证明,体现了该算法在实际应用中的可靠性.对BLMNN计算复杂度的分析也表明文中提出的软测量模型具有较好的建模效率.

目前,基于BLMNN的污水处理过程出水参数软测量方法的研究尚处于探索阶段,模型的结构和性能都还有改进和提升空间.从仿真实验验证结果可以看出,该模型在关键水质参数出水BOD和出水TP的测量问题上具有显著优势,期望在下一步的工作中能实现对更多出水参数的有效测量.