一种二阶内反馈控制器SO-IFC的研究与应用
李军 万文军 刘哲
高志强[1]将控制科学划分为3个范式:“工业范式、模型范式和抗扰范式”.模型范式代表了现代控制论的思维方式和世界观[1],基础在于系统的建模与辨识包括优化,将系统的数学模型作为研究问题的出发点.经过数十年的发展,产生了宏大和严密的现代控制论和众多先进的控制策略[2−10],其中模型预测控制(Model predictive control,MPC)[3−6]被认为是目前现代控制论在过程控制中应用最成功的控制方法[10],例如在石油化工控制工程得到成功应用[5−6];从MPC的适用范围看,文献[11]指出:“从应用对象来看,主要还限于线性或准线性过程”.由于石油化工工业的产品可以中间存储,其过程特性可近似为确定的线性或准线性过程.
现代控制论的发展一直受到源于实际应用困难的质疑.文献[12]指出:“近年来控制理论研究受到来自应用的严峻挑战,其表现形式为理论研究与应用之间的鸿沟有扩大的趋势”.文献[1]指出了控制科学研究中的娱乐数学现象.简单说就是理论研究成果一大堆,真正有用的却寥寥无几,这就是理论与实际的鸿沟,鸿沟无非是人们长期寻求全面超越PID(Proportional-integral-derivative)[13−15]控制的愿望落空.现代控制论的理论成果虽然完善和严密,但在客观上它丝毫没有撼动经典PID[13−15]控制技术在工业过程控制的主导地位,文献[1]指出:“原因也许是真正的控制问题不是建模–优化问题”.
简单地认识现代控制论:将控制问题转换为数学问题确定化,并且在确定性问题的研究上取得了良好的进展和突破,例如丰富的理论论证与仿真验证成果包括成功的工程应用实例;但是在控制实际中,还存在大量的不确定性问题,例如对象模型的不确定性、过程的时变性、过程的非线性、不确性扰动等问题.对于这些不确定性问题要如何解决?现代控制论并没有给出实质性的答案,这可能就是先进控制论存在的固有的缺陷之一.目前看,抑制不确定性问题的最有效方法仍然是包括PID在内的闭环控制或者反馈校正[16−17],闭环控制对于先进控制依然很重要.在没有找到或者没有应用比PID控制性能更好的闭环控制方法之前,在不确定性问题的抑制上,先进控制与PID控制不会有太大的区别.也许根本没有“鸿沟”,真正起到负面作用的是“固有的缺陷”包括“看不见的缺陷”.
值得关注的是,韩京清[18]提出了不依赖模型的自抗扰控制技术(Active disturbance rejection control,ADRC)从理论上解决了不确定性抑制的问题.ADRC是一种以扩张状态观测器(Extended state observation,ESO)[19]为核心的新型控制技术.在阶次已知包括不存在纯滞后问题的前提下,如果ESO的带宽趋于无穷大,则ADRC能够实现零误差跟踪扰动,这就是文献[1,20]指出的带宽与误差的反比关系.但是在控制实际中,准确阶次同样难以获取.另一方面,即便知道准确阶次,但是对于高阶对象,高阶ADRC不一定具有工程意义[21].
在控制实际中,如果实际对象的特性接近二阶系统也包括一阶系统的特性,包括二阶惯性特性[22]、二阶振荡特性[23]、双积分特性[24]、二阶非线性特性[25]、二阶时变特性[26]等,则采用二阶控制器能够实现比较好的控制性能,包括比较好的扰动抑制性能等.二阶控制器具体包括PID 控制器[13−15]、二阶线性ADRC控制器(Linear active disturbance rejection controller,LADRC)[27]等.
长期以来,围绕改进PID控制性能的各种研究也一直没有间断.文献[28−30]提出将先进控制与PID控制相融合,例如基于改进遗传算法的PID参数整定[28]、基于神经网络的PID参数整定[29]、基于改进粒子群算法的PID参数整定[30]等.他们采用的是一种“建模–优化”的策略,为了取得最优的控制效果,通常需要辨识出控制回路的精确模型.
实践经验表明,如果是低阶对象,采用PID控制已经足够了.将包括PID控制在内的低阶控制器用于大滞后对象的跨阶控制才是真正的控制难度所在.所谓大滞后是高阶较大惯性和较大纯滞后特性的一种简称.作者认为:跨阶控制难度的根源在于“低阶控制器并不真正适合于直接用于大滞后过程的跨阶控制”,例如文献[28−30]提出的“建模−优化”策略并不能从根本上改善包括PID在内低阶控制器在大滞后过程的跨阶控制性能,存在“看不见的缺陷”.原因很简单,无论你如何对PID控制参数进行整定和优化,但它在大滞后过程的跨阶控制性能始终不如文献[21]提出的一种内反馈控制方法(Internal feedback control,IFC).
滤波方法的性能也是决定控制系统性能的一个重要性因素,例如滤波相位和时间的滞后造成控制回路稳定裕度下降.韩京清[18]指出:“PID的主要问题之一是没有合适的微分信号提取装置”,影响了PID性能的发挥.将问题扩大来看,首先是没有好的滤波方法.在控制实践中,微分器对噪声干扰的滤波特性往往是微分器运用中首要考虑的因素.韩京清[18]从非线性最速跟踪(Nonlinear optimal tracking,NOT)[31]的角度提出了非线性跟踪微分器 (Nonlinear tracking differentiator,NTD)[31−33],NTD显著提高了输出跟踪输入微分的“效率”.但是NOT和NTD也存在明显的不足,例如NOT跟踪输入和NTD跟踪输入微分的特性还与输入的幅值有关;文献[34−35]从新型正弦跟踪(New sinusoid tracking,NST)的角度分别提出了一种新型正弦跟踪滤波器(New sinusoid tracking filter,NSTF)[34]和一种新型正弦跟踪微分器(New sinusoid tracking differentiator,NSTD)[35].显著特点是:NSTF跟踪输入和NSTD跟踪输入微分的“效率”较高或滞后较小,噪声滤波特性较好,输出特性与输入幅值无关等.
文献[21]提出了一种基于并联降阶(Parallel reduction order,PRO)和高增益PI(High gain of PI,HGPI)控制器的内反馈控制方法IFC,将HGPI的实际控制的阶次降低为一阶,有效提高了低阶控制器用于大滞后过程的跨阶控制性能.IFC的显著特点还在于运用了新型正弦跟踪滤波器NSTF[34],较好保证了IFC的控制性能;实际运用的结果表明,将IFC运用于大滞后过程控制,具有良好的鲁棒性能和良好的扰动抑制性能等,是目前能够找到的一种综合特性相对比较好的而且实用的一种过程控制策略.目前IFC已经在大型火力发电机组的一些重要的过程控制系统,例如机组的协调控制系统、锅炉的再热汽温控制系统、机组的脱硝控制系统等取得了良好的实际运用效果.
文献[21]提出的IFC也是一种一阶内反馈控制器(First order of IFC,FO-IFC).为了进一步提升IFC的控制性能,文中提出了一种基于高增益PID(High gain of PID,HGPID)控制器的二阶内反馈控制器(Second order of IFC,SO-IFC).SO-IFC在闭环响应速度和扰动抑制性能上均优于FO-IFC.
由于SO-IFC参数的整定依赖准确的对象模型,例如并联降阶PRO依赖准确的阶次,阶次本身也是一种重要的模型参数.针对在控制实际中准确模型和准确阶次难以获取的问题,文中提出了一种不依赖准确模型和准确阶次的工程参数整定方法(Engineering parameter tuning method,EPTM),显著特点在于避开了模型辨识[36]和模型降阶[37]类似PID参数整定[28−30]等繁琐的问题.
文中变量包括符号的表达具有唯一性,可相互引用.
1 二阶内反馈控制系统
在论述二阶内反馈控制器SO-IFC之前,首先需要对内反馈控制器IFC[21]和新型正弦跟踪滤波器NSTF[34]有一些了解.
1.1 内反馈控制器
文献[21]提出的内反馈控制系统(Internal feedback control system,IFCS),如图1所示.

图1 内反馈控制系统结构示意图Fig.1 Structure diagram of internal feedback control system
在图1中,输入函数发生器(Input function generator,IFG)用于简单的过程轨迹控制,内反馈器(Internal feedback device,IFD)用于过程对象(Process object,PO)的并联降阶,将高增益PI控制器HGPI的实际控制的阶次降低为一阶.新型正弦跟踪滤波器NSTF用于控制回路噪声干扰的滤波.
在图1中的“内扰”和“外扰”主要是指信号上的扰动.另外,对象模型的不确定也是一种内扰.外扰通过扰动模型(Disturbance model,DM)直接叠加在过程对象PO的过程输出中,相当于一种耦合作用.
1.2 新型正弦跟踪滤波器
对滤波方法的研究始终是控制理论研究中的一个重要的问题.在控制实践中,二阶惯性滤波器(Second order inertial filter,SOIF)[34]在过程信号的滤波或去噪[38]方面有广泛的应用.但是SOIF输出跟踪输入的“效率”较低或滞后较大.
SOIF可变形为一种LC滤波器[34]和LCR正弦跟踪器(LCR Sinusoid tracking,LCR-ST)[34]的变形结构[34].在SOIF变形结构的基础上,如果采用新型正弦跟踪器(New sinusoid tracking,NST)[34]取代LCR-ST,则构造出新型正弦跟踪滤波器,即NSTF.相对SOIF,NSTF输出跟踪输入的“效率”较高或滞后较小.
LCR正弦跟踪器LCR-ST是一种LCR带通滤波器[39],新型正弦跟踪器NST的基础是一种正交混频方法[40].
SOIF变形结构传递函数,表达为

式中,WSOIF(s)为SOIF的传递函数.TSOIF为惯性常数,单位s.WLC(s)为LC滤波器传递函数.WLCR-ST(s)为LCR-ST的传递函数.TSOIF也代表NSTF的滤波时间常数.
对式(5)给出的过程对象PO在单位阶跃激励的过程输出分别进行SOIF和NSTF滤波,用YPO(t)表达PO单位阶跃激励输入的过程输出.其中在n=4,Tα=100s,Kα=1,TSOIF=20s,得到的实验结果,如图2所示.
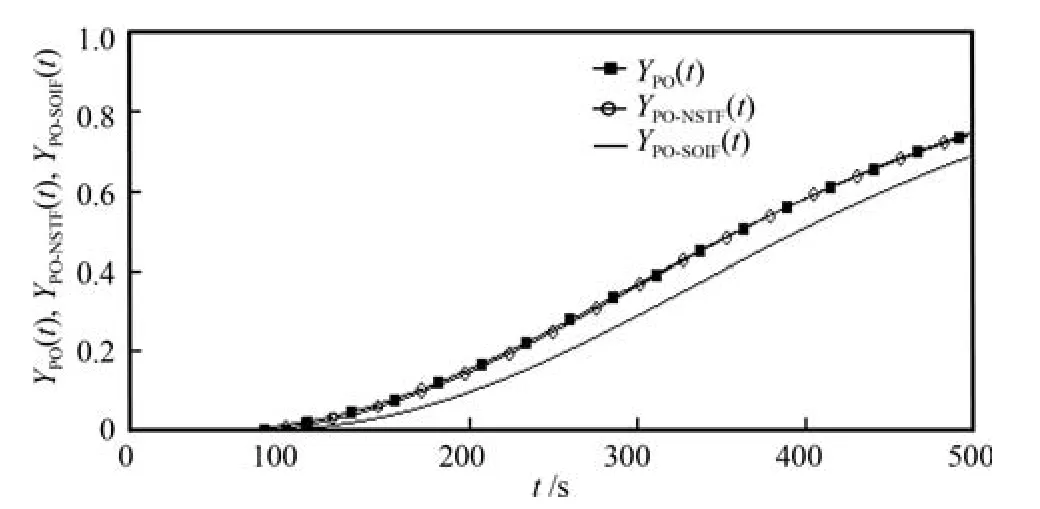
图2 滤波特性对比示意图Fig.2 Comparison of filter characteristics
在图2中,YPO-SOIF(t)为SOIF跟踪YPO(t)的输出,YPO-NSTF(t)为NSTF跟踪YPO(t)的输出.可见,NSTF跟踪YPO(t)的特性远优于SOIF.
NSTF的传递函数难以具体表达,这是事物的矛盾性所决定的,但由于NSTF输出跟踪输入的滞后较小,从工程计算的角度考虑,完全可以忽略NSTF.
更多NSTF的内容可参考文献[34].
1.3 二阶内反馈控制器
文中提出的二阶内反馈控制系统(Second order of internal feedback control system,SO-IFCS),如图3所示.

图3 二阶内反馈控制系统结构示意图Fig.3 Structure diagram of second order of internal feedback control system
由图3可知,二阶内反馈控制器SO-IFC由高增益PID控制器HGPID和新型内反馈器(New internal feedback device,NIFD)所构成.由于HGPID的高频增益极高,因此采用了两级NSTF滤波.
NIFD传递函数为

式中,WNIFD(s)为NIFD的传递函数.KNIFD为NIFD的增益,无量纲.TNIFD为统一的时间常数,单位s.n为整数阶次,无量纲.
HGPID传递函数为

式中,WHGPID(s)为HGPID的传递函数.KHGPID为HGPID的增益,无量纲.HGPID内含理想微分器TNIFDs.
理想微分在物理上不可实现[35],如果单独对理想微分器TNIFDs的输出进行NSTF滤波,则得到新型正弦跟踪微分器NSTD[35].
将HGPID看成是NIFD的一种逆向变换器,即SO-IFC是NIFD的逆模型.则得到SO-IFC传递函数,为

式中,WSO-IFC(s)为 SO-IFC 的传递函数.WSO-IFC(s)分子的s项阶次大于分母s项阶次2阶,因此SO-IFC的高频增益极高,需要在SO-IFC外部设置两级NSTF滤波.
另外,可以证明,在HGPID与NIFD构成的闭环系统中,SO-IFC是高度稳定的.
不考虑NSTF,则SO-IFCS闭环传递函数为
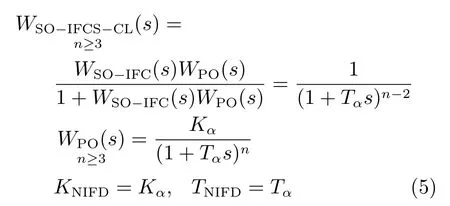
式中,WSO-IFCS-CL(s)为 SO-IFCS的传递函数.WPO(s)为PO的传递函数.Tα为PO的惯性常数,s.Kα为PO的增益,无量纲.
由式(5)可知,在PO模型已知的情况下,则WSO-IFCS-CL(s)相对PO传递函数WPO(s)的阶次n降低了2阶,表明了SO-IFCS具有很高的闭环响应速度.
如果从降低HGPID控制阶次的角度看问题,则NIFD是PO的并联降阶器.NIFD与PO并联传递函数为

式中,WNIFD+PO(s)为NIFD与PO并联后的传递函数.
由式(6)可知,如果PO模型已知,则NIFD与PO并联的结果得到二阶惯性环节,也就是将HGPID控制的阶次降低为二阶.
1.4 参数整定
如果PO模型已知,则SO-IFC参数整定相对简单,基本原则如下:
设置NIFD与PO的阶次n相同;
设置KNIFD=Kα;
设置TNIFD=Tα;
式(4)要求KHGPID趋于无穷大,如果在数字计算机中实现HGPID,KHGPID不能趋于无穷大,则HGPID参数设置原则为:KHGPID>>1/KNIFD.但同时满足:KHGPID 两级NSTF起到一种噪声干扰的滤波包括理想微分的降阶作用,TSOIF越大,滤波效果也越好.在工程应用上,TSOIF的合适范围在0.05∼0.3Tα之间. 不考虑NSTF,则SO-IFCS开环频域函数,为 式中,WSO-IFCS-OL(jω)为SO-IFCS的开环系统频域函数.WPO(jω)为PO 的频域函数.WNIFD(jω)为NIFD 的频域函数.GSO-IFCS-OL(ω)为SO-IFCS的开环系统频域增益,无量纲.θSO-IFCS-OL(ω)为 SO-IFCS的开环系统频域相位,单位◦.PMSO-IFCS-OL为SO-IFCS的开环系统频域相位稳定裕度,单位◦. 具体在PO和SO-IFC阶次n=4,Tα变化范围1∼300s,Kα变化范围0.5∼1.5.设置TNIFD=100s,KNIFD=1,KHGPID=90.得到PMSO-IFCS-OL的计算结果,如图4所示. 由图4可见,在给出PO的Tα和Kα的变化范围,PMSO-IFCS-OL的稳定的范围较宽. 在控制实际中,过程增益(Process gain,PG)和过程总滞后(Process all lag,PAL)特性相对容易得到,例如通过在现场的开环阶跃激励响应实验获取PG和PAL,如图5所示. 在图5中,PR(t)为过程比值,具体为开环阶跃激励响应的过程值与输入阶跃激励幅值的比值,无量纲.PRend为PR(t)的终值.Tτ为纯滞后,单位s.T0.63为PR(t)上升到0.63PRend的时间,单位s.Tend为趋势段的截止时间,单位s.PRend代表了PG,T0.63则代表了PAL. 图4 SO-IFCS开环系统频域相位稳定裕度Fig.4 Schematic diagram of frequency domain phase stability margin of open loop system of second order of internal feedback control system 图5 开环阶跃激励响应实验示意图Fig.5 The trend of step response experiments of open loop 对于工程参数整定方法EPTM 来说,无需知道准确的对象模型包括准确的阶次和准确的纯滞后等.在Tτ/T0.63<0.5时,利用PRend和T0.63进行SO-IFC工程参数整定已经足够了. 通过在现场的开环阶跃激励响应实验获取PRend和T0.63,然后凭工程经验给出一个相对高的整数工程阶次neng,则得到工程参数为 根据neng,得到NIFD传递函数为 出于工程参数计算的需要,定义一个工程对象(Engineering object,EO),暂且指定EO为三阶惯性加纯滞后对象,为 式中,WEO(s)为工程对象EO的传递函数,暂且指定EO的纯滞后为3Tα. 其中,在Kα=1,Tα=100s,在EO 输入为1,测得T0.63≈619s.出于对比,分别取neng=6、8、12,则得到SO-IFC工程参数,如表1所示. 表1 SO-IFC工程参数Table 1 Engineering parameter of second order of internal feedback controller 其中,在KHGPID=90,Kα=1,Tα变化范围1∼250s,得到SO-IFCS开环频域相位稳定裕度PMSO-IFCS-OL的计算结果,如图6所示. 图6 工程参数整定方法的开环系统频域相位稳定裕度(图1)Fig.6 Schematic diagram of frequency domain phase stability margin of open loop system of engineering parameter tuning method(Fig.1) 由图6可见,neng越大,PMSO-IFCS-OL随Tα变化的特性也越平坦,表明了通过提高neng能够获得更好的鲁棒性能. 在工程应用上,不一定需要设置过高的KHGPID,其中在neng=8时,分别设置KHGPID=0.5、2、100,得到PMSO-IFCS-OL的计算结果,如图7所示. 由图7可见,通过降低KHGPID,能够获得更好的鲁棒性.计算结果表明,在KHGPID>2时,KHGPID变化对PMSO-IFCS-OL的影响已经不明显了. 仿真实验的数值计算由数字计算机完成,文中无特别说明,数值离散计算间隔为1s.SO-IFC的输入和外扰采用阶跃信号.仿真实验主要从抑制不确定性的方面考察SO-IFC的性能. 其中IFG采用二阶惯性环节,为 式中,WIFG(s)为IFG的传递函数,TIFG为IFG的惯性常数,单位s. 图7 工程参数整定方法的开环系统频域相位稳定裕度(图2)Fig.7 Schematic diagram of frequency domain phase stability margin of open loop system of engineering parameter tuning method(Fig.2) 出于仿真实验的需要,扰动模型DM采用一阶惯性环节,用TDM表达DM的惯性时间常数,单位s. 文中同时给出了SO-IFC与PID控制的实验对比结果.PID中的微分作用采用实际微分器环节[41].用PVSO-IFC(t)表达SO-IFC控制的过程输出信号,用COSO-IFC(t)表达SO-IFC控制器的输出信号.用PVPID(t)表达PID控制的过程输出信号,用COPID(t)表达PID控制器的输出信号. 对PID参数整定的原则是:在输入阶跃给定时,过程输出超调量不超过5%. 在PO参数为:n=4,Kα=1,Tα=100s.得到NIFD参数为:n=4,TNIFD=100s,KNIFD=1.设置KHGPID=90,TIFG=100s,TSOIF=15s,TDM=100s.其中在输入为1,外扰为0.5,得到的实验结果,如图8所示. 在图8实验结果基础上,在PO中增加80s纯滞后,得到的仿真实验结果,如图9所示. 在图8实验结果基础上,对PVSO-IFC(t)和PVPID(t)进行平方处理,即 [PVSO-IFC(t)]2和[PVPID(t)]2,目的是模拟高阶非线性对象.其中在输入为1.5,外扰为0.25,得到的实验结果,如图10所示. 由图8∼10可见,相对PID控制,SO-IFC在外扰抑制性能上包括在抑制对象的不确定性和非线性的性能上具有良好的优势. 在图8实验基础上.在PVSO-IFC(t)中加入相对幅值为0.01的白噪声干扰.其中在输入为0,外扰为0,得到的实验结果,如图11所示. 图8 二阶内反馈器控制特性仿真实验结果(图1)Fig.8 The diagram of control characteristic simulation results of second order of internal feedback controller(Fig.1) 图9 二阶内反馈器控制特性仿真实验结果(图2)Fig.9 The diagram of control characteristic simulation results of second order of internal feedback controller(Fig.2) 由图11可见,NSTF对白噪声干扰具有显著的抑制作用.在不使用NSTF滤波的前提下,则SO-IFC的控制输出被白噪声严重干扰. 根据第1.6节给出的工程对象EO,其中在Kα=1,Tα=100s,在EO 输入为1,测得T0.63≈619s.按neng=8整定SO-IFC的工程参数.得到TNIFD≈77s,KNIFD=1,TIFG=77s.设置KHGPID=90,TSOIF=15s,TDM=100s.其中在输入为1,外扰为0.5,得到的实验结果,如图12所示. 图10 二阶内反馈器控制特性仿真实验结果(图3)Fig.10 The diagram of control characteristic simulation results of second order of internal feedback controller(Fig.3) 图11 二阶内反馈器控制特性仿真实验结果(图4)Fig.11 The diagram of control characteristic simulation results of second order of internal feedback controller(Fig.4) 由图12可见,相对PID控制,采用工程参数整定的SO-IFC对高阶纯滞后工程对象具有较好的控制特性.实验结果验证了EPTM的有效性. 将文中SO-IFC运用于某电厂的某1000MW超超临界燃煤机组的锅炉主控系统的优化.锅炉主控系统包括汽机主控系统是机组协调控制系统的基本组成部分.协调控制系统有二种控制模式,分别为“炉跟机”和“机跟炉”控制模式.其中在“炉跟机”控制模式下,汽机主控系统控制机组负荷,锅炉主控系统控制锅炉主汽压力,主要优点是机组负荷跟踪给定负荷的动态特性较好,但锅炉主汽压力跟踪锅炉压力给定的动态偏差较大.所述锅炉主控系统和汽机主控系统均采用常规的PID控制策略. 将SO-IFC用于所述锅炉主控系统的优化,优化的主要目的是改善“炉跟机”控制模式下,锅炉主汽压力跟踪锅炉压力给定的动态特性. 采用SO-IFC优化,如图13所示. 图12 工程对象控制特性仿真实验结果Fig.12 The diagram of control characteristic simulation results of engineering object 图13 锅炉主控系统优化示意图Fig.13 The optimization diagram of boiler master control system 在采用SO-IFC优化过程,出于对比,保留了原PID控制策略,并且考虑了SO-IFC与PID之间的无扰切换问题. 其中在机组负荷725MW,通过现场实验得到该锅炉主控输出-锅炉主汽压力对象的等效二阶模型(Equivalent second order model,ESOM)为 式中,WESOM(s)为ESOM的传递函数.但ESOM并不代表实际对象的模型一定是二阶的,其中还包含有纯滞后的因数等. ESOM 对应的T0.63≈562s,按neng=8整定SO-IFC的工程参数.得到TNIFD≈70s,KNIFD=0.92.实际设置KHGPID=3,TIFG=70s,TSOIF=20s.因KHGPID较低,实际采用了一级NSTF滤波的结构. 在采用SO-IFC优化后,得到所述锅炉主控系统的控制特性,如图14(a)所示. 将锅炉主控由SO-IFC控制切换到常规PID控制,找一段与图14(a)接近的变化趋势进行比较,包括锅炉主控输出、锅炉压力给定、锅炉主汽压力趋势的高低限和趋势的时间长度相同等,如图14(b)所示. 图14 控制特性对比示意图Fig.14 Comparison of control characteristics 由图14(a)可见,在采用SO-IFC优化后,锅炉主控输出变化比较平稳,能有效克服外界扰动.在稳态负荷条件下,锅炉主汽压力跟踪锅炉压力给定(2小时内)的最大误差为0.28MPa.在变负荷条件下,锅炉主汽压力跟踪锅炉压力给定的最大动态误差为0.68MPa. 由图14(b)可见,在切换到常规PID控制后,锅炉主控输出的波动较大.在稳态负荷条件下,锅炉主汽压力跟踪锅炉压力给定(2小时内)的最大误差为0.51MPa.变负荷条件下,锅炉主汽压力跟踪锅炉压力给定的最大动态误差为1.17MPa. 通过图14的对比可知,相对PID控制,所述锅炉主控系统采用SO-IFC优化后,在稳态负荷条件下,锅炉主汽压力跟踪锅炉压力给定(2小时内)的最大误差从0.51MPa降低为0.28MPa.在变负荷条件下,锅炉主汽压力跟踪锅炉压力给定的最大动态误差为从1.17MPa降低为0.68MPa.可见,采用SO-IFC优化收到了明显的效果. 另外,长期投运的结果表明,运用SO-IFC控制对煤种的变化具有良好的适应性. 采用高增益PID控制器HGPID,将新型内反馈器NIFD用于高阶对象的并联降阶,将HGPID控制的阶次降低为二阶,将新型正弦跟踪滤波器NSTF用于HGPID的降阶处理或噪声干扰滤波,构造出具有良好鲁棒性和扰动抑制性能的二阶内反馈控制器SO-IFC.工程参数整定方法EPTM在较大程度简化了SO-IFC参数的整定.采用降低控制阶次的方法,是提高低阶控制器在大滞后过程跨阶控制性能的有效途径.SO-IFC的主要缺点在于高增益PID控制器HGPID的高频增益极高,需要采用两级NSTF滤波的结构,增加了SO-IFC的复杂程度.在实际运用中,完全可根据需要设置HGPID的实际增益,如设置较低的增益也是可能的.在HGPID的增益较低时,可采用一级NSTF滤波的结构;文中提出的方法是对控制理论的有益发展,具有重要的理论研究和工程应用价值.数学分析,仿真实验和实际电力工程应用的结果,验证了文中所提出观点和方法的正确性和有效性.1.5 鲁棒性能分析

1.6 工程参数整定方法



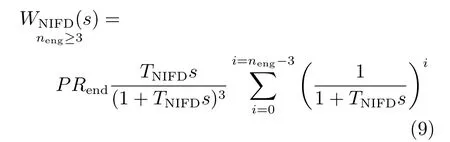



2 仿真实验






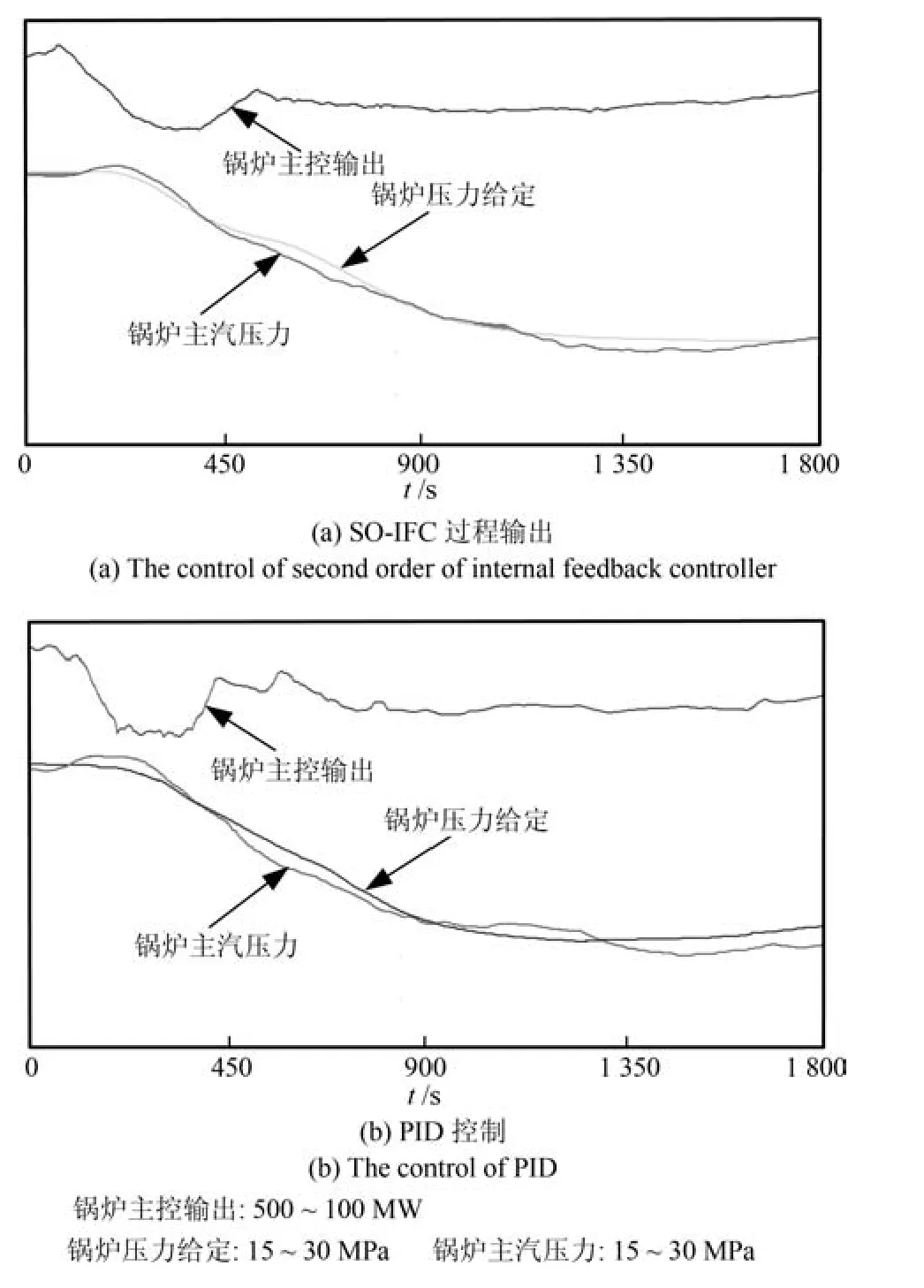
3 实际应用



4 结论

