基于边介数模型的差分隐私保护方案

黄海平，王凯，汤雄，张东军

（1. 南京邮电大学计算机学院，江苏 南京 210023；2. 江苏省无线传感网高技术研究重点实验室，江苏 南京 210023）

1 引言

快速发展的社交网络应用促使大量社交数据被广泛使用，对用户隐私构成了威胁[1]。因此，社交网络的研究者通过在节点参数和图结构中添加噪声来实现数据隐私保护。然而，即使是引入噪声的图数据仍然可以实现去匿名化，尤其是在攻击者具备相应网络背景知识的前提下。随着社交网络在全球范围内的普及，攻击者将更容易获得各种类型的背景知识，隐私泄露的风险也随之增加。

为了加强隐私保护的效果，差分隐私技术[2]被应用于社交网络中。最早的差分隐私只是对社交网络数据进行一些简单的统计分析，大多只涉及属性信息而忽略了结构信息，许多重要的图属性都可以通过子图计数查询得到。其后，关系差分隐私框架出现，它保证了社交网络中任何一条边的改变都不会对查询结果造成太大的影响。然而，尽管关系差分隐私框架将需要引入的噪声量从网络中节点数量的多项式级别减少到了多项式对数级别，但相对于查询函数中节点的数目，关系差分隐私需要引入的噪声量依然是超指数级别的，查询结果的数据可用性依然很难保证。为了在不泄露隐私的情况下安全地发布真实的社交网络图数据，可应用一个更加强健的匿名技术框架[3]，其以精妙的方式修改图结构以提高隐私保护程度，而保留大部分的原始图结构。然而，这类方法通常仅能针对一种特定类型的攻击方式，而对一些新型的去匿名化攻击技术效果不佳。

鉴于此，本文将寻求一种提供图数据隐私保护且能保留图结构的方案，该方案将“重要性”相同的边划分成为单独的组进行加噪处理，在提供了较高强度的隐私保护性的同时，保证了社交网络图的数据可用性。本文的主要贡献如下。

1) 结合dK-匿名结构将排序后的2K序列根据条件进行聚类操作，划分成一组组子序列，使 2K序列敏感度上限显著减少，从而大大降低了所需引入的总噪声量。

2) 提出基于边介数模型的差分隐私保护方案BCPA（betweenness centrality protection algorithm），根据介数排序的dK序列将原始图中“重要性”相同或相近的边聚类在同一子序列中，分组加噪时能保证不改变各条边的“重要性”，在保留了更多结构特征的同时也具有更好的数据可用性。

3) 提出一种基于邻接度的隐私保护性衡量算法，可以有效地衡量扰动对原始图数据的影响程度。

2 相关工作

近年来，针对社交网络图结构的差分隐私，研究者们取得了很多成果。Hay等[4]提出k-边差分隐私，即2个邻图最多相差k条边，以求扰动程度与隐私保护强度之间的平衡，与常用的节点差分隐私相比，其减小了校准噪声的添加，使图结构分析在k-边差分隐私时较为准确。Mir等[5]试图用随机Kronecker图[6]生成与原始图具有相似敏感度的差分隐私拓扑图，提供较为准确的真实图像，同时保护其中参与个体的隐私。Day等[7]引入基于边加法的图投影方法，提出2种基于聚合和累加直方图的方法来发布满足差分隐私的扰动图，通过降低敏感度来生成逼近真实度分布的拓扑图。

在处理差分隐私发布图时，研究者广泛运用了dK图隐私模型。Sala等[8]提出一种dK图隐私模型，设计了dK-PA（dK-perturbation algorithm）处理差分隐私的图发布，使用dK图查询并获取图结构的dK序列，对查询结果dK注入差分隐私噪声获得扰动的dK序列。其后，Sala等[8]又设计出DRC（divide randomize and conquer）算法，通过对加噪之前的dK序列进行聚类分组，以降低算法复杂度，但是由于全局敏感度较大，所提出的 2K图隐私模型实用性比较低。Wang等[9]结合dK图模型与随机矩阵图模型，设计了针对图的1K、2K、3K模型处理算法注入扰动参数，获取网络图的边差分隐私。兰丽辉等[10]针对权重社交网络，结合dK图模型设计LWSPA（protection algorithm based on Laplace noise for weighted social network）对查询结果集中的三元组序列进行分割，再对每个子序列构建满足差分隐私的算法，将查询结果集映射为一个实数向量，通过在向量中注入 Laplace噪声实现隐私保护。然而，这些方法在数据可用性方面仍显不足，除非隐私参数ε被设置成不合理的大值。

通过对上述相关工作的研究与分析，本文提出了基于边介数模型的差分隐私处理方案。在该方案中，选用dK图模型来实现图的差分隐私。根据给定的原始网络图，生成对应的 2K序列；根据边中介中心性系数对2K序列进行重新排序；将排序后的序列聚类为一个个子序列，并分组进行扰动[11]以满足差分隐私；将扰动后的各子序列整合成完整的新2K序列，并还原成图进行发布。最后，本文将该隐私保护方案与已有经典方案进行比较，实验结果表明，在较高隐私需求的情况下，其隐私保护性和大部分数据可用性都具有一定优势。

3 模型与算法描述

3.1 差分隐私定义

差分隐私是由Dwork[2]提出的一种隐私保护模型。该模型可以保证即使攻击者获得了所能掌握的最大背景知识，仍无法识别某一条数据记录是否存在于该数据集中。同时，该模型还提出了一种量化分析方法来表示隐私保护强度。

定义1若给定 2个数据集D1和D2，有且只有一条记录不同，表示为，则称D1和D2为兄弟数据表。对于随机算法A，Range(A)用来表示该算法的输出结果集合，即对于D1与D2的算法输出结果S∈Range(A)，若满足式(1)，则称算法A满足ε-差分隐私。

其中，概率Pr表示隐私被披露的风险；ε为调节算法A隐私保护强度的参数，即隐私预算参数，ε越小，数据的安全性越高[12]。

定理1非交互输出扰动[13]。设有函数集F，其敏感度为S(F)，K为向F中每一个函数f的输出添加独立噪声的算法。若该噪声为参数值取的Laplace分布，则算法K满足ε-差分隐私。其中，对以兄弟数据表为输入的查询函数，敏感度S(F)为其查询结果的最大曼哈顿距离。

证明见文献[13]。

定理2组合性质[14]。假设有n个随机算法，其中Ai满足εi-差分隐私，且任意2个算法的操作数据集没有交集，则{Ai}(1≤i≤n)组合后的算法满足max(εi)-差分隐私。

证明见文献[14]。

由定理1可知，敏感度S(F)和差分隐私参数ε决定了实现差分隐私需要添加的Laplace噪声量。

3.2 dK序列及2K敏感度分析

dK序列是一组描述图属性的数据集合，它可以将不同细节级别的图结构表示为统计信息。随着d值的增加，描述的图属性也更加具体。

对于给定的图G，0K分布只是图的平均节点度；1K分布则是图的度数分布；2K分布是图的联合度分布，即具有不同节点度组合的2节点子图的数目；3K分布表示具有不同节点度组合的3节点子图的数目，即聚类系数分布。在极限情况下，nK分布（其中n是图中的节点数）可以捕获完整的图结构。图1给出一个详细的示例，其中列出了所给图的2K序列和3K序列。

图1 dK序列示例

dK模型是一个图构造模型，它利用dK序列捕获的结构性统计数据集合，生成与原始图结构类似的图。对于给定的图G，dK图模型可以对其进行分析以产生相应的dK序列，然后使用相应的生成器来构造使用dK序列作为输入的合成图。

本文方案主要运用2K图模型，因此2K序列敏感度在其中起到至关重要的作用。设图G=(V,E)，其中V是节点的集合，E是连接V中节点对的边的集合。2K序列形式上是元组{dx,dy;k}的集合，其中，每个元组表示具有度dx和dy且连接分量为 2的节点对的数量为k。设m为元组的总数目，dmax是图G中的最大节点度数，有，且在图G为完全图时取得最大值，因此

函数的敏感度被定义为当函数域中的一个元素被修改时，函数输出的最大曼哈顿距离。2K序列的域是图G，G的邻图是所有与G相差至多一条边的图G′。改变G中的一条边将导致在相应的2K序列中改变一个或多个条目。因此，2K序列的敏感度等于所有G的邻图G′中的2K序列的最大变化数。

定理 32K序列敏感度上限[8]。2K序列的敏感度S2K的上限为4dmax+1。

证明见文献[8]。

由定理1可知，对于给定的差分隐私参数ε，敏感度的上限决定实现差分隐私所必要的噪声添加量，因此在这里只讨论2K序列敏感度的上限。如果使用更高阶的dK序列，将造成更高的敏感度值，这必然会降低生成的合成图的精确度。

3.3 基于边介数模型的差分隐私处理方案

3.3.1 方案算法流程

若直接对图G的2K序列进行随机扰动以满足差分隐私，需引入大量的噪声。根据定理 3，任意图G上2K序列的敏感度S2K的上限为4dmax+1。为了显著减少实现给定级别差分隐私所必须添加的噪声量，本文方案根据各元组中边中介中心性系数的平均值大小对2K序列进行重新排序，将数据分割成一组组子序列，然后独立地对每个子序列进行扰动以实现ε-差分隐私。下面本文将证明如果在每个划分出的子序列上实现ε-差分隐私，在整个2K序列也将实现ε-差分隐私。具体算法流程如算法1所示。

算法1基于边中介中心性系数的分组差分隐私

输入由给定图G生成的2K序列，用{dx,dy;k}表示，子序列数量n

输出满足差分隐私的新2K序列，用{d′x,d′y;k′}表示

1) 求出2K序列的元组数量q；

2) fori= 1 toq

4) end for

6) 将排序后的2K序列聚类为一组组子序列；

7) fori= 1 ton

8) 利用dK扰动算法向子序列注入噪声；

9) end for

10) 将扰动的子序列合成为新的序列{d′x,d′y;k′}；

具体的实现过程将在3.3.2节～3.3.4节介绍。

3.3.2 边介数排序算法

边中介中心性系数（edge betweenness centrality）定义为网络中所有最短路径中经过该条边的路径的数目占最短路径总数的比例[15]，即网络中包含成员i的所有最短路径数占所有最短路径数的百分比。它表示边i的控制能力，其值越大就代表有越多的节点需要通过它才能与其他节点发生联系[16]。对于给定图G，N为其节点数目，i是图G中任意一条边，则边i的中介中心性系数的计算式为

其中，nst表示节点s与节点t之间最短路径的数目，而nst(i)表示节点s与节点t之间通过边i的最短路径的数目。

由3.2节可知，2K序列是元组{dx,dy;k}的集合，其中每个元组表示具有度dx和dy且连接分量为 2的节点对的数量为k，即度为dx的节点和度为dy的节点之间连接边的数量为k。对于每个元组，求出其中包含的边的中介中心性系数平均值，并根据中介中心性系数平均值由小到大对2K序列重新排序。具体算法流程如算法2所示。

算法2边中介中心性系数平均值计算

输入由给定图G生成的2K序列，用{dx,dy;k}表示

输出2K序列的边中介中心性系数平均值

1) 求出2K序列的元组数量q；

2) fori= 1 toq

3) 筛选出符合{dx,dy}度分布的k条边；

6) end for

7) 根据边中介中心性系数平均值由小到大对2K序列重新排序；

边中介中心性系数可以量化表示某一条边在图中的“重要性”，通过引入边中介中心性系数，对2K序列重新排序，将“重要性”相同或相近的边进行聚类分组，在扰动时能够有效地保留原始图的属性与结构特征，使加噪后的图数据具有较好的研究意义。

3.3.3 分组差分隐私噪音添加

将排序后的2K序列R根据数据集大小划分为n个子序列，第i个命名为Ri，i∈[1,n]。n的大小由数据集大小决定，若数据集较大，则选择相对较大的n；若数据集较小，则选择相对较小的n。依照下面2条规则对R序列进行聚类。

1) 每个子序列只能获取R序列中的连续元组。

2) 每个元组必须出现且仅可以出现在一个子序列中。

根据上述2条规则，可以获得连续且相互不相交的子序列Ri。由定理3可知，这2条规则对于子序列敏感度性质是非常重要的。

定理4子序列独立性。对于排序后的2K序列R，当i≠j时，R序列的任何子序列Ri与Rj的敏感度相互独立。

证明该定理是基于以下假设利用反证法进行证明的。假设Ri的敏感度受到发生在Rj中的变化的影响，i≠j。在不失一般性的前提下，假设i＜j，并且T(i′)是Ri中的元组，T(j′)是Rj中的元组。假设在节点v1和节点v2之间形成一条新边，其中节点v1的相应元组＜T(i),T(i+1),…＞∈Ri且节点v2的相应元组＜T(j),T(j+1),…＞∈Rj。由于此事件可能发生的最大变化次数受v1和v2的度值的限制。令d1为v1的新度值，Ri中变化的元组的最大数目为d1-1个被删除的元组和d1个添加的元组，即小于2d1。对称地，令d2为v2的新度数，因此Rj中变化的元组的最大数目小于2d2。即使d1和d2等于它们的子序列中的最大度值dmax，如在定理3中规定的，每个子序列中涉及的变化的数目是2dmax＜4dmax+1，这意味着Ri和Rj的敏感度不会相互影响，与该假设相矛盾。

证毕。

利用dK扰动算法，计算要注入2K序列的噪声以满足ε-差分隐私。dK扰动算法是基于 Laplace分布 Lap(λ)中的随机变量改变 2K序列的每个元组的噪音添加算法。

定义2设DK是对图G生成的2K序列执行差分隐私机制，使。对于至多相差一条边的任何图G和G′，如果满足式(3)，则DK满足ε-差分隐私。

其中，S2K为2K序列的Laplace机制敏感度，O为DK(G)可能的输出，μ为2K序列的元组个数。

根据定理3，若直接对2K序列R添加噪声，该噪声为参数取值的Laplace分布，且μ值为整个2K序列R的元组个数。若如算法2所述，先对 2K序列进行聚类分组，获得连续且相互不相交的子序列Ri，则每个子序列的敏感度为再运用定义 2对每个子序列Ri注入参数为的Laplace噪声，这将大幅减小扰动噪声的添加量，理由如下。

设di为相应子序列Ri中节点的最大度数，μi为相应子序列Ri的元组个数，则该噪声为参数且μi值为子序列Ri的元组个数。由于di≤dmax且μi≤μ，因此对噪声添加量的缩减是指数级别的，这意味着在获得相同隐私保护强度的情况下，聚类操作将很大程度上减小对原始图结构的扰动。

随后利用dK扰动算法向每个子序列注入噪声使每个子序列都满足ε-差分隐私，再将加噪后的子序列整合为一个新的2K序列。下面将证明如果在每个划分出的子序列上实现ε-差分隐私，在整合之后的2K序列上也将实现ε-差分隐私。

定理5子序列组合性质。给定n个满足ε-差分隐私的不同的Ri子序列，i∈[i,n]，它们合成的2K序列R也满足ε-差分隐私。

证明对于n个满足ε-差分隐私的子序列Ri。根据定理4，当i≠j时，任何子序列Ri与Rj的敏感度相互独立，即每个Ri引入噪声量相互独立。根据定理2，合成的2K序列R满足ε-差分隐私。

证毕。

3.3.4 2K随机图生成算法

给定无向图G=(V,E)，其节点数n=|V|，边数m=|E|。设deg(v)为节点v的度数，Vk为度数为k的节点集合。

联合度矩阵JDM定义为

此矩阵描述连接度为k的节点和度为l的节点之间的边的数量，2K序列可以容易地由联合度矩阵推导得出。根据同一个联合度矩阵，2K序列可以构造出不止一个在结构和属性上有略微差异的图。

2K随机图生成算法如算法3所示。

算法32K随机图生成

输入联合度矩阵JDM′

输出满足JDM = JDM′的随机图

1) 创建|V|个节点，每个节点拥有deg(v)个可用端口；

2) 对于所有(k,l)∈JDM′，令JDM (k,l) = 0；

3) for (k,l)∈JDM′(k,l)

4) while JDM (k,l)＜JDM′(k,l)

5) 任选不相连的 2个节点v∈Vk及w∈Vl；

6) ifv没有可用端口

7) 调用算法4 NeighborSwitch(v)；

8) end if

9) ifw没有可用端口

10) 调用算法4 NeighborSwitch(w)；

11) end if

12) JDM (k,l)++；JDM (l,k)++；

13) end while

14) end for

初始化过程中，创建|V|=n个节点，分别以它们的度数作为标号。对每个节点v∈V，根据它们各自的度数分配 deg(v)个可用端口。初始状态下全部节点都尚未连接，所以将JDM (k,l)中所有度数对(k,l)的值初始化为 0。随后算法开始进行迭代，在每次迭代中，选择2个不相连的节点v和w，度数分别为k和l。当JDM (k,l)没有构造完全时，将v的一个可用端口与w的一个可用端口连接起来以创建边(v,w)，并且将相应的2个项JDM (k,l)和JDM (l,k)的值增加1。直到当前JDM的所有条目已经达到其在JDM′(l,k)中的目标值，2K图构造完成。

2K随机图生成算法的核心在于：当JDM (deg(v),deg(w))尚未达到其目标值时，即使不相连的2个节点v和w中的任一个或两者都没有可用端口时，也总是可以在它们之间添加一条边。在添加边(v,w)之前，对于没有可用端口的每个节点，对边执行重新布线。这一操作被称为“邻节点转换”。

将没有可用端口的节点定义为饱和节点，将至少有一个可用端口的节点定义为不饱和节点。邻节点转换算法如下。

算法4邻节点转换算法（NeighborSwith）

输入饱和节点i

输出生成边(i′,j)

1) 选择不饱和节点i′；

2) if deg(i′) == deg(i)

3) 选择与i相连且与i′不相连的节点j；

4) 删除边(i,j)；

5) 添加边(i′,j)；

6) end if

对一个给定节点i进行邻节点转换，可以在不改变当前JDM的情况下为节点i释放一个可用端口。由于deg(i′) == deg(i)，邻接点转换保证了JDM(deg(v),deg(w))的值不会改变。

4 实验仿真与性能分析

本节主要通过仿真实验来分析本文方案 BCPA的隐私保护性和数据可用性，并将其与同样使用差分隐私机制的dK-PA方案和DRC方案进行比较。其中，dK-PA模型是直接对2K序列进行加噪处理，而另外2种模型都是基于2K序列排序聚类加噪算法。不同的是，DRC模型是基于节点度大小对 2K序列进行排序，而BCPA是基于边中介中心性系数进行重新排序。

为了验证本文方案是否适用于社交网络图结构，如表1所示，选取wiki-Vote和ego-Twitter这2个真实社交网络数据集作为测试数据集，它们分别是维基百科who-votes-on-whom网络数据和Twitter社交网络数据。这2个数据集都具有以下2个显著特征：1) 节点度的统计个数符合幂律分布；2) “小世界”的特征，更接近真实世界。

表1 测试数据集

4.1 隐私保护性评估

为了量化差分隐私保护算法对原始数据图的具体扰动，针对社交网络图结构的特点，本文基于dK模型设计了一种基于邻接度的隐私保护性衡量算法，具体如算法5所示。

算法5隐私保护性衡量算法

输入原始图G(V,E)，扰动图G′(V′,E′)

输出隐私保护性P

1) 计算原始图中的边个数m，计算扰动图中的边个数m′，Ddiff= 2mmax；

2) 对于节点u，u∈G，找出与u所连接的其他节点的度，降序排列并存储在link(u)=(d1,d2, ... ,dn)，其中n表示节点u的度；

3) 反复执行步骤2)和步骤3)，直至遍历所有节点；

4) 对于节点u′，u′∈G′，找出与u′所连接的其他节点的度，降序排列并存储在 link(u′)=(d1′,d2′, ... ,dn′′)，其中n′表示节点u′的度；

5) if id(u)==id(u′)

6) 找出 link(u)和 link(u′)相同的度关系，每找出一个，则Ddiff=Ddiff－1；

7) end if

8) 反复执行步骤5)～步骤8)，直至遍历所有节点；

9) 计算隐私保护性P；

分别生成原始图相邻节点度序列和扰动图相邻节点度序列，比较2个序列，得到2个序列之间不相同的值的个数Ddiff，取原始图的边数量m和扰动图的边数量m′。

2组数据中边数量的最大值为

隐私保护性为

隐私保护性P的取值范围为0～1，值越大，隐私保护程度越高。当隐私保护性P较小时，表示邻接节点的度改变较小，此时攻击者仍然有很大概率实施结构攻击和度攻击。

根据算法5，实验分别对BCPA、DRC和dK-PA这3种方案进行了仿真，以达到比较3种算法的隐私保护效果，如图2所示。

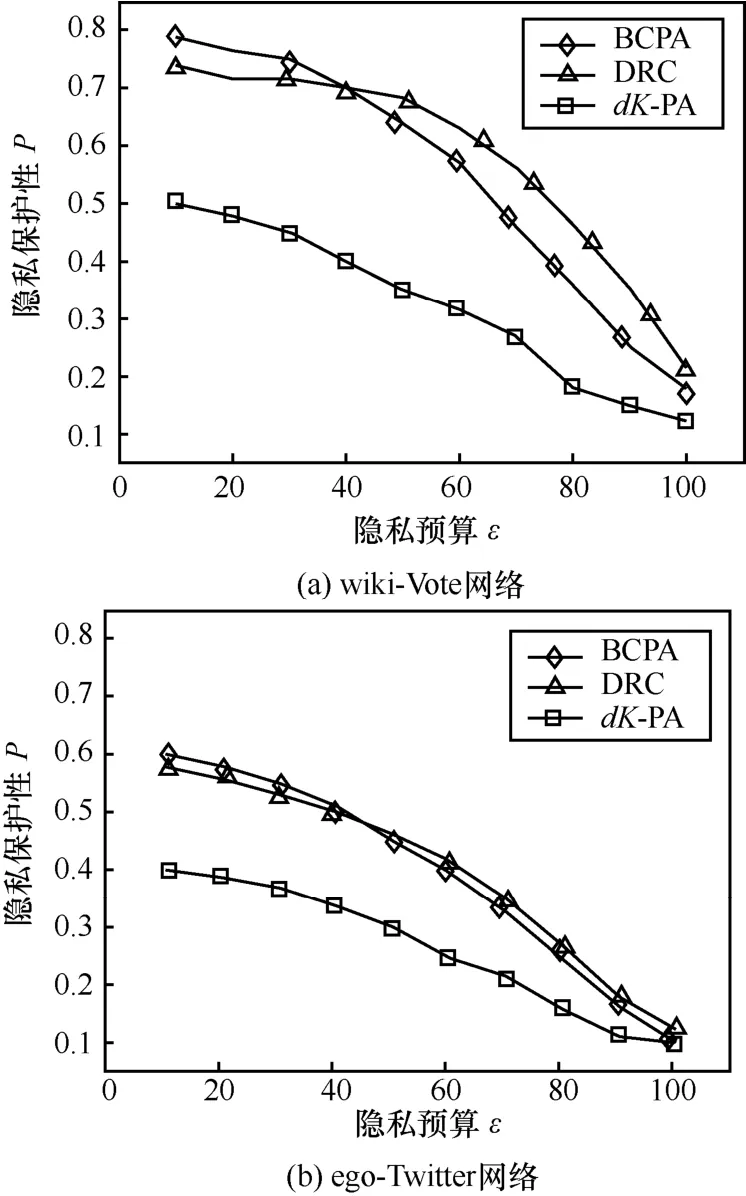
图2 隐私保护性变化趋势

由图2可以看出，在不同ε值和不同大小的数据集中，相比于直接对2K序列进行扰动的dK-PA方案，聚类加噪的BCPA方案和DRC方案都表现出较优异的隐私保护效果。这印证了本文中的理论分析，即聚类后加噪可以更有效地利用隐私预算以达到提高隐私保护强度的作用。BCPA方案和DRC方案在不同的ε值范围下，隐私保护效果各有优劣。无论是在体量较小的wiki-Vote网络中，还是在体量较大的 ego-Twitter网络中，在ε值较小的情况下(ε≤40)，即隐私保护强度较高时，BCPA方案表现更好；而当ε值较大时(ε≥50)，隐私保护强度较弱，此时 DRC方案的效果更胜一筹。这种结果差异性是排序算法不同造成的，2种排序算法基于不同的图属性重组2K序列，导致在根据加噪后的2K序列生成新图时，新图结构的差异在隐私保护性衡量算法中反映出来。值得注意的是，当ε值增加到一定值后(ε＞90)，3种方案的隐私保护效果差别较小，可见引入噪声量较小时，3种方案的隐私保护性能差异不大。综上，在隐私预算较小时，BCPA方案具有更高的隐私保护强度。

4.2 数据可用性评估

对于社交网络图数据而言，数据可用性分析主要是对社交网络的结构特征参数进行分析。本实验通过将原始图与扰动图的特征参数进行比较分析，验证在不同的隐私预算下BCPA方案在数据可用性方面的优势。本实验选择平均聚集系数、平均最短路径和平均度分布这3个重要参数，用于衡量图结构特征。

由于2K序列非常敏感，其需要添加高水平的噪声以提供高级别的隐私保护。然而，非常小的ε值需要引入非常大的噪声值，虽然隐私强度很高，但会导致产生与原始图结构极不相似的合成图。当ε＜1时，对于较大的图，所需的噪声水平过高，以至dK图生成器很难生成与所得到的dK分布匹配的合成图。因此，为了取得较好的实验效果，本文分别生成ε=5、ε=10和ε=100的满足ε-差分隐私的扰动图。

4.2.1 平均聚类系数

在社交网络图中，平均聚类系数的定义为其中，n为图中节点总数，i为图中某一节点，Ci为该节点的聚类系数。网络的平均聚类系数可以很好地表示网络中节点与其相邻节点之间彼此连接的程度，即由3条边连接三点形成的子图三角形在当前完整网络中的密集程度。

由图3可知，在ε值相同的情况下，BCPA方案生成图的平均聚类系数与原始图更相近，而加噪的差分隐私生成图都呈现出同样的趋势：即当ε值不断减小时，生成图的平均聚类系数逐渐增大。这是由于隐私保护需求的增大，引起更多的噪声边和噪声节点的加入，三角形子图密度增大，导致平均聚类系数值变大。

图3 平均聚类系数柱状图

但即使是在ε=5的情况下，2个体量各异的真实社交网络图与BCPA方案生成图之间的差异也没有超过20%，因此，在保证较高隐私保护强度的情况下，BCPA较好地保留了原始图属性。

4.2.2 平均路径长度

由于真实社交网络图数据满足“小世界”特征，即图平均路径长度值为6左右。通过仿真实验比较wiki-Vote网络和 ego-Twitter网络的平均路径长度值与其满足ε-差分隐私的扰动生成图的平均路径长度值，其结果如图4所示。

图4表明，2个真实社交网络图数据的平均路径长度均符合“小世界”特征，而其差分隐私生成图随着ε值的减小，平均路径长度也随之变短。即，随着ε值的减小，隐私保护需求不断增大，所需引入的噪声也随之增多，添加了较大数量的扰动边，导致节点之间的连通路径有了更多选择。因此，平均路径长度随着噪声量的增大而不断减小。

图4 平均路径长度柱状图

由图4可知，对于数据量不同的2个社交网络图数据，BCPA加噪生成图的平均路径长度均更加接近于原始图。因此，在给定隐私预算的情况下，BCPA能够更好地保留原始图的属性，使扰动数据具有更好的数据可用性。

4.2.3 节点度分布

节点度分布是对一个图中节点度数的总体描述，对于本文方案所采用的2K随机图而言，节点度分布就是图中顶点度数的概率分布。节点分布对比如图5所示。

图 5(c)和图 5(f)表明，当ε=100时，由于所引入的噪声量较小，原始图与BCPA和DRC的加噪生成图的节点分布相差不大。而当ε=5和ε=10时，wiki-Vote网络和ego-twitter网络的加噪生成图都与原始图结构有较大差距。出现这种差异的原因是少数高度数节点连接大多数其他节点。因此，当高度数节点引入了噪声时，它会产生向图的其余部分传递波动的结构变化。可见当数据集所含节点数较多时，为实现较好的隐私保护效果，引入的大量噪声显著改变了图结构。

图5 节点度分布对比

此外，由图5可知，在节点度分布属性上，BCPA和DRC的效果明显优于dK-PA，且DRC方案稍好于BCPA方案，但差距不明显。这是由于DRC是根据节点度大小对2K序列进行聚类分组，使加噪生成图的节点度分布更接近原始图。而BCPA是根据中介中心性系数对2K序列进行聚类分组，在原始图中“重要性”相同或相近的节点被聚类在同一子序列中，分组加噪时依然能保证不改变各节点的“重要性”。因此BCPA生成的差分隐私图在平均路径长度和平均聚类系数这2项重要属性上保留了更多的原始图结构特征。

5 结束语

本文针对基于差分隐私的社交网络图数据发布问题，提出一种基于边介数模型的差分隐私处理方案 BCPA，该方案结合dK模型对边序列进行聚类划分，同时考虑到各边在图中的影响力程度，引入边中介中心性系数来显著减少2K序列敏感度。将BCPA方案与DRC和dK-PA方案进行了实验仿真，通过对平均聚类系数、平均路径长度以及节点度分布等指标的对比和分析，在较高隐私需求情况下，BCPA方案的隐私保护性和大部分数据可用性都优于DRC方案和dK-PA方案。下一步可进行以下2个方面的工作：1) 在本文所提算法的基础上，进一步改进 2K序列构造算法而提升运行效率；2) 在隐私需求较高的情况下，在引入噪声量增大的同时，保证数据可用性维持在较高水准。