PLS模型下空气污染影响因素的统计测度——以中原五省为例

常思远

(江苏大学 财经学院，江苏 镇江 212013)

近几年来，空气污染已经成为一个全球化问题，受到全世界各个国家的关注。同样在我国，随着经济的迅猛发展，各地区尤其是我国中原地区都在饱受长时间、大范围雾霾问题的困扰。自“十三五”召开以来，各级政府越来越关注于“绿色发展”，持续加强各行各业的污染减排和末端治理，解决存量污染物治理和生态环境修复等问题。2019年两会同样要求在经济下行压力较大的情况下，环境监管亦不能松懈，需要继续强化生态环境刚性约束。在这样的要求下，中原地区在加快发展的同时如何控制空气污染就成为了需要考虑的问题。基于此，发现对空气污染有显著影响的指标并预测，以求对未来的空气污染状况进行评估与调控就是我们需要解决的问题。为此，本文采用文献分析法和偏最小二乘法，构建出空气污染影响因素的回归模型，确定具有显著影响的指标并预测未来的空气污染状况。

1 国内外学者关于空气污染影响因素和研究方法的研究现状

空气污染影响因素的研究并不是一个新的课题，国内外已有丰富的研究结果，大致将影响因素分为五个方面。经济增长方面，Soumyananda(2004)、李斌和李拓(2014)都通过环境库兹涅茨曲线假说来说明空气污染和经济增长之间的关系是一种倒“U”型关系，前者认为经济发展一开始会加剧空气污染状况，但在到达一个节点后便会减缓空气污染状况。后者借用前者的观点，得出我国正处于“U”型曲线的拐点，即经济增长导致空气污染加剧的时期这样的结论[1-2]。李茜等(2013)认为第二产业结构比例与空气污染物浓度具有明显的正向关系[3]。同时韩楠、于维洋(2015)和吴振信等(2016)也认为第二产业占比对空气污染有着重要影响[4-5]。能源消费方面，Faamd(2001)对欧盟200多个城市和地区进行研究，发现在城市化的过程中，能源消费已经成为影响空气污染的主导因素[6]。王敏和黄滢(2015)对此结论进行概括，说明在高收入地区，随着经济的进一步增长，会导致空气污染的进一步恶化[7]。机动车尾气排放方面，Ghose等(2004)通过对印度大型城市的研究指出，空气污染所产生的空气质量危机主要来源于交通运输过程中产生的尾气排放[8]。高纹(2019)的研究结果同样表明在北上广等超大型城市，机动车所产生的交通尾气排放是当地空气污染的主要原因[9]。技术进步方面，Hixson M等(2010)利用四种不同的技术和手段对地区的空气污染状况进行分析，发现技术会明显影响空气污染的状况[10]。陈平等(2012)、牛海鹏等(2012)认为在治理空气污染的过程中需要考虑到技术进步对空气污染的影响，并且技术创新会对废气排放强度带来比较强的影响[11-12]。政府治污投资方面，徐业傲(2014)的研究结果指出，当治理废气投资增加时，工业废气排放量有下降趋势[13]。而Feinerman E等(2001)用以色列的例子来说明“政府治污投资”的这样一种政策虽然与空气污染有关，但不是人们所想的限制性关系[14]。

在空气污染的研究方法上，Smith R I(1999)利用空气污染统计的方法，确定了英国在不同历史背景下对当时二氧化硫排放量的控制水平[15]。Mei-Li You、Chi-Min Shu、Wei-Ting等(2016)采用灰关联度和灰熵的方法计算日本五大空气污染物所带来的空气质量的下降，以此来说明当地空气污染扩散的趋势，并用这种方法建立各种空气污染的容许限度[16]。姜磊、周海峰、柏玲等(2018)运用自然正交函数分析城市空气质量指数的时空演变特征，并采用基于衰减效应的矩阵指数空间设定模型探讨了空气污染的影响因素[17]。张丽峰(2017)的研究中运用了脱钩理论和VAR模型，分析了北京三类主要空气污染物与经济增长状况之间的脱钩状态、相互间的动态影响和程度[18]。张志威(2017)将因子分析法和聚类分析法结合，对由经济和污染物排放所组成的指标进行综合研究，发现了制约空气质量的关键因素[19]。

本文的研究以我国中原五省的省际面板数据为研究对象，选择偏最小二乘回归方法构建模型，并通过实证分析来得出不同影响因素的影响力大小，最终对未来情况进行预测。与现有研究空气污染影响因素的文献相比，本文的差异有以下两点：一、选用的数据量大且具有针对性，可以较为科学的得出影响该地区空气质量的因素；二、可以通过最后得出的模型进行预测，以帮助人们更好地应对未来的空气污染状况，起到一定的评估和预警作用。

2 偏最小二乘回归模型的构建

偏最小二乘回归模型是一种相对较新的多元统计分析方法，自从1983年它首次被提出后就受到了广泛的应用。偏最小二乘回归模型是结合了多元线性回归、主成分分析和典型相关分析三种方法的优点而得到的模型方法，它不仅可以解决变量间的多重线性相关问题，也可以解决在回归分析中样本数量少于变量数量的问题。同时在回归建模中，可以做到简化数据结构、使变量间的相关分析变得简单和进行预测。

偏最小二乘回归首先在X和Y中提取成分t1和u1。在提取这两个主成分时，要求t1和u1要尽可能携带它们各自数据矩阵中的变量信息并且t1和u1的相关程度能够达到最大。只有这样，t1和u1才能既最大化代表数据表X与Y，同时又保证自变量成分t1对因变量成分u1有最好的解释能力。

在第一个成分t1和u1被提取后，分别实施X对t1的回归以及Y对t1的回归。因为此时数据已经做到各成分之间不存在完全的共线性，可以进行回归。如果变量间的回归方程已经达到了满意的程度，计算就会停止；否则，将利用X被t1解释后的剩余信息以及Y被t1解释后的剩余信息进行第二次的成分提取。如此循环下去，直到能达到一个比较满意的精度为止。

选用多少个成分通过交叉有效性来判断。定义预测误差平方和为PRESS，交叉有效性为

当Qh2≥(1-0.952)=0.0975时，th成分的边际贡献是显著的，该th就需要被使用。

如果最终对X提取了m个成分t1,…,tm，偏最小二乘回归将通过yk对成分t1,…,tm的回归，再表达成yk关于原变量x1,…,xp的回归方程，k=1,2…,q。最后得到的方程结果应为如下形式

yk=β0k+β1kx1+β2kx2+……+βpkxp+εk,k=1,2,…,q

3 变量的选取与处理

在构建模型的准备阶段，我们需要对变量指标进行选取。在能够表示空气污染状况的因变量的选取上，我们选取了二氧化硫排放量、氮氧化物排放量和烟(粉)尘排放量作为因变量进行模型构建。

在自变量的选取上，本文选取了地区国民生产总值、固定资产投资和第二产业占比作为表示经济增长的指标，选取了煤炭消费量和原油消费量作为能源消耗指标，以公路里程、民用汽车拥有量和私人汽车拥有量作为反映机动车尾气排放的指标，以经费投入强度、技术市场成交额和规模以上工业企业有效发明专利数作为技术进步的指标，最后以治理废气项目完成投资作为政府治污投资指标。

在选取变量的过程中，由于各个省份的人口数量不同，地区国民生产总值总量的不同，单纯地比较各个变量的绝对值容易产生误差，故所选取的变量都进行了初步的处理。其中治理废气投资强度是采用治理废气投资额与地区国民生产总值的比值，民用车数、私人车数和有效专利件数若采用人均值则数值太小，不方便模型计算，故采用万人平均处理，其他的变量均采用人均数值。另外在模型的计算中，为了避免量纲和数量级的不同，我们对数据都进行了标准化处理。

本文的研究对象为中原五省的空气污染影响因素，故在选取指标时以中原五省为基础，选择了2011年—2017年七年的面板数据为样本进行模型构建。表1为最终采用的空气污染状况指标体系。

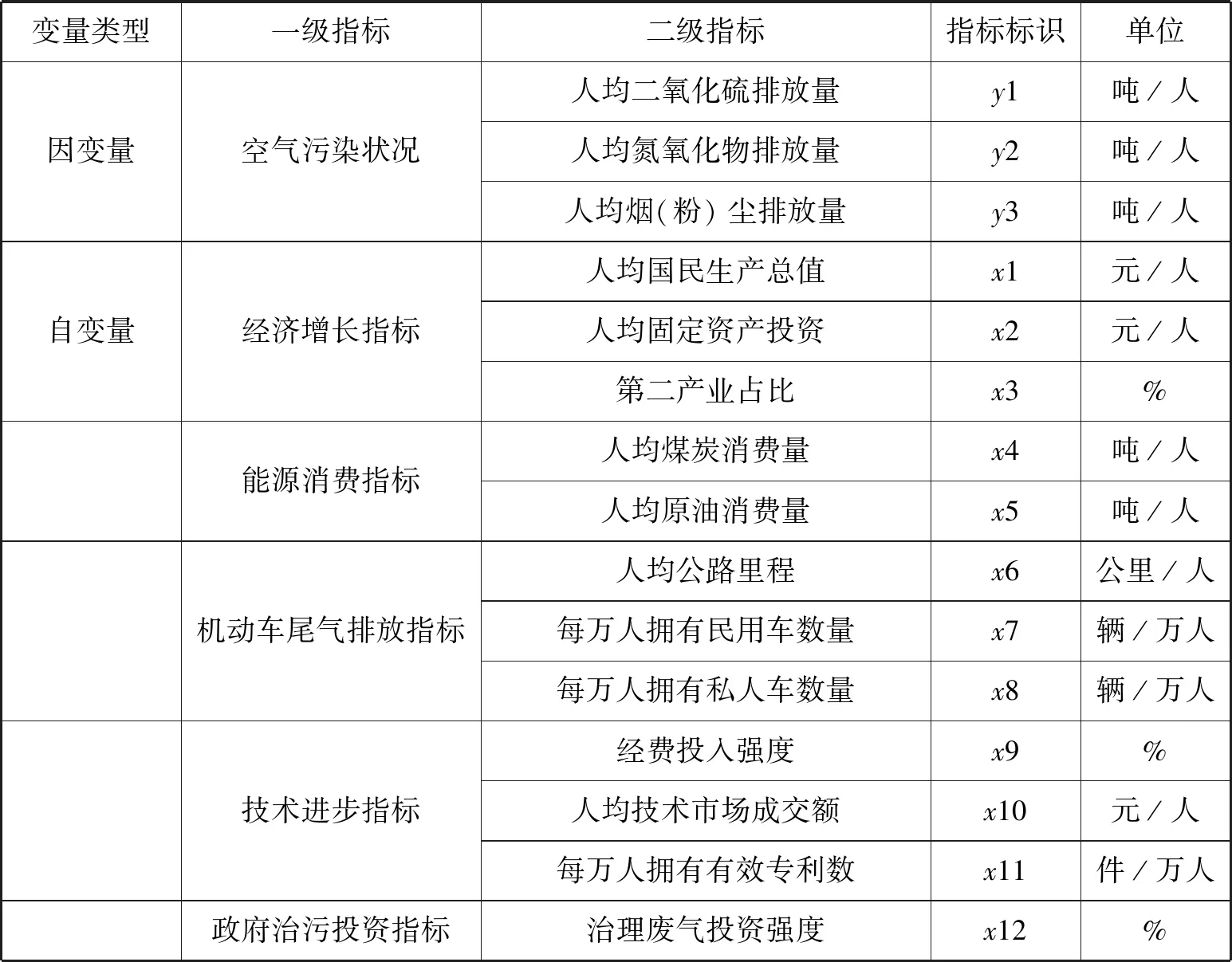
表1 空气污染状况指标体系

4 实证分析

(一)偏最小二乘回归模型的检验

在最终构建模型方程之前，我们需要对偏最小二乘回归模型的结果进行检验，来判断模型的拟合效果是否良好。首先是线性相关性检验，利用的是t1/u1平面图，其中t1是自变量组的第一偏最小二乘成分，u1是因变量组的偏最小二乘成分，如图1所示:

图1 平面图

从图中我们可以看出u1和t1之间呈现较为明显的线性关系，说明在模型中所选取的两组变量存在较强的相关关系。这样我们可以认为模型中所选取的变量是合理的。

接着进行的是回归模型的精度检验，通过累计解释能力来判断。当交叉有效性大于0.0975时成分提取终止，再通过所选取的成分的累计解释能力来判断模型的精度。表2为模型的精度分析

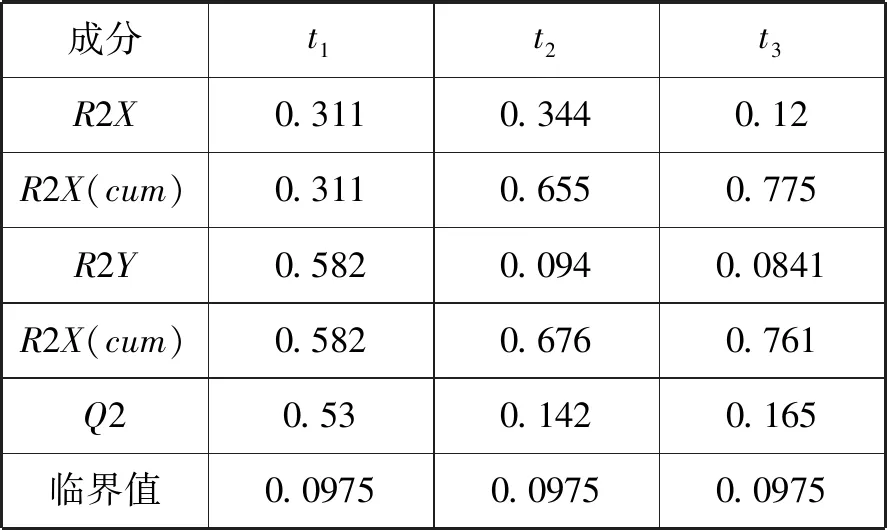
表2 空气污染影响因素的偏最小二乘回归的精度分析

表2中，符号R2X表示成分th对X的解释能力，R2X(cum)表示成分t对X的累计解释能力；符号R2Y表示成分th对Y的解释能力，R2Y(cum)表示成分t对Y的累计解释能力。Q2值则为交叉有效性，临界值取0.0975。当成分的交叉有效性小于0.0975时成分选取终止，所以最后选择了三个成分。从表2数据来看，三个成分对X组自变量的信息利用率为77.5%，并且能够解释76.1%的Y组因变量，二者的解释能力都大于了75%，说明模型提取的成分结果很好。

再次进行的th是的成分解释。通过t1、t2、t3与原变量xj与yk的相关系数平方表来解释，如表3所示:

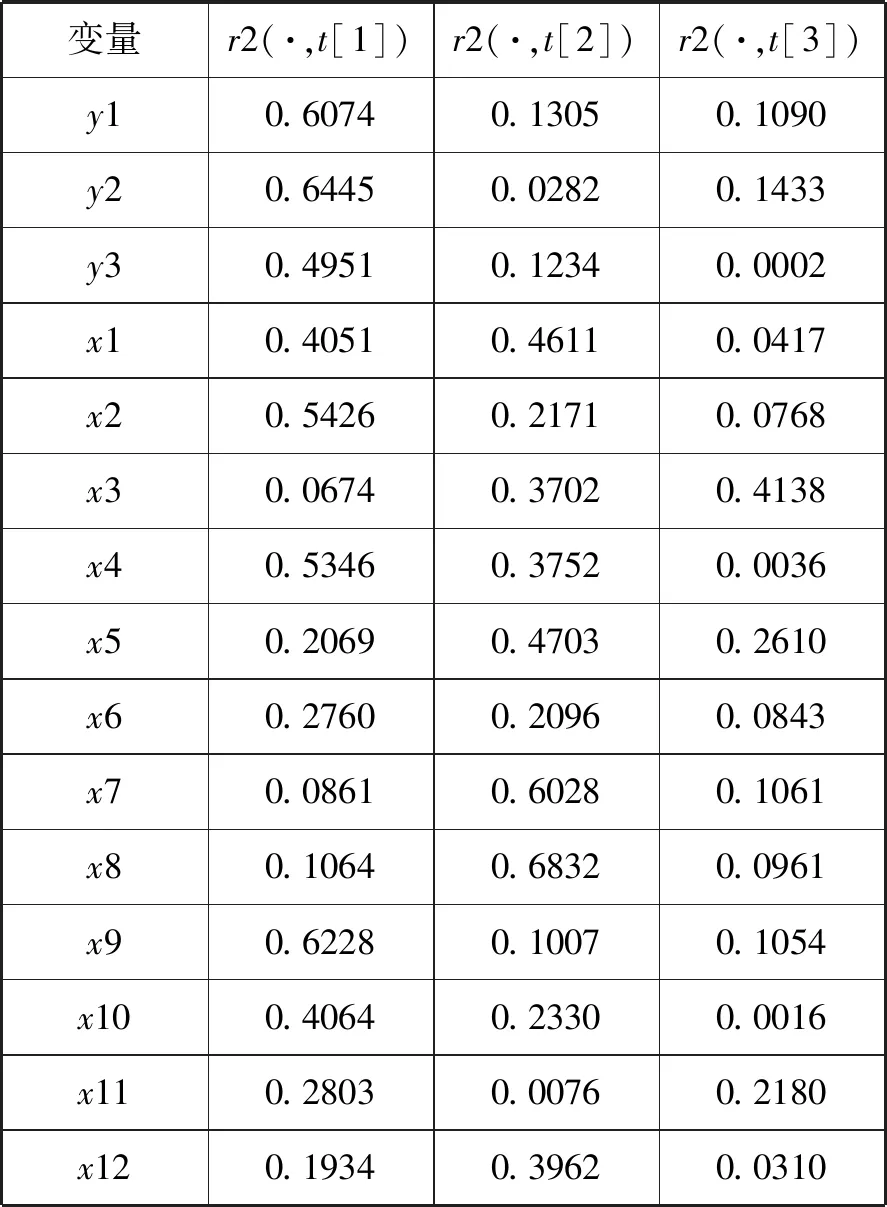
表3 空气污染影响因素的t1、t2、t3与原变量的相关系数平方表

从表中可以看出，t1与人均固定资产投资、人均煤炭消费量、经费投入强度和人均技术市场成交额呈强相关，t2与人均国民生产总值、人均原油消费量、每万人拥有民用车数量、每万人拥有私人车数量和治理废气投资强度呈强相关，t3则与第二产业占比呈强相关。

(二)预测模型

通过上述对模型的检验和初步分析可以发现我们模型的建立是合理，接下来便可以通过计算得出模型的最终结果并进行预测。最终的回归模型系数表如表4所示：

表4 空气污染影响因素的回归模型系数表

通过回归模型系数表我们可以得到最后需要的模型方程

y1=1.6665-0.0873x1+0.3961x2

+0.4337x3+0.8811x4-0.3081x5-0.1584x6

+0.1041x7-0.3652x8-0.0583x9+0.1794x10

-0.1384x11-0.0150x12

y2=2.4775-0.1510x1+0.5049x2

+0.5093x3+0.9378x4-0.3075x5-0.0079x6

+0.1344x7-0.5243x8-0.0895x9+0.2200x10

-0.0925x11-0.0301x12

y3=1.3861-0.2358x1+0.7682x2

+0.3738x3+1.0369x4-0.1983x5-0.0420x6

+0.2874x7-0.5523x8-0.1755x9+0.2477x10

-0.0899x11-0.0723x12

通过我们最后得到的回归模型，我们就可以对未来进行预测，如当我们拥有自变量未来的数据时就可以预测未来的空气污染情况。为了检验我们模型的预测效果，我们通过对已有数据的观测值和预测值的比值画出观测值/预测值图来判断，如图2(a)、图2(b)和图2(c)所示

图2(a) 二氧化硫排放量的观测值/预测值图

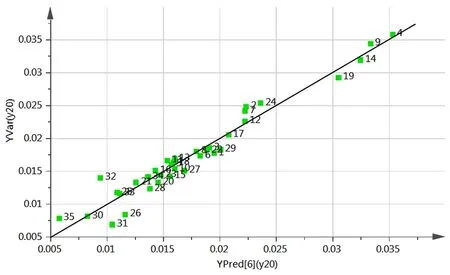
图2(b) 氮氧化物排放量的观测值/预测值图

图2(c) 烟(粉)尘排放量的观测值/预测值图

图中的直线为坐标系的对角线，当预测结果好时，则所有点都会靠近这条线。如此，从三张图中可以看出我们的预测结果很好，可以进行较为准确的预测。

5 结语

根据偏最小二乘回归模型的结果可以看到，对于二氧化硫排放量来说，从系数绝对值来看，煤炭消费量的影响最大。紧接着固定资产投资、第二产业占比和原油消费量这些指标也有较大的影响。对于氮氧化物排放量来说，同样从系数绝对值来看，煤炭消费量的影响最大。紧接着固定资产投资、第二产业占比和原油消费量这些指标同样也有较大的影响。对于烟(粉)尘排放量来说，人均国民生产总值、每万人民用车拥有量和人均技术市场成交额的系数绝对值较大，说明这些指标对烟(粉)尘的影响显著。同时也说明，原油的消费主要造成的是二氧化硫和氮氧化物的排放，对烟(粉)尘的影响较小。

从相关系数平方表中我们可以看到，对空气污染影响最大的因素应该是固定资产投资、煤炭消费量、经费投入强度和技术市场成交额。若想对空气污染状况进行控制，那么就需要从影响最大的几项因素指标入手来达成目的。

综上分析，中原五省在发展经济过程中要控制空气污染的程度，需要对上文提到的有较大影响的变量指标进行综合调控。如在固定资产投资加速的情况下，需尽可能减少煤炭消费量，加大治污经费投入，特别是发展治污技术，并促进技术市场发展，使得技术在经济发展中起到主导作用。本模型也可用于对空气污染状况进行预测。