广义大型互联线性系统的分散迭代学习控制

杜莉莉， 傅 勤*， 顾盼盼， 李向东

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.华南理工大学 自动化科学与工程学院，广东 广州 510640）

自从Arimoto 等人[1]首次提出完整的控制算法以来，迭代学习控制（Iterative Learning Control，简称ILC）已成为近年来控制理论研究的热点问题，并引起人们的广泛关注[2-3]。迭代学习控制适用于在有限时间区间内具有重复运动性质的受控系统，通过反复迭代修正，使得系统的输出轨迹沿迭代轴方向收敛于给定的期望轨迹。

广义系统是一类较正常系统形式更为一般化的动力系统，被广泛应用于电子网络、经济系统、社会系统、生物系统等领域中[4-7]。近年来，许多具有重复运动性质的实际问题，例如工业机器人等[8-9]，都是由广义系统模型来刻画的，由此，研究广义系统的迭代学习控制问题是有意义的。由于广义系统含有正常系统所不具有的脉冲项，对其学习控制设计时，会较正常系统困难些。借助于广义系统的正则性条件，文献[10-13]讨论了线性广义系统的迭代学习控制问题，并给出相应的收敛性条件。最近，文献[14-15]基于矩阵奇异值分解，将广义系统转化为等价的微分代数系统，并在通常的初值假设条件下，给出一种由D 型算法和P 型算法混合而成的新型学习律（称之为D-P 型），有效地解决了线性广义系统的状态跟踪问题。这种新算法无需依赖系统的正则性条件，因而使用起来也较为简单实用。

大型互联系统是由互相关联的子系统组成的一个复合系统，在许多实际控制问题中，系统模型都具有大系统形式。由于其实现的可靠性、实时性和经济性，分散控制已成为大型系统理论中一个活跃分支[16]。在这种分散控制方案中，每个子系统的控制器仅依赖于该子系统的状态变量，不需要与其他子系统交换信息，利于工程实现。近年来，大型互联线性系统的分散控制设计得到了较为深入的研究[17-18]。最近，基于迭代学习控制的大型互联系统的分散控制问题引起了大家的关注，文献[19-23]研究了大型互联系统的分散迭代学习控制问题。

广义大型互联系统是由广义系统互联而成的一类复合系统。文献[24-25]借助于分散控制方法，讨论了广义大型互联系统的稳定性和镇定设计问题。然而，由于广义大型互联系统的复杂性，就迭代学习控制设计而言，尚未涉及到广义大型互联系统。笔者提出广义大型互联线性系统的迭代学习控制问题，研究一类广义大型互联线性系统的分散迭代学习控制，借助于文献[14-15]中采用的矩阵奇异值分解方法，将该类广义大型互联线性系统转化为等价的微分代数系统，再将转化后的系统输入与状态写成矩阵形式，通过构建分散型的D-P 型学习控制算法，说明迭代系统的状态沿迭代轴方向一致收敛于给定的期望轨迹。

文中给出如下符号约定：对矩阵Bi∈Rmi×ni，B＝blockdiag（B1，B2，…，BN）表示块对角矩阵；对矩阵A∈Rn×n，记||A||为矩阵A 的2-范数，即其中ρ（ATA）为矩阵ATA 的谱半径；对向量定义x（t）的上确界范数这里||x（t）||为x（t）的2-范数；对给定的λ＞0，定义x（t）的λ-范数由文献[26]可知，范数||x（t）||S与||x（t）||λ是等价的，即可用其中任一种范数证明收敛性结果。记I 为单位矩阵。

1 问题描述

考虑如下具有重复运动性质的广义大型互联线性系统[24-25]

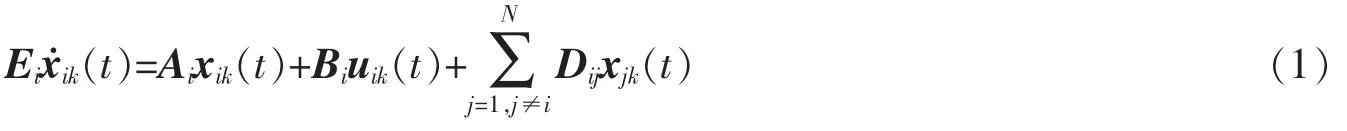
这里i＝1，2，…，N 表示各个子系统，t∈[0，T]。xik（t）∈Rni，uik（t）∈Rmi分别为第i 个子系统在第k 次重复运动时的状态、控制输入，Ei∈Rni×ni是奇异矩阵，且rank（Ei）＝ri＜ni，Ai∈Rni×ni,Bi∈Rni×mi，Dij∈Rni×nj是实矩阵。记

对于给定时间区间t∈[0，T]上的期望轨迹xid（t），学习控制的目的是设计适当的学习律，使得当迭代次数k→∞时，系统的状态序列xik（t）在t∈[0，T]上收敛于理想的状态xid（t），即其中eik（t）＝xid（t）-xik（t），i＝1，2，…，N。

对系统（1）作出如下假设条件：

假设1对于给定的期望轨迹xid（t），存在uid（t），使得

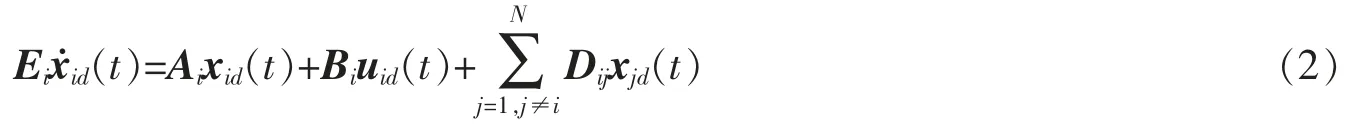
成立，i＝1，2，…，N。

假设2每次迭代时，系统的初始状态取为固定值xid（0），即

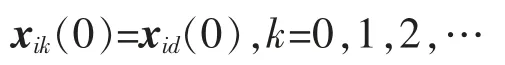
其中，k 为迭代次数，i＝1，2，…，N。

注1假设1、2 是研究迭代学习控制问题的常用假设条件。

价形式式中i＝1，2，…，N。将上式写成矩阵形式，有

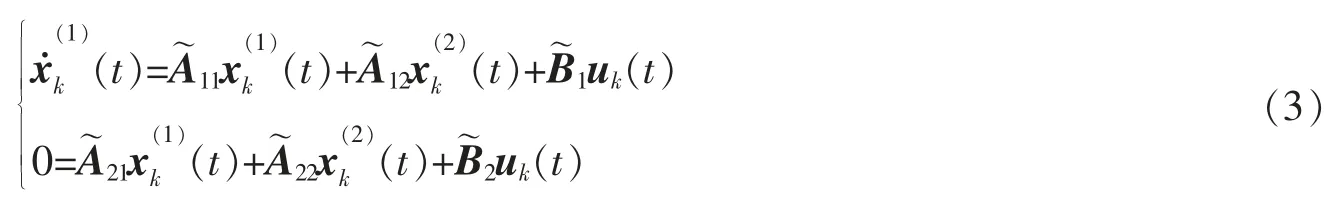
其中

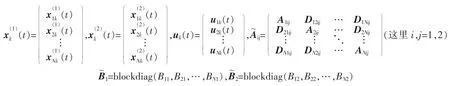
2 学习算法

文中采用如下形式的D-P 型迭代学习控制算法[14]

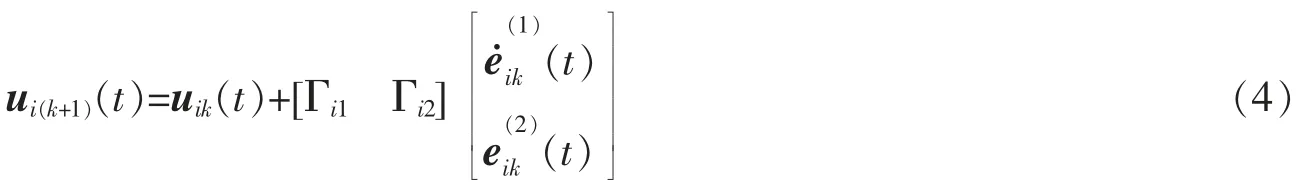
记Δuik（t）＝uid（t）-uik（t），由（4）式可得

再记Δuk（t）＝（Δu1k（t）TΔu2k（t）T…ΔuNk（t）T）T，则

注意到系统（1）与（3）等价，下面对系统（3）给出文中的主要结论及相应证明。

定理1假设1、2 及（4）式成立，若可逆且存在增益矩阵Γ1、Γ2使得

证明因为可逆，系统（3）中第二式可化为

（7）式与（9）式相减，可得

（8）式与（10）式相减，可得

将（11）、（12）式代入（5）式，有

对（13）式两端取λ－范数，可得

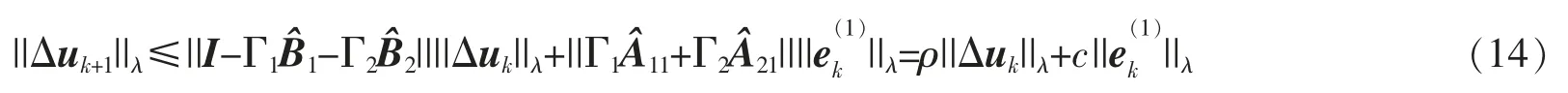
将（8）式和（10）式两端都对变量t由0到t积分，有

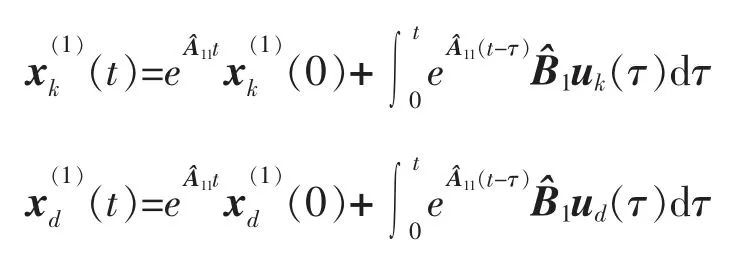
两式相减，并利用假设2 得

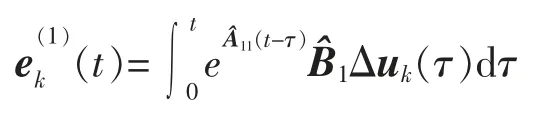
上式两端取2-范数，有

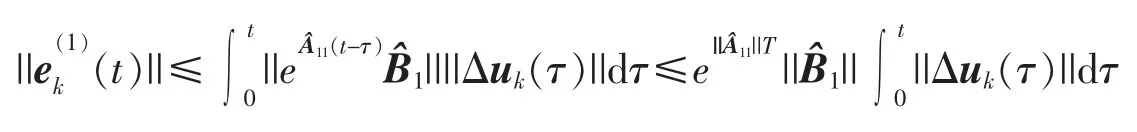
上式两端同乘e-λt，则

由λ－范数的定义知

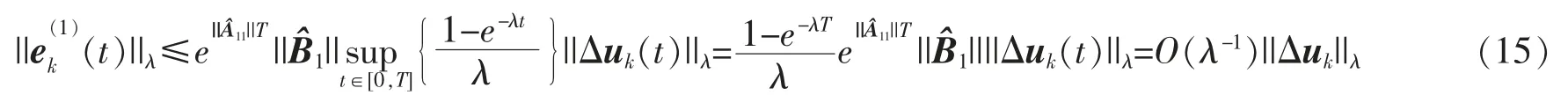
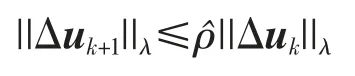
结合（15）式和（16）式，可以得到

由于

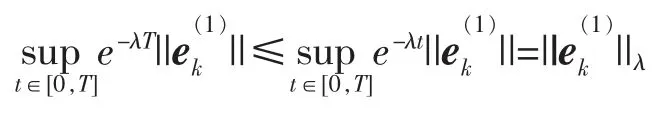
即

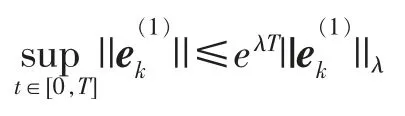
从而

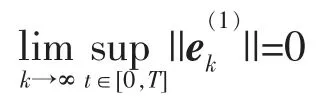
由2-范数和上确界范数的定义，可得

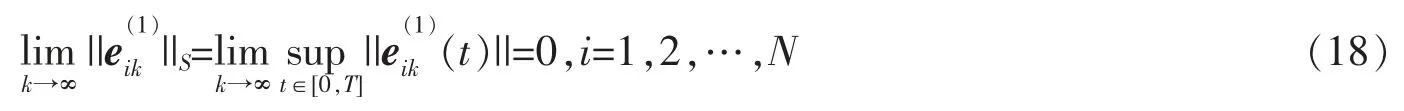
另一方面，（11）式结合（16）、（17）式，有

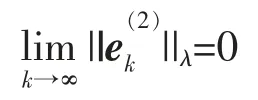
类似于（18）式的推导，有

结合（18）、（19）式，可知

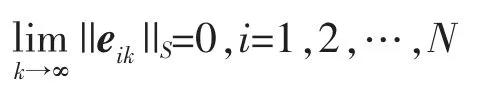
证毕。

3 仿真算例

考虑如下形式的广义大型互联线性系统

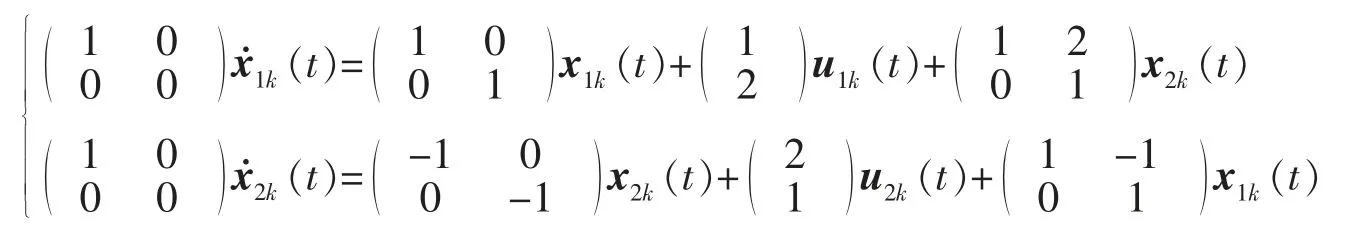
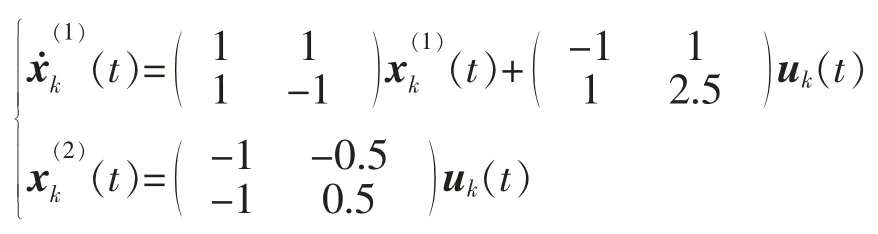
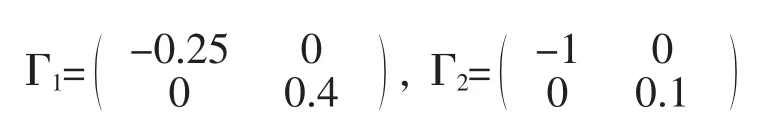
对给定的期望轨迹

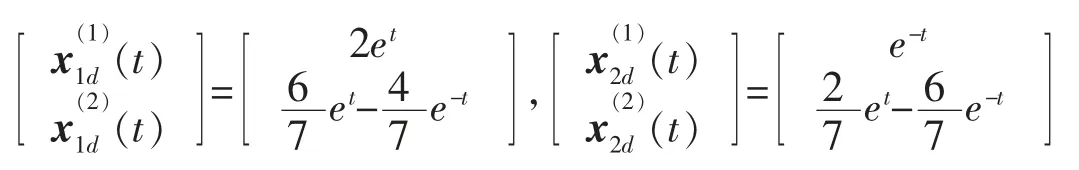
取初始控制u10（t）=u20（t）=0。在学习算法（4）式的作用下，利用Mathematica 软件进行仿真分析，得到图1 和图2。

图1 x1k 的跟踪误差

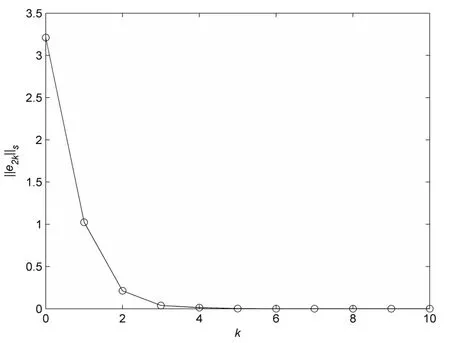
图2 x2k 的跟踪误差

图1 和图2 分别表示子系统1 和2 的状态跟踪误差随迭代次数变化曲线，从图中可以看出，随着迭代次数的增加，广义大型互联线性系统的各个子系统的状态跟踪误差在学习算法（4）式的作用下沿迭代轴方向趋近于零。

4 结语

文中研究一类广义大型互联线性系统的状态跟踪问题。利用矩阵奇异值分解的方法，将广义大型互联线性系统转化为等价的微分代数系统。针对微分代数系统，构建得到一种D-P 型的迭代学习控制算法。理论分析表明，所给算法在一定条件下是收敛的，经过不断迭代，系统的状态能渐近的跟踪期望轨迹。同时，仿真算例也说明了算法的有效性。