带内饰车身噪声传递函数优化分析

邢秋颖 刘鹏 孙寿峰 苏辰

（中国第一汽车股份有限公司天津技术开发分公司）

随着汽车设计水平及生产技术的不断提高，以及各级供应商和整车厂之间合作的日益紧密，不同品牌汽车的使用性能和安全性能间的差异越来越小。相比之下，汽车的舒适性成为区分汽车品牌好坏的重要因素之一[1]。车身内的振动和噪声是衡量乘坐舒适性的重要指标，因此，控制汽车噪声成为现代汽车开发过程中重要的控制目标之一。文章从车身的角度对噪声传递函数进行了分析。噪声传递函数（NTF）是指在一个系统中，输出噪声（如驾驶员右耳声压）与输入激励载荷（如在车身关键接附点施加振动激励）的比值。换言之，输入激励与噪声传递函数的乘积就是输出噪声值，那么在激励一定的情况下，可以通过减少噪声传递函数降低车内的结构噪声[2]。文章利用HyperMesh 前处理软件和MSC.Nastran 求解器进行NTF 分析，通过对噪声传递函数中的超标峰值进行分析，从而优化噪声传递函数，减少车内结构噪声，提升车身的NVH 性能。

1 车内结构噪声[3]

车内结构噪声一般是由发动机和外界激励通过传动系统和悬架传递到车身板件上，激起车身板件的振动，引起车内声腔体积的变化，造成声压的波动从而产生噪声。与此同时，声腔内空气的运动也会作用到车身上，激起板件的振动，因此，车身板件和声腔之间相互作用。结构和流体之间的耦合关系可用一个耦合矩阵（R）来表示。

板结构施加在流体上的力的关系式，如式（1）所示。

F1——板结构施加在流体上的力，N。

流体作用在板结构上的力的关系式，如式（2）所示。

式中：Ff——流体作用在板结构上的力，N；

Q——声腔的声压，Pa。

对于封闭空间，空气有一定的质量、刚度和阻尼，声压是时间和空间的函数。将封闭空间分成若干个小空间进行离散，则流场内的波动方程可以写成有限元矩阵方程，如式（3）所示。

式中：Mf——流体等效质量矩阵；

Cf——流体等效阻尼矩阵；

Kf——流体等效刚度矩阵；

P——各节点的声压向量；

如果将车身板件的振动输入加到声腔上，则得到关系式，如式（4）所示。

板结构受到的激励包括来自发动机和底盘等系统的外界激励（Fs/N）以及Ff。则板结构振动的动力学方程，如式（5）所示。

式中：Ms——结构等效质量矩阵；

Cs——结构等效阻尼矩阵；

Ks——结构等效刚度矩阵；

U——板结构的振动位移，mm；

将式（4）和式（5）写成 1 个矩阵方程组，得到关系式，如式（6）所示。

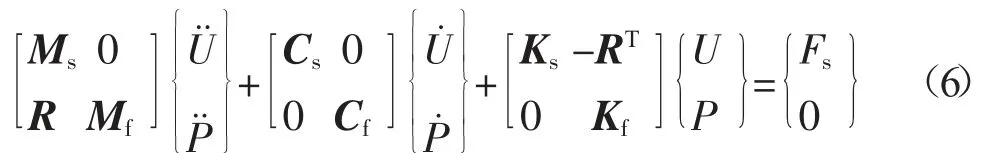
声腔与车身板件的耦合分析主要是计算车身板件的振动对车内声腔的影响，其主要应用在3 个方面：

1）体现声腔内声压变化的特征。板结构振动推动声腔内空气，导致声压变化，这是分析车内结构噪声的基础。

2）找到引起车内轰鸣的板结构。板件振动的频率与声腔频率接近时会发生共振，产生车内轰鸣声，所以找到引起共振的板件并改进其结构才能有效地控制轰鸣声。

3）进行板件的贡献量分析，即分析众多与声腔接触的车身板件对车内声压的贡献，从而找到主要贡献源，通过改变结构降低车内噪声。

2 分析模型

噪声传递函数的模型包括一个带内饰的车身模型和声腔模型，如图1所示。带内饰的车身模型包括白车身、动力总成悬置、四门两盖、座椅总成、转向系统、副车架和车身内外饰，主要采用四边形和少量三角形壳单元划分网格。焊点采用ACM 单元模拟，焊缝采用CWELD 单元模拟，胶粘采用实体和RBE3 单元模拟，车门密封采用RBE2-CBUSH 单元模拟，衬套和车门锁采用CBUSH 单元模拟，螺栓采用RBE2 单元模拟，内外饰件采用集中质量模拟。车内声腔模型包括空气腔和座椅声腔两部分。声腔采用四面体单元进行离散，材料属性为流体，采用MAT10 来定义。

图1 车身噪声传递函数模型图

整个分析模型不施加任何约束，为自由状态，在车身和底盘的20 个主要接附点处分别施加X，Y，Z 3 个方向大小为1 N 的扫频激励，扫频范围是20～200 Hz，TB 模型分析频率范围是0～300 Hz，声腔模型分析频率范围是0～600 Hz，采用模态频响法计算单位载荷下驾驶员右耳侧的声压变化曲线。

3 结果分析与优化

通过模态频率响应分析得到驾驶员右耳侧噪声频响曲线，经与目标曲线对比，对不满足设计目标的曲线进行统计和分析。通过观察发现，所有不满足设计要求的频响曲线存在2 个特点：1）超标声压值对应频率范围集中在两部分，分别为24 Hz 附近以及130～170 Hz范围内；2）130～170 Hz 范围内不满足设计要求的噪声频响曲线输入点均集中在副车架上。对不满足设计要求的接附点噪声传递函数进行原因分析，一般分析方法有接附点动刚度分析、模态贡献量分析及钣金贡献量分析法。

3.1 原因分析

结合不满足设计要求的频响曲线的2 个特点，以前控制臂左前安装点为例进行噪声传递函数优化分析。前控制臂左前安装点Z 向激励下的噪声传递函数，如图2所示。Z 向单位激励下的NTF 曲线在24 Hz附近、160～190 Hz 频带范围内超出目标值，其中在24 Hz和162.5 Hz处有较高峰值，风险较大，需要进行优化分析。

图2 车身前控制臂左前安装点Z 向噪声传递函数曲线图

3.1.1 动刚度分析

前控制臂左前安装点Z 向动刚度曲线，如图3所示。24 Hz 附近动刚度满足设计要求，160～190 Hz 频带范围内该点动刚度不满足目标值。结合该点噪声传递函数分析，该点动刚度低是噪声超标的原因之一。

图3 车身前控制臂左前安装点Z 向动刚度曲线图

3.1.2 模态贡献量分析

前控制臂左前安装点在24 Hz 结构模态贡献量分布，如图4所示，贡献量最大的为第20 阶24.34 Hz，贡献最大比例为201.73%。图5 示出第20 阶车身模态振型图。从图5 可以看出，后背门和翼子板变形较大。由于翼子板结构单一、修改空间较小且不与声腔直接接触，可以从修改后背门处刚度入手改变频率大小。声腔模态贡献量最大的为第1 阶、第2 阶和第3 阶模态，贡献比例依次为76.37%，19.37%，9.30%，车身结构固定后，声腔结构很难修改，所以声腔模态几乎不能改变。

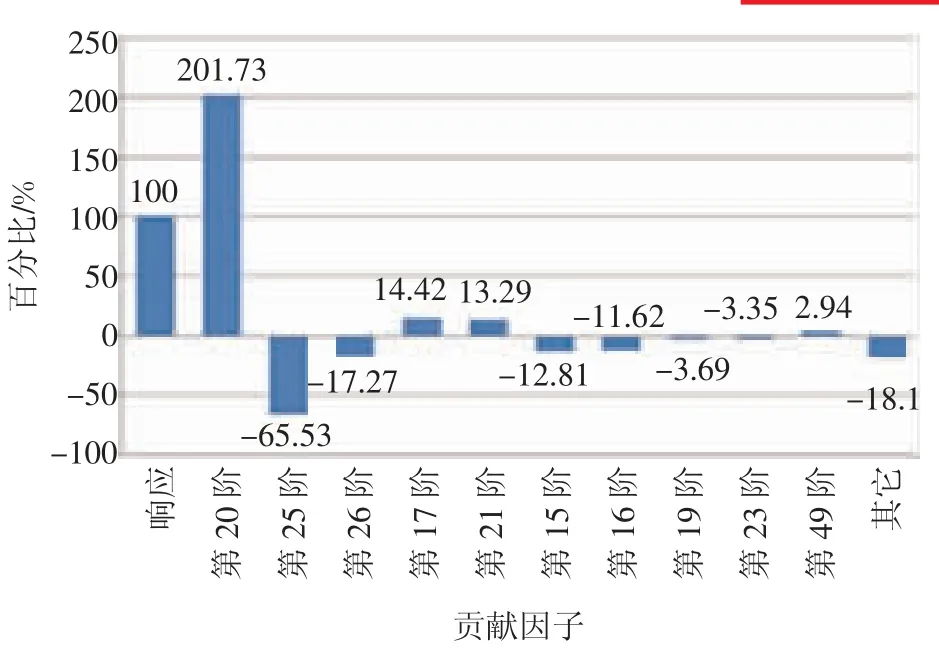
图4 车身前控制臂左前安装点在24 Hz 结构模态贡献量分布图

图5 第20 阶车身模态振型图

前控制臂左前安装点在162.5 Hz 结构模态贡献量分布，如图6所示。贡献量较大的依次为第491 阶165.38 Hz，第 498 阶 167.54 Hz，第 366 阶 138.46 Hz，贡献比例依次为21.75%，15.21%，14.65%。从以上三阶模态振型看，很难找到修改方向，但是这三阶模态中均存在副车架的整体模态，如图7所示。可以考虑从副车架入手。声腔模态贡献量最大的为第7 阶、第10 阶和第5 阶模态，贡献比例依次为53.6%，19.04%，14.28%，声腔模态很难变更，所以不考虑改变声腔频率。

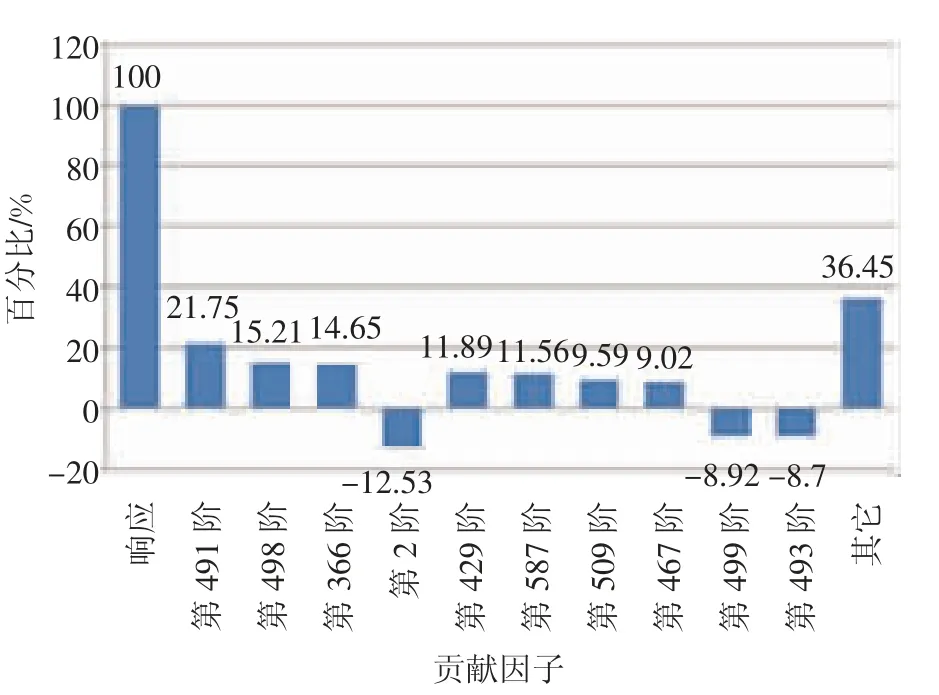
图6 车身前控制臂左前安装点在162.5 Hz 结构模态贡献量分布图

图7 贡献量较大的三阶副车架模态振型图

3.1.3 面板贡献量分析

前控制臂左前安装点在24 Hz 的面板贡献量依次为后背门内板75.63%，后风挡玻璃36.48%和备胎壳-26.12%。后风挡玻璃不能修改，所以不予考虑。备胎壳对车内声压为负贡献，即备胎壳产生的声压与车内总体声压反向，车内声压会随备胎壳振动幅值的升高而降低。后背门内板与声腔直接接触，其振动对声腔内声压变化有直接影响，且从面板贡献量看，后背门内板的振动对车内声压影响最大。

前控制臂左前安装点在162.5 Hz 的面板贡献量依次为车顶棚25.59%，左前车门玻璃20.40%和右前地板18.91%。从面板贡献量分布图观察，每块面板对声压的贡献量相差不多，说明在162.5 Hz 每块面板对车内声压贡献比较平均，没有突出贡献的板块，在面板改进方面找不到突出方向。

3.2 NTF优化分析

3.2.1 针对24 Hz 处峰值问题的NTF 优化分析

综合结构模态贡献量和面板贡献量分析，问题均体现在后背门位置，可以从提高后背门刚度入手。查看TB 模型的第20 阶模态中，后背门相对车身具有较大的开合位移，所以从提高后背门与车身的连接刚度方面优化，经过多次分析得到最终优化方案，如图8所示。修改车身侧后背门锁环加强板的结构，同时增加与车身的焊点，优化后效果，如图9所示。24 Hz 处噪声峰值有明显下降，且满足目标值。

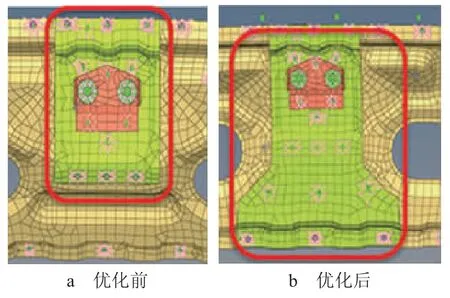
图8 24 Hz 处车身噪声峰值问题的优化方案示意图

图9 24 Hz 处车身噪声峰值问题优化方案NTF 曲线图

3.2.2 针对162.5 Hz 处峰值问题的NTF 优化分析

针对162.5 Hz 处峰值问题，可以从提高副车架接附点动刚度入手。结合不满足设计要求的频响曲线存在的特点2，改变副车架与车身的连接方式，将用弹簧单元模拟的衬套连接改为刚性连接。优化后效果，如图10所示。160～190 Hz 频带内，噪声峰值有明显下降，且满足目标值。

图10 162.5 Hz 处车身噪声峰值问题优化方案NTF 曲线图

3.2.3 最终NTF 优化分析结果

以上2 个优化方案对于降低车内噪声都起到了很好的作用，现将2 个方案合并，合并后效果，如图11所示。24 Hz 处的噪声峰值（56.2 dB）下降了5 dB；162.5 Hz 处的噪声峰值下降了7 dB。

图11 前控制臂左前安装点Z 向最终优化方案NTF 曲线图

4 结论

文章采用动刚度分析、模态贡献量分析和面板贡献量分析3 种方法并结合所选车型的NTF 曲线特点，系统地分析了噪声产生的原因，有针对性地采取了优化方案，使超标工况从最初的30 个下降到12 个，达到了突出的优化效果。NTF 问题是一个由多种原因引起的复杂的工程问题，与结构模态和声腔耦合，及原点动刚度相关。通过NTF 问题曲线能准确找到问题所在，并通过以上方法确定峰值产生的原因，可有针对性地进行优化，解决实际工程问题。