基于函数模型思想下的一次函数教学

贾云

在初中代数教学中，函数教学是重要内容。学习函数应重视其对现实世界变量之间关系的刻画作用，及模型的作用。一次函数是函数学习中重要组成部分，一方面由于一次函数的知识是建立线性拟合（线性模型）的基础，现实生活中建立这种模型的问题的模型是大量存在的;另一方面对一次函数的学习将使学生初步体验研究函数的一般方法。在教学中如何培养学生如何灵活正确理解一次函数的基本性质及一次函数所反映的现实对象之间的关系，能运用语言、式、数值、图像描述和解释数量关系与变化规律，用模型的方法把认识与应用提高到一个高的水平。帮助学生养成良好的数学思维习惯，合理构建函数模型解决问题的重要能力是教师教学中应注意的重要课题。就此谈谈我的体会。

1 基于函数基本知识与基本技能建立恰当的函数模型

函数作为刻画现实世界中变化规律的主要的数学模式。模型的建构必须依托于现实世界中的问题情景，反映了实际问题中“量”与“量”之间的关系。这样的关系成为一种相互依赖关系，对函数自身及表达方式（列表法、图像法、解析法）的理解，是落实函数基础知识和基本技能等是教学的落脚点

1.1 基于表格呈现变量之间的关系建立函数模型

现实世界中存在大量问题，具有简单函数关系的变量，其中大多为变量之间的单值对应关系，属于初中数学研究函数的范畴。列表法。只为表达变量间的单值对应关系常用的方法。表格呈现实际问题中的变量之间的对应关系，再结合变量值的对应类型。确定的对应关系，进而再根据对应关系回到实际情景之中，分析变量的实际意义，建立恰当的函数模型。以表格方式所记录的对应关系，具体的反映出函数是刻意刻画同一变化过程中两个变量之间的单值对应关系的模型思想内涵。

1.2 基于图像表达变量之间的内在联系建立函数模型

以图像的方式，可以使函数所表达的数量之间的对应关系，更加形象、直观，为数形结合地研究函数问题奠定了基础，图像法是研究和的重要方法。

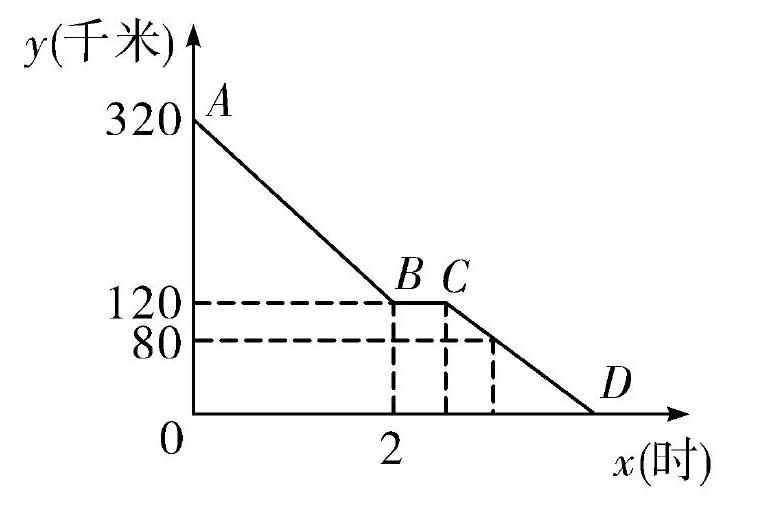
例：（2016陕西中考）上周六上午8点，小颖同爸爸妈妈一起从西安出发回安康看望姥姥，途中他们在一个服务区休息了半小时，然后直达姥姥家.如图，是小颖一家这次行程中距姥姥家的距离y（千米）与他们路途所用的时间x（时）之间的函数图象.

请你根据以上信息，解答下列问题：

（1）求线段AB所对应的函数关系式;

（2）已知小颖一家出服务区后，行驶30分钟时，距姥姥家还有80千米，问小颖一家当天几点到达姥姥家？

图中的三条线段就是对三个阶段的直观描述，读懂图中的信息是解决问题的关键，在教学中教会学生读图把图形用语言描述出来，及语言、图像、式三中表达方式的互换。通过数形、式形结合建立函数模型。图像的变化通过函数关系加以刻画，对于理解函数模型的价值具有重要意义。

1.3 基于实际问题中的数量关系建立函数模型

生活情景，为学生所熟悉。这类经济中的问题需要分析问题中的数量关系加量与量的关系，救助教学工具加以刻画。能否合理运用已有的思路和模式解决问题，是解决函数问题的基本策略。教师在教学中帮助学生形成认真勤奋、独立思考、合作交流、反思质疑等良好学习习惯。良好的学习习惯重点表现在良好的数学思维习惯的养成，及在新问题中合理运用已有的思考路径模式解决问题。

例.（2017陕西中考）某樱桃种植户有20吨樱桃待售，现有两种销售方式：一是批发，二是零售.经过市场调查，这两种销售方式对这个种植户而言，每天的销量及每吨所获的利润如下表：

假设该种植户售完20吨樱桃，共批发了x吨，所获总利润为y元.

（1）求出y与x之间的函数关系式;

（2）若受客观因素影响，这个种植戶每天只能采用一种销售方式销售，且正好10天销售完所有樱桃，请计算该种植户所获总利润是多少元？

实事上，这类问题的解决思路都是“选择方案”的问题，都是在学生在已有的函数模型经验的基础上解决问题。

建立不同形式的函数模型，是学生和教师解题经验的积累，教师在教学中要关注基础知识的落实，经验的积累，千题万题不如讲透一题，千法万发不如落实得法，教会学生通过学习、反思、总结内化为学生的知识与能力。

2 在函数建模教学实现学生知识、能力、素养的提升

建模是对现实生活问题的进行的数学抽象，用数学语言表达问题，用数学知识和方法构建模型，解决问题的过程。从这个意义讲函数建模是的函数知识和数学技能，也可理解成为函数学学习的过程。函数建模教学过程简化为三个环节：首先从现实生活或者具体情境中抽象出数学问题;然后，用数学符号建立函数表达变化关系。这一步中，学生要通过观察、分析、抽象、概括、选择、判断等数学活动完成模型抽象，这是建模最重要的一环。最后，通过函数模型求出结果，并用此结果解释讨论他在现实中的意义。

3 结语

总之，函数建模教学，学生要把实际问题简化、抽象为合理的一次函数模型。不仅需要教师在教学中以学生为中心，以问题为主线，以培养核心素养为目标;还需要调动学生学习数学的积极性，充分发挥学习的主动性，形成数学思维方式;为学生终身学习奠定基础，切实提升学生的数学素养。

（作者单位：陕西省镇安县回龙中学）