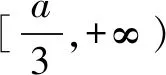解读函数“极值点”问题

梁宗明

(甘肃省兰州市兰化一中 730060)

函数在某个区间上“极值点”问题是近年来高考的常见题型，思路灵活、多样.学生理解、切入比较困难.总体而言题型大致分为四类：①至少有一个极值点；②当且仅当；③有且只有；④无极值点，只要区分清楚题目类型，配以相应的解决方案，问题就可以化难为简，迎刃而解.下面各举一例，从不同角度分析思路，希望给读者带来启发.

一、“至少有一个极值点”型

例1已知函数f(x)=x3-3ax2+3x+1在区间(2,3)中至少有一个极值点，求a的取值范围.

解析从不同角度等价解析：函数在区间上至少有一个极值点⟺函数在区间上不单调⟺导函数在区间上有零点.主要从导函数在区间上有零点突破.

思路一f′(x)=3x2-6ax+3,Δ=36(a2-1).

当Δ=36(a2-1)≤0时，f′(x)≥0恒成立，f(x)为增函数，故f(x)无极值点.问题转化为在Δ=36(a2-1)>0，即a<-1或a>1情形下，f′(x)=0在(2,3)有解，

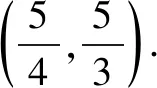
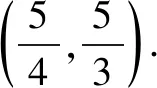
二、“当且仅当”型

例2已知函数f(x)=x5+ax3+bx+1,当且仅当x=±1是极值点，且极大值比极小值大4，(1)求a,b的取值；(2)求函数的极值.

解析当且仅当x=±1是极值点，说明函数只存在两个极值点，再无其他极值点，即便还有，必为“假”极值点.

因为f′(x)=5x4+3ax2+b，f′(±1)=0，解得b=-3a-5，当且仅当x=±1是极值点，所以f′(x)=(x+1)(x-1)(5x2+5+3a).令y=5x2+5+3a，则此函数必无极值点，或者为“假”极值点.所以Δ=-20(5+3a)≤0，即a≥-5/3，其余略解.

三、“有且只有”型

解析函数f(x)在区间(-1,1)中有且只有一个极值点，即f′(x)在区间(-1,1)中有且只有一个根，利用函数零点存在性定理直接求解.

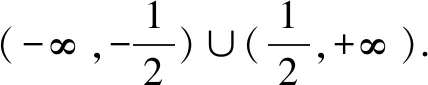
四、“无极值点”型

例4已知函数f(x)=x3+ax2-a2x+m(a>0)在区间[-1,1]上无极值点，求a的取值范围.

解析从不同角度等价解析：函数在区间[-1,1]无极值点⟺函数在区间[-1,1]上单调⟺f′(x)≥0或f′(x)≤0在区间上恒成立⟺导函数在区间[-1,1]上无解(即便有解，必为“假”极值点)⟺区间[-1,1]是函数单调区间的子区间.因为f′(x)=3x2+2ax-a2=(x+a)(3x-a)，依题f′(x)=0在区间[-1,1]上无解，又f′(0)=-a2，所以f′(-1)<0且f′(1)<0，解得a>3.