二重积分“以学定教”模式的研究
邱 云 兰
(广州工商学院,广州 510850)
一、问题提出
二重积分的计算和有关论证要注重有关理论的渗透与学法传授的针对性、灵活性、生成性、有效性。陶行知说:“教的法子就要根据学的法子。”以学的法子来设计教的内容和方法,教法的转变,是新一轮课程改革的重要目标和核心内容,也是课程改革的重点和难点。有的二重积分的计算或论证比较难,难在算量过大、情景过新、内容较深、交汇过强,因此,在课堂教学中要了解学情,以学定教,要静态地分析二重积分的概念、性质、公式的表述形式及其应用。梳理二重积分的知识体系,达到提升计算二重积分的能力。
二、二重积分的计算
二重积分的计算,一般可以利用直角坐标、极坐标、换元法、对称性等方法。根据题型特征选择解题方法,根据被积函数与积分区域选择恰当的坐标。虽然数学课程将不再强调是否向学生提供系统的数学知识,但“提倡算法多样化”。即通过“算法多样化”,能让学生站在系统的高度看问题,问题在数学中有举足轻重的作用,有问题学习才有动力,学生才会参与到整个学习过程中去。
1.直角坐标系中二重积分的计算
数学按知识点变识,一般有定义形式,命题变式,问题变式。在计算二重积分时,根据题型特征,灵活选择解法。有些要先将其变式,通过变式,选择解法利用坐标法计算。
解法1 首先要在直角坐标系中画出积分区D的图(图略),D是X—型的,D上以这个x值为横坐标的点在一段直线上,这段直线平行以y轴,该段直线上的纵坐标从y=0变到y=x。对y积分时,将x看作常数,再对x积分时,将y看作常数,积分区间D表示为
D={(x,y)│0x1,0yx},
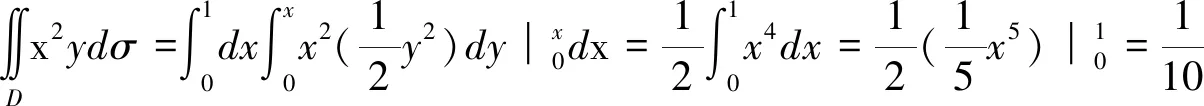
解法2 积分区D是Y—型的,D上的点的纵坐标的变化范围是区间[0,1],在区间[0,1]上任取一个y值,则在D上以这个y值的纵坐标的点在一段直线上,这段直线平行以x轴,该段直线上的横坐标从y=0变到y=x。对y积分时,将x看作常数,对x积分时,将y看作常数,积分区间D表示为
先对x积分时,将y看作常数,后对y积分时,将x看作常数。积分区间D表示为D={(x,y)│0y1,yx1},

2.极坐标系中二重积分的计算
有些二重积分,积分区域D的边界曲线用极坐标方程来表示比较简便,被积函数用极坐标变量ρ、θ表达比较简单。当积分区域或被积函数含有x2+y2的项时,用直角坐标计算不一定能计算出来。但是,用极坐标计算可能比较简便。极坐标系中的二重积分,也可化为二次积分计算。
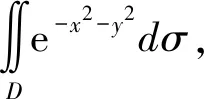
计算是一种实践能力,靠长期训练和积累,才能确保计算的准确性和快捷性。
3.利用对称性奇偶性计算二重积分
计算二重积分时要充分利用好积分区间的对称性和被积函数的奇偶性,这样可以减少积分运算。但要注意只有当积分区域D的对称性与被积函数的奇偶性满足时,才可以利用对称性定理。
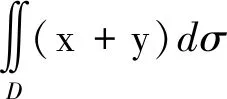
解 显然积分区域D关于x轴对称,故
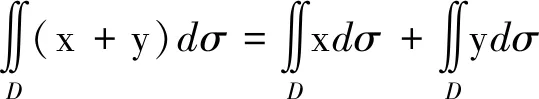
三、结语
计算二重积分的目的过程和实际价值的体现,在于提高教学质量和效益。二重积分是多元函数积分的一部分,二重积分的计算是化成二次积分。利用直角坐标计算二重积分时,要选好积分次序和确定积分限。利用极坐标计算二重积分要看极点是在区域D的外部还是外部,或边界,根据情况选择积分区间。一般说来,二次积分的个数较少,计算量就较小。有的二重积分要求交换积分次序计算二重积分,对这一类常见题型,关键是正确找出二重积分的区域D。根据区域及有关解题步骤计算;有的根据二重积分对称性定理,计算更简化,更简单。二重积分的定义、几何意义、性质及其计算公式等要融会贯通。教师要成为学生潜能贯通的合作者、“学好数学”的引路人,就必须“改变‘教师讲,学生听’‘教师问,学生答’‘教师写,学生记’的教学模式”,共同探索解题思路、解题过程、解题方法、解题规律,从而,促进数学知识的掌握和教学质量的提升。

