单参多极值点复解析多项式映射迭代函数系

陈 宁,关博文,海智刚

(沈阳建筑大学 信息与控制工程学院,沈阳 110168)

1 引 言

2 IFS定义与f(z)=zn+cz的数学特性

2.1 线性IFS的定义

平面上生成分形的迭代函数系(IFS),通常由两个或两个以上的线性仿射压缩变换组成.文献[4]给出了平面上IFS的定义:在欧氏空间(R2,ρE)上的一组线性压缩映射ωn:R2→R2,n=1,2,…,N,构成了一个IFS,其中:

ωn(x,y)=(anx+bny+en,cnx+dny+fn),n=1,2,…,N

(1)

式(1)中的(x,y)为平面上的点的横向和纵向坐标;an,bn,cn,dn,en,fn∈R1为实数.

文献[4]指出式(1)必须满足3个压缩条件:an2+cn2< 1,bn2+dn2< 1和an2+bn2+cn2+dn2<(andn-cnbn)2,才是一个可以生成分形的有效IFS.

在研究中笔者注意到:由于上述IFS中每个变换都是平面上的压缩变换,且每个压缩变换的吸引域都是除无穷远点外的整张平面,这些变换在动力平面上的公共吸引域与IFS中单个变换的吸引域相同.因此,IFS的分形或其近似分形可以通过选取平面上的任意有界闭集作为初始迭代集,也可以从平面上的任意有界点作为初始迭代点,通过随机迭代得到分形或其近似值.

2.2 复映射f(z)=zn+cz的数学特性

动力平面上的原点(0,0)是复映射族f(z)=zn+cz的不动点.由于复映射的1阶导数为f′(z)=nzn-1+c,所以,当|c|<1时,点(0,0)是复映射的吸引不动点;当|c|>1时,点(0,0)是复映射的排斥不动点.如果该映射当|c|>1时有非零不动点f(pj)=pj,则取:

(2)

使:

即复映射f(z)=zn+cz有n-1个旋转对称不动点.由于动力平面上的复映射f(z)=zn+cz的极值点zc为其1阶导数为0的点,使f′(zc)=0,有:

(3)

式(3)表明,与复映射f(z)=zn+c只有1个极值点不同,复映射f(z)=zn+cz在动力平面上有n-1个旋转对称的极值点.

3 复映射f(z)=zn+cz的M集与充满Julia集

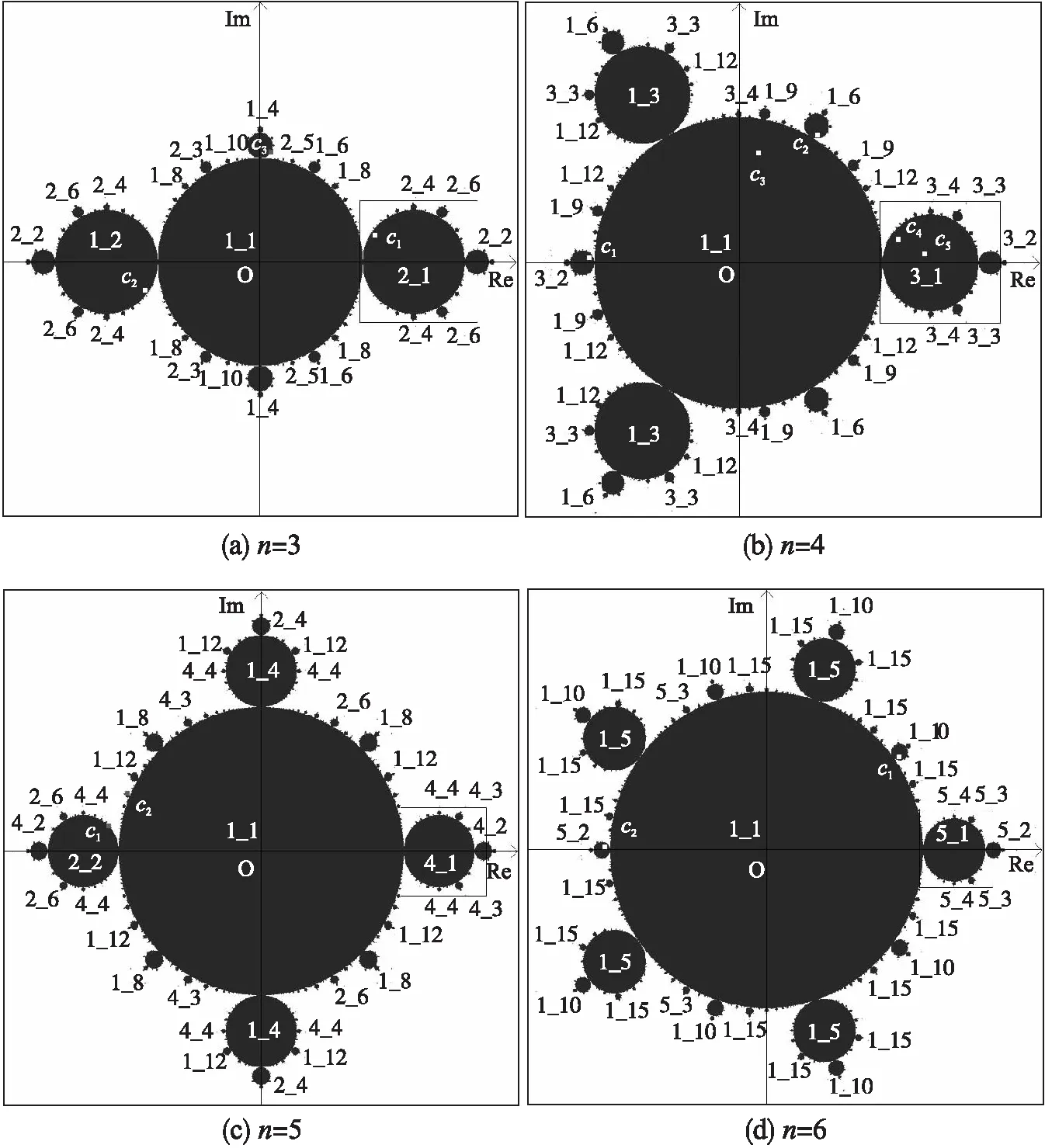
图1 复映射族f(z)=zn+cz的M集Fig.1 M sets of the complex mapping family of f(z)=zn+cz

易于证明复映射族f(z)=zn+cz在动力平面上是n-1旋转对称的,因此,相应的充满Julia集在动力平面上也是n-1旋转对称的.图2说明在图1的M集各图中取参数构造出的充满Julia集图形是在原点处分叉的.复映射族f(z)=zn+cz的充满Julia集图形结构与参数在M集上的几何对称位置有关.虽然对称位置上参数的迭代映射的吸引周期轨道条数不同,但吸引周期点的“总和”p相同,所以,这些参数下的充满Julia集除了相差旋转角度以外,他们的充满Julia集的图形结构是完全相同的,如图2(a)与图2(b)、图2(d)与图2(e)以及图2(h)与图2(i)所示.在复映射族f(z)=zn+czM集的芽苞上的芽苞区域选取参数c,相应的充满Julia集有多级分叉结构,如图2(c)与图2(f)所示.图2(g)是M集上A序列周期芽苞参数的充满Julia集.

在图1所表示的复映射族f(z)=zn+cz的每一个M集中,均有2个1周期参数区域:1个是以原点为中心的“1_1”参数区域,另一个是中心在正实轴上的“(n-1)_1”参数区域.由构造M集时参数区域的标记方法可知,采用1_1区域中参数c构造的迭代映射,在动力平面上只有1个吸引周期不动点,通过式(3)计算的(n-1)个极值点的轨道都到达原点(0,0).由前面讨论得到1_1区域中的参数|c|<1,且充满Julia集的几何特点是包含原点在内的并以原点为中心的(n-1)旋转对称实心区域.图3(a)表示了n=4时,在图1bM集的1_1区域取参数c3时,动力平面上的充满Julia集,以及根据式(3)计算出的3个极值点迭代到吸引不动点(0,0)的轨道,充满Julia集的几何特点是以原点为中心的3旋转对称实心结构.

如果在正实轴上的“(n-1)_1”芽苞区域选取参数c构造迭代映射f(z)=zn+cz,这个区域中参数下的映射在动力平面上有(n-1)个旋转对称分布的1周期吸引不动点(pj,j=0,1,2,…,n-2),可以通过式(2)直接计算得到,也可以通过式(3)的(n-1)个旋转对称分布的极值点(zcj,j=0,1,…,n-2)的迭代得到(如图3(b)和图3(c)所示).(n-1)个吸引不动点在动力平面上有(n-1)个旋转对称分布的吸引域,形成在原点处有(n-1)个旋转对称分叉的充满 Julia集图形结构.由于这个参数区域的参数模值大于1,所以原点是这个迭代映射的斥性不动点,是充满Julia集的边界上的(n-1)个旋转对称分布吸引域的边界的交点.图3(b)和图3(c)分别为取自图1(b)中的n=4 M集的3_1周期芽苞上的参数c4和c5的迭代映射在动力平面上的充满Julia集图形,3种颜色分别代表迭代映射的3个吸引不动点的吸引域,每个吸引域上给出了极值点zcj、吸引不动点pj以及从zcj到pj的迭代轨道.

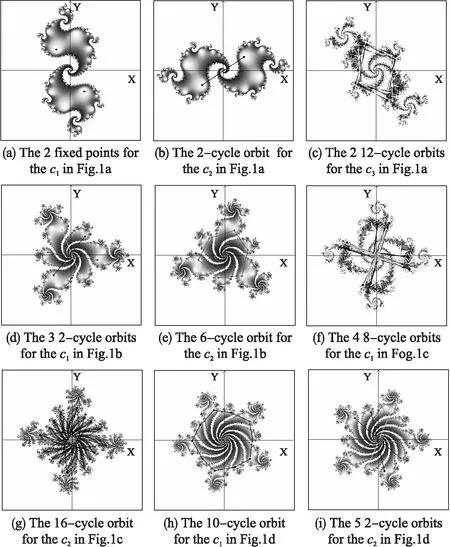
图2 复映射f(z)=zn+cz的充满Julia集及其轨道Fig.2 Filled-in Julia sets and the orbits of f(z)=zn+cz

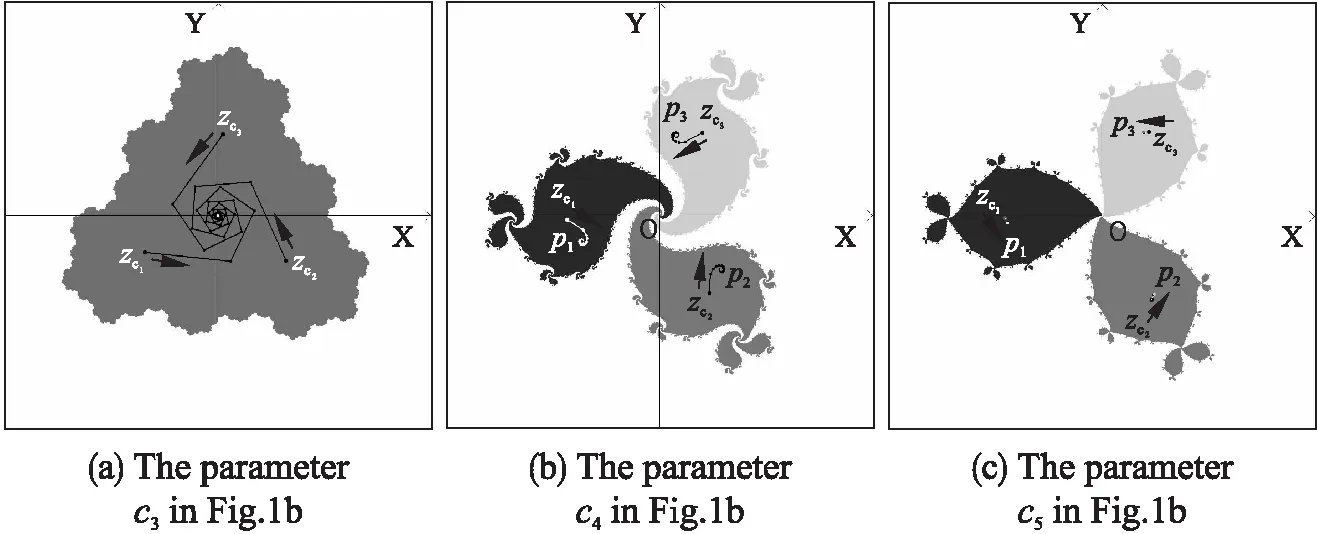
图3 在复映射f(z)=z4+cz M集的″1_1″与″3_1″周期芽苞区域中选取参数生成的充满Julia集及3个极值点的迭代轨道、吸引不动点Fig.3 Filled-in Julia set, 3 iterating orbits and 3 attracting fixed points respectively from the 3 parameters chosen from the ″1_1″and″3_1″cycle bud regions of the M set of f(z)=z4+cz

4 构造复映射族 f(z)=zn+cz IFS及分形

如前所述,复映射族f(z)=zn+cz的M集上有2个可以构造具有吸引不动点迭代映射的参数区域“1_1”和“(n-1)_1”,但是可以构造分形的有效IFS的参数区域是“(n-1)_1”.虽然在“1_1”参数区域选取参数可以在动力平面上构造出具有吸引不动点的充满Julia集,但是如果在“1_1”参数区域选取N个参数构造IFS,由于IFS中的所有N个迭代映射的吸引不动点都是原点(0,0),而且原点是复映射族f(z)=zn+cz的零点,所以无论怎样随机挑选IFS中的迭代映射去迭代吸引不动点(0,0),迭代轨道永远停留在原点(0,0)处,即M集的“1_1”参数区域不能用于有效构造IFS.

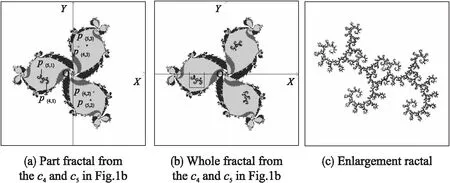
图4 在复映射f(z)=z4+cz的M集的3_1芽苞区域选参数构造分形Fig.4 Construction of the fractal from f(z)=z4+cz with the parameters chosen on the 3_1 cycle bud region in the M set

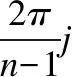
图5是n=3,4,5,6时,放大图1中的各“(n_1)_1”芽苞参数区域的M集图形.图6是采用上述算法,分别由图5中各图的参数且N=2或3或4时,由复映射f(z)=zn+cz构造的非线性IFS的n-1旋转对称分形图的一个旋转对称部分的放大分形图.

图5 复映射族f(z)=zn+cz M集的(n-1)_1芽苞区域放大图Fig.5 Enlargement of the (n-1)_1 cycle bud region of the M sets of f(z)=zn+cz

5 结 语

单参复映射族f(z)=zn+cz具有(n-1)个极值点,在参数平面上的M集由考察参数下相应迭代映射的(n-1)个极值点的迭代轨道有界构造.用符号 “number1_number2”表示M集1个周期芽苞参数区域中的所有参数都可以在动力平面上构造出具有number1条number2吸引周期轨道的迭代映射.

该映射族的M集在对称位置参数下的迭代映射在动力平面上的动力学特性可以不同,但是这些迭代映射所有吸引周期轨道的吸引周期点的“总和”相同,其充满Julia集图形结构相同.

图6 来自复映射族f(z)=zn+cz的分形Fig.6 Fractals from the f(z)=zn+cz

该映射族在n≥3时的M集中有2个1周期参数区域:包含原点(0,0)的单位圆区域“1_1”和正实轴上的单位圆外的区域“(n_1)_1”.

由于“1_1”区域中的参数|c|<1,相应迭代映射的(n-1)个极值点的迭代轨道都被吸引不动点(0,0)吸引,所以,在这个区域选取N(N≥2)个参数构造不出有效的IFS.

如果在“(n_1)_1”参数区域选取N个参数构造迭代映射,由于|c|>1,原点(0,0)退化成斥性不动点,而(n-1)个极值点的迭代轨道被(n-1)个旋转对称分布的吸引不动点吸引,所以,N个迭代映射的充满Julia集均是以原点(0,0)为交汇点的(n-1)个旋转对称分叉图形.如果N个迭代映射的N(n-1)个吸引不动点在N个充满Julia集的公共吸引域X内,则N个迭代映射构成了非线性IFS:{X,f(z)=zn+ciz,i=1,2,…,N}.

利用本文提出的双随机迭代法可以大量构造来自于复映射族f(z)=zn+cz的具有(n-1)旋转对称分形.